Metric and Time Conversions

ATI Launch 2025

Metric System

• most common measurement used in nursing

• beneficial bc it allows nurses to covert weight into volume

Metric System Key Points

• Base units of measurement

• Metric prefixes 

• Uses powers of 10

• Only written as whole numbers or decimals

Base Units

In the metric system, 3 base units are recognized for various measurements.

• Liter (L) is the base unit for volume

• Gram (g) is the base unit for weight

• Meter (m) is the base unit for length

Metric Prefixes

Metric base units are proceeded by prefixes, each associated with a specific value. The prefixes include kilo-, hecto-, deca-, base, deci-, centi-, milli-, decimilli-, centimilli-, and micro-. Nurses commonly use kilo-, centi-, milli-, and micro-. 

Prefixes above the base are factors of the base unit, whereas prefixes below the base are decimals.

Metric System

Prefix	Value
Kilo -	1000
Hecto -	100
​​​​​​​Deca -	10
​​​​​​​Base	0
Deci -	0.1
Centi -	0.01
Milli -	0.001
Decimilli -	0.0001
Centimilli -	0.00001
Micro -	0.000001

To remember metric system prefixes, memorize this mnemonic.

King Henry Died Drinking Chocolate Milk

Metric System Conversions

Math calculations may require conversions within the metric system to move from one prefix to another prefix. For example, nurses must convert a newborn’s weight from kilograms to grams to have a more specific measurement to document. There are a variety of approaches you can take to convert measurements. One approach is using basic math principles like multiplication and division. Another approach is to move the decimal point to the left or right.

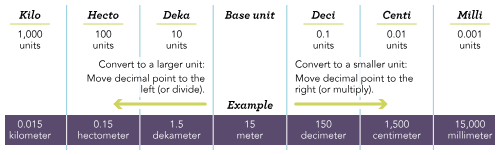
Converting Larger Units to Smaller Units (Kilograms to Milligrams)

When converting from a larger unit to a smaller unit, move the decimal to the right. Multiply by multiples of 10 with each unit change.

 Example: convert 1 kilogram to milligrams

Kilograms and milligrams are 6 positions apart. Move the decimal point 6 places to the right. The result equals 1000000 (10⁶).

1 kilogram x 1000000 = 1000000 milligrams

When converting from a larger unit to a smaller unit, move the decimal to the right. Multiply by multiples of 10 with each unit change.

 ​​​​​​​Example: convert 1 kilogram to decagrams

Kilograms and decagrams are 2 positions apart. You should move the decimal 2 places to the right.

If you move 1.0 kilogram 2 places to the right it equals 100 decagrams

Converting Smaller Units to Larger Units (Milligrams to Kilograms)

When converting from a smaller unit to a larger unit, divide by multiples of 10 with each unit change.

             Example: convert 1000 milligrams to grams

            Milligrams and grams are 3 positions apart. Move the decimal three places to the left. The result is 1000 (10³).

            1000 milligrams ÷ 1000 = 1 gram

When converting from a smaller unit to a larger unit, move the decimal to the left.

           ​​​​​​​  Example: convert 1000 grams to kilograms

            Grams and kilograms are 3 positions apart. Move the decimal 3 places to the left.

            To convert 1000.0 grams to kilograms, move the decimal 3 places to the left. The result is 1 kilogram.

            1000 grams = 1 kilogram

Household System

The household measurement system is commonly used in the home setting. This system of measurement uses cooking measurement devices like measuring spoons and cups.

• Common units of measurement include teaspoon (tsp), tablespoon (Tbsp), ounce, cup, pint, and quart.

• The household system uses whole numbers and fractions to express measurements instead of decimals.

• Although a familiar system of measurement, the household system is considered the least accurate and not recommended for medication administration. Measurements are often inaccurate because each measurement (teaspoon, cup) varies slightly in its standardized size.

• To ensure a more accurate measurement, nurses should use calibrated syringes and medicine cups when administering medications.

Volume

Volume is the amount or quantity of something.

Nurses commonly calculate the volume of a liquid.

• Nurses measure volume when they calculate medication doses, fluid intake, urinary output, intravenous (IV) fluids, and more.

Nurses measure volumes using the metric system because metric system is more accurate than the household system. ​​​​​​​

The metric base unit for volume is the liter (L). The liter is most commonly used when measuring IV fluids.

IV Fluid Bag

This IV fluid bag contains 1 liter or 1000 milliliters (mL).

Nurses commonly convert this unit of measurement.

*The prefix milli- on milliliter represents one-thousandth of 1 liter. Milliliters are commonly used to measure medication dosages and intake or output.

Match the abbreviation with its metric unit.

g - gram

mL - milliliter

kg - kilogram

L - liter

mcg - microgram

A liter is the metric base unit for volume, abbreviated as L. Milliliter is one-thousandth of a liter, abbreviated as mL. Gram is the metric base unit for weight, abbreviated as g. Microgram is one-millionth of a gram, abbreviated as mcg. Kilogram is 1000 grams, abbreviated as kg. 

Volume Equivalencies

Nurses commonly use the household system to determine a client’s liquid intake and to educate a client about a specific amount of liquid intake.

However, the household system should be avoided when measuring medications due to the system’s lack of accuracy.

Because household measurements are used by clients, nurses must remember the equivalencies between household and metric systems to calculate conversions.

Measurement Equivalencies

Teaspoons (tsp)	Tablespoons (Tbsp)	Milliliters (mL)	Ounces (oz)	Cups (C)	Pints (pt)	Quarts (qt)
1 tsp	____	5 mL	____	____	____	____
3 tsp	1 Tbsp	15 mL	____	____	____	____
6 tsp	2 Tbsp	30 mL	1 oz	1/8 C	____	____
48 tsp	16 Tbsp	240 mL	8 oz	1 C	1/2 pt	1/4 qt
96 tsp	32 Tbsp	480 mL	16 oz	2 C	1 pt	1/2 qt
192 tsp	64 Tbsp	960 mL	32 oz	4 C	2 pt	1 qt

Match the measurement with its equivalent measurement.

2 C - 480 mL

8 oz - 1 C

1 Tbsp - 15 mL

5 mL - 1 tsp

1 oz - 30 mL

Household To Metric Conversions

Household-to-metric conversions can be done using calculation methods including ratio-proportion, dimensional analysis, and desired over have.

*Prior to performing a calculation, fractions must be converted into decimals.

Ratio-Proportion Method

Convert 3/4 C to mL.

​​​​​​​Convert the fraction to a decimal first.

Step 1: Divide the numerator by the denominator.

3  ÷  4  =  0.75  C​​​​​​​

Step 2: What unit of measurement is required?

mL

Step 3: Set up a proportion and solve for x.

Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

1  C / 240  mL  =  0.75  C / x  mL

​1x  =  240  ×  0.75

1x = 180

1x  ÷  1  =  180  ÷  11

x = 180mL

Dimensional Analysis Method

Convert 3/4 C to mL.

Convert the fraction to a decimal first.

Step 1: Divide the numerator by the denominator.

3  ÷  4  =  0.75 C​​​​​​​

Step 2: What unit of measurement is needed? (Place the unit of measurement needed on the left side of the equation).

x  mL  =

Step 3: Find the ratio of the item that contains the same unit as the unit calculated. (Place the ratio on the right side of the equation, ensuring that the unit in the numerator matches the unit being calculated).

xmL = 240mL / 1 C​​​​​​​​

 

Step 4: Place any remaining ratios that are relevant to the item on the right side of the equation, along with any necessary conversion factors to cancel out unwanted units of measurement.

x  mL  =  240  mL / 1  C  ×  0.75  C / 1 ​​​​​​​​

 

Step 5: Solve for x (multiply across the equation and divide the numerator by the denominator).

x  mL  =  180  mL​​​​​​​

Step 6: Round if necessary.

 

Step 7: Determine if the amount makes sense.

If there are 240 mL in 1 C, it makes sense that 180 mL is equivalent to 3/4​​​​​​​ of a cup.

Desired Over Have Method

Convert 3/4 C to mL.

Convert the fraction to a decimal first.

Step 1: Divide the numerator by the denominator.

3  ÷  4  =  0.75  C

Step 2: What is unit of measurement needed?

mL

Step 3: Set up an equation to solve for x.

x  mL  =  0.75  C  ×  240  mL / 1  C​

 

Step 4: Solve for x.

x  =  180  mL

 

Step 5: Determine if the amount makes sense. 

If there are 240 mL in 1 C, it makes sense that 180 mL is equivalent to 3/4 of a cup.

When solving for a household measurement, the final answer should be expressed as a fraction if it is in decimal form. When solving for a metric measurement, the final answer should be expressed as a decimal.

Case Study #2: Nurse: We must determine how much water a client has consumed with their meal.

Student Nurse: The client reports drinking 3 1/2 ​​​​​​​​ cups of water with their meal.

Nurse: We will need to convert cups to milliliters in order to document how much water the client consumes in their record.

A client reports drinking 3 ½ ​​​​​​​​ cups of water. How many milliliters of water should the student nurse document in the client’s record?

840 mL

A client reports drinking 6 ounces of coffee. How many cups did the client drink?

¾ cups

Ratio and Proportion Method

Step 1: What is the unit of measurement needed?C

​​​​​​​Step 2: Set up a proportion and solve for x.

Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

8  oz / 1  C  =  6  oz x  C

​​​​​​​​8  ×  x  =  6  ×  1

8×x=6×1​​​​​​

8x  =  6

​​​​​​8x  ÷  8  =  6  ÷  8

​​​​​​​x  =  6/8  =  ¾ C

​​​​​​​​​​​​​​Note: When solving for a household measurement, the final answer should be expressed as a fraction. Reduce the fraction if necessary.

Dimensional Analysis Method

Step 1: What unit of measurement should the nurse calculate? Place the unit of measurement being calculated on the left side of the equation.

x  C  = ​​​​​​​​​​​​​​​​​​​​​

Step 2: Find the ratio of the item that contains the same unit as the unit being calculated. Place the ratio on the right side of the equation, ensuring that the unit in the numerator matches the unit being calculated.

x  C  =  8  oz / 1  C​

Step 3: Place any remaining ratios that are relevant on the right side of the equation along with any necessary conversion factors to cancel out unwanted units of measurement.

x  C  =  1  C8  oz  ×  6  oz1xC=8oz1C​×16oz​​​​​​​​

Step 4: Solve for x (multiply across the equation and divide the numerator by the denominator).x  C  =  68  =  34CxC=86​=43​C

​​​​​​​Step 5: Round if necessary.

Step 6: Determine if the amount to give makes sense.

If there are 8 oz in 1 C, it makes sense that 6 oz is equivalent to 3/4 of a cup.

Note: When solving for a household measurement, the final answer should be expressed as a fraction. Reduce the fraction if necessary.

Desired Over Have Method

Step 1: What is the unit of measurement required?

CCStep 2: Set up an equation to solve for x.

x  C  =  6  oz  ×  1  C8  oz

​Step 3: Solve for x.

x  C  =  6/8  =  3/4C

​​​​​​​Step 4: Determine if the amount makes sense.

If there are 8 oz in 1 C, it makes sense that 6 oz is equivalent to 3/4​​​​​​​ of a cup.

Note: When solving for a household measurement, the final answer should be expressed as a fraction. Reduce the fraction if necessary.

A nurse cares for a client who is prescribed 75 milliliters of a medication once a day. How many tablespoons should the nurse administer?

5 tbsp

Ratio and Proportion Method

Step 1: What is the unit of measurement needed?

Tbsp

Step 2: Set up a proportion and solve for x.

Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

1  Tbsp / 15  mL  =  x  Tbsp / 75  mL

​​​​​​​​1  ×  75  =  15  ×  x

75=15×

​​​​​​​​​​75  ÷  15  =  15x  ÷  15

​​​​​​​x  Tbsp  =  5

A provider prescribes a client 300 mcg of a medication to take by mouth daily at bedtime. The available dose is 0.1 mg/tablet. How many tablets should the nurse administer?

3 tablets

Ratio and Proportion

Step 1: What is the unit of measurement the nurse should calculate?

tablet(s)

Step 2: What is the desired dose?

200 mcg

Step 3: What is the dose available?

1 mg

Step 4: Convert units of measurement if necessary. Milligrams does not equal micrograms.

1,000  mcg /1  mg  =  300  mcg / x  mg

1000 x / 1000 = 300mcg / ​1,000 

​x  mg  =  0.3  mg​​​​​​​

Step 5: What is the quantity of the dose available?

1 tablet

Step 6: Set up an equation and solve for x

To solve, cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Division is the final step to solving the equation.

Have / Quantity  =  Desired / x  tablet(s)

=  0.3  mg / x  tablet(s)=

​      0.1         0.1  x / 0.1  =  0.3  mg/ 0.1

​x  tablet(s)  =  3  tablets​​​​​​​

Step 7: Round if necessary.

Step 8: Determine if the amount to administer makes sense.

If there is 0.1 mg in 1 tablet and the amount prescribed is 300 mcg (0.3 mg), it makes sense to administer 3 tablets. The nurse should administer 3 tablets by mouth daily at bedtime.

Length

A measurement from a starting point to an ending point.

• When measuring the length of a client’s wound, the nurse should measure the distance from one point of the wound to the another point.

  • the metric base unit for length is the meter (m). Nurses use forms of the meter—the centimeter (cm) and the millimeter (mm)—the most.

Height

A measurement of a client or object vertically.

When measuring a client’s height, the nurse should measure from the client’s head to the client’s feet.

• the metric base unit for height is the meter (m). Nurses use forms of the meter—the centimeter (cm) and the millimeter (mm)—the most.

*Volume, length, and height are measured using the metric system to provide the most accurate results.

Measuring the Length of a Newborn

The prefix centi- on centimeter represents one-hundredth of 1 meter. Centimeters are commonly used in nursing to measure wounds, body surface area, and newborn length.

Pupil Size Measurements

The prefix milli- on millimeter represents one-thousandth of 1 meter. Nurses commonly use millimeters to measure a client’s pupil size and skin lesions.

A client has a mass measuring 16.4 cm wide. How many mm wide is the mass?

164 mm

When converting a larger unit to a smaller unit, multiply by multiples of 10 with each unit change.

16.4 cm to mm

Centimeters and millimeters are 1 position apart. Move the decimal point 1 place to the right. This is equivalent to 10 (10¹).

16.4 centimeters x 10 = 164 millimeters

When converting from a larger unit to a smaller unit, the decimal moves to the right.

16.4 cm to mm

Centimeters and millimeters are 1 position apart. Move the decimal 1 place to the right.

If you move the decimal point 1 place to the right, 16.4 cm becomes 164 mm.

A client has a skin lesion measuring 104 mm in length. What is the length of the skin lesion in cm?

10.4 cm

When converting a smaller unit to a larger unit, divide by multiples of 10 with each unit change.

104 mm to cm

Millimeters and centimeters are 1 position apart. Move the decimal point 1 place to the left which is equivalent to 10 (10¹).

104 mm ÷ 10 = 10.4 cm

When converting from a smaller unit to a larger unit, the decimal moves to the left.

104 mm to cm

Millimeters and centimeters are 1 position apart. Move the decimal point to the left.

If you move the decimal point 1 place to the left, 104 mm becomes 10.4 cm.

Height and Length Equivalencies

Households use household measurements for height and length frequently. However, in nursing, the metric system is the preferred choice of measurement. - Household units for height and length include inches, feet, and yards.

To calculate accurate measurements, nurses must be able to convert household measurements to metric measurements.

Because household measurements are still used by clients, nurses must remember the conversions between household and metric systems.

Measurement Equivalencies

Measurement Equivalencies

Millimeters (mm)	Centimeters (cm)	Inches	Feet	Yard
10 mm	1 cm	____	____	____
25.4 mm	2.54 cm	1 in	____	____
304.8 mm	30.48 cm	12 in	1 ft	____
914.4 mm	91.44 cm	36 in	3 ft	1 yd

Household to Metric Conversions

Household-to-metric conversions can be done using calculation methods (ratio-proportion, dimensional analysis, desired over have).

Ratio and Proportion Method

Convert 16 inches to centimeters.

Step 1: What is the unit of measurement required?

cm

Step 2: Set up a proportion and solve for x.

Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation).​​​​​​​

​​​​​​​1  inch / 2.54  cm  =  16  inches / x  cm

​​​​​​1x  =  2.54  ×  16

​​​​​​​1x  =  40.64

​​​​​​​​​​​​​​1x  ÷  1  =  40.64  ÷  1

​​​​​​​x  =  40.64 cm​

Dimensional Analysis Method

Convert 16 inches to centimeters.

Step 1: What unit of measurement should the nurse should calculate? Place the unit of measurement being calculated on the left side of the equation.

x  cm  =​​​​​​​

Step 2: Find the ratio of the item that contains the same unit as the unit being calculated. Place the ratio on the right side of the equation, ensuring that the unit in the numerator matches the unit being calculated.

x  cm  =  2.54  cm /1  inch​

​​​​​​​Step 3: Place any remaining ratios that are relevant to the item on the right side of the equation along with any necessary conversion factors to cancel out unwanted units of measurement.

x  cm  =  2.54  cm / 1  inch  ×  16  inches/ 1

​​​​​​​​Step 4: Solve for x (multiply across the equation and divide the numerator by the denominator).

x  cm  =  40.64

​​​​​​​Step 5: Round if necessary.

Step 6: Determine if the amount to give makes sense.

If there are 2.54 cm in 1 inch, it makes sense that 40.64 cm is equivalent to 16 inches.

Desired Over Have Method

Convert 16 inches to centimeters.

Step 1: What is the unit of measurement needed?

cm

Step 2: Set up an equation to solve for x.

x  cm  =  16  inches  ×  2.54  cm / 1  inch​​​​​​​​

Step 3: Solve for x.

x  =  40.64  cm

​​​​​​​Step 4: Determine if the amount to give makes sense.

If there are 2.54 cm in 1 inch, it makes sense that 40.64 cm is equivalent to 16 inches.

A nurse cares for a client who is 6 feet tall. How tall is the client in inches?

72 inches

Ratio and Proportion Method

Step 1: What is the unit of measurement required?

inches

Step 2: Set up a proportion and solve for x.

Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

12  inches  1  foot=x  inches  6  feet​​​​​​
​​​​​​​​​​​​​1x=12×6

1x=72​​​​​​​
​​​​​​​​​​​​
​​​​​​
1x÷1=72÷1​​​​​​​
​​​​​​​
x=72  inches​​​​​​​​​​​​​​

Dimensional Analysis Method

Step 1: What unit of measurement should the nurse calculate? Place the unit of measurement being calculated on the left side of the equation.

x  inches= ​​​​​​​

​​​​​​​Step 2: Find the ratio of the item that contains the same unit as the unit being calculated. Place the ratio on the right side of the equation, ensuring that the unit in the numerator matches the unit being calculated.

x  inches= 1  foot  12  inches​​​​​​​

Step 3: Place any remaining ratios that are relevant on the right side of the equation along with any necessary conversion factors to cancel out unwanted units of measurement.

​​​​​​​x  inches= 1   feet  12  inches×16 feet​​​​​​​​​​​​​​
 
Step 4: Solve for x (multiply across the equation and divide the numerator by the denominator).

x  inches=72​​​​​​​

​​​​​​​Step 5: Round if necessary.

Step 6: Determine if the amount makes sense.

If there are 12 inches in 1 foot, it makes sense that 72 inches is equivalent to 6 feet.

Desired Over Have Method

Step 1: What is the unit of measurement required?

inches

Step 2: Set up an equation to solve for x.

x  in= 1 foot  6 feet×12  inches​​​​​​​

Step 3: Solve for x.

x=72  inchesx​​​​​​​

Step 4: Determine if the amount makes sense.

If there are 12 inches in 1 foot, it makes sense that 72 inches is equivalent to 6 feet. 

Case Study #3: Nurse: A new client arrived for admission. We must record their height before they get in bed.

Student Nurse: The client’s height is 5 feet 4 inches. I will document the client’s height in their medical record.

Nurse: Don’t forget—we must convert the height from feet and inches to centimeters. 

A student nurse cares for a client whose height is 5 feet 4 inches. How tall is the client in centimeters? 

162. 56 cm → rounded to 162.6 cm

Calculating this problem requires the following two conversions: feet and inches to inches and then inches to centimeters.

Ratio and Proportion Method

​​​​​​​Step 1: What is the unit of measurement needed?

inches

Step 2: Set up a proportion and solve for x.

Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

1  foot / 12  inches  =  5  feet / x  inches

​​​​​​​​1x  =  12  ×  5

​​​​​​​​​​​​​​​1x  =  60

​​​​​​​1x  ÷  1  =  60  ÷  1

​​​​​​x  =  60  inches

​​​​​​​Step 3: Add remaining inches.

60  +  4  =  64  inches​​​​​​​

Convert Inches to Centimeters

Step 1: What is the unit of measurement required?

cm

Step 2: Set up a proportion and solve for x.

Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

1  inch / 2.54  cm  =  64  inches / x  cm

​​​​​​​​1x  =  2.54  ×  64

​​​​​​​​​​​​​​​1x  =  162.56

​​​​​​1x  ÷  1  =  162.56  ÷  1

​​​​​​​x  =  162.56  cm

 

Dimensional Analysis Method

Step 1: What unit of measurement should the nurse calculate? Place the unit of measurement being calculated on the left side of the equation.

x  inch  =

​​​​​​​Step 2: Find the ratio of the item that contains the same unit as the unit being calculated. Place the ratio on the right side of the equation, ensuring that the unit in the numerator matches the unit being calculated.

x  inches  =  12  inches / 1  foot

​​​​​​​​Step 3: Place any remaining ratios that are relevant on the right side of the equation along with any necessary conversion factors to cancel out unwanted units of measurement.

​​​​​​​x  inches  =  12  inches / 1  foot  ×  5  feet / 1

​​​​​​​​​​​​​​​​​​​​​​Step 4: Solve for x (multiply across the equation and divide the numerator by the denominator).

x  inches  =  60

​​​​​​Step 5: Add remaining inches.

60  +  4  =  64  inches

​​​​​​​Step 6: Round if necessary.

Step 7: Determine if the amount to give makes sense.

If there are 12 inches in 1 foot, it makes sense that 64 inches are equivalent to 5 feet 4 inches.

Convert Inches to Centimeters

Step 1: What unit of measurement should the nurse should calculate? (Place the unit of measure being calculated on the left side of the equation).

x  cm  =​

​​​​​​Step 2: Find the ratio of the item that contains the same unit as the unit being calculated. (Place the ratio on the right side of the equation, ensuring that the unit in the numerator matches the unit being calculated).

x  cm  =  2.54  cm / 1  inch

​​​​​​​​Step 3: Place any remaining ratios that are relevant on the right side of the equation along with any necessary conversion factors to cancel out unwanted units of measurement.

x  cm  =  2.54  cm/ 1  inch  ×  64  inches / 1

​​​​​​​​Step 4: Solve for x (multiply across the equation and divide the numerator by the denominator).

x  cm  =  162.56  

​​​​​​Step 5: Round if necessary.

Step 6: Determine if the amount makes sense.

If there are 2.54 cm in 1 inch, it makes sense that 162.56 cm is equivalent to 64 inches.

Desired Over Have Method

Step 1: What is the unit of measurement required?

inches

Step 2: Set up an equation to solve for x.

x  inches  =  5  feet  ×  12  inches / 1  foot

​​​​​​​​Step 3: Solve for x.

x  =  60  inches

​​​​​​​Step 4: Determine if the amount to give makes sense.

If there are 12 inches in 1 foot, it makes sense that 60 inches is equivalent to 5 feet.

Step 5: Add remaining inches.

60  +  4  =  64  inches

​​​​​ Convert Inches to Centimeters

 Step 1: What is the unit of measurement needed?

cm

Step 2: Set up an equation to solve for x.

x  cm  =  64  inches  ×  2.54  cm / 1  inch

​​​​​​​​Step 3: Solve for x.

x  =  162.56  cm​​​​​​​

Step 4: Determine if the amount makes sense.

If there are 2.54 cm in 1 inch, it makes sense that 162.56 cm is equivalent to 64 inches.

Weight

Many medications are prescribed by weight, especially in the pediatric population and in critical care.

It is important to accurately weigh clients to ensure that overdosing or underdosing does not occur.

Many medication dosages are based on milligrams or micrograms per kilogram. Therefore, knowledge of conversion from pounds and ounces to kilograms will help with calculating and administering medications accurately and safely to clients.

When converting between units of measurement, remember the following equivalents for weight:

1 kg = 2.2 lb

1 lb = 16 oz

Case Study #5: Nurse: A baby was just born in the labor and delivery unit. Let’s get the baby’s weight!

Student Nurse: The baby weighs 6 lb, 14 oz. I’ll document the weight in their medical record.

Nurse: Remember, first, we must convert the weight from pounds to kilograms.

 A student nurse cares for an infant who weighs 6 lb 14 oz. How much does the infant weigh in kilograms? Round to the nearest tenth.

3.1 kg

Ratio and Proportion

First, determine the client’s weight in pounds.

Step 1: What is the unit of measurement needed?

lb

Step 2: Set up an equation and solve for x

To solve, cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

16  oz / 1  lb  =  Weight  oz/ x  lb

​​​​​​​​16  oz /1  lb  =  14  oz / x  lb

​​​​​​​​16x / 16  =  14 / 16​​​​​​​​

x  lb  =  0.875  lbxlb=0.875lb​​​​​​​

Step 3: Add the remaining weight.

6  lb  +  0.875  =  6.875  lb ​​​​​​

 

Next, determine the client’s weight in kilograms.

Step 1: What is the unit of measurement needed?

kg

Step 2: Set up an equation and solve for x.

To solve, cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Divide to solve the equation.

2.2  lb / 1  kg  =  lb /x  kg

2.2lb / 1kg  =  6.875  lb / x  kg

​​​​​​​​2.2  x / 2.2  =  6.875 / 2.2​​​​​​​

x  kg  =  3.125  kg​​​​​​​

Step 3: Round if necessary.

3.125 rounds to 3.1

Step 4: Determine if the equivalent makes sense.

If 2.2 lb is equivalent to 1 kg, it makes sense that 6.875 lb is equivalent to 3.1 kg.​​​​​​​

A nurse admits a new client to the unit. The client weighs 155 lb. What is the client’s weight in kilograms? Round to the nearest tenth.

70.5

Body Temperature

A measurement of the degree of heat in the human body.

An alteration in a client’s temperature could indicate a change in their body.

• For example, an elevated temperature could indicate that a client is experiencing an infection.

How is temperature monitored?

Temperature is monitored using the Fahrenheit (F) scale or the Celsius (C) scale.

Nurses should understand how to convert temperature between the scales.

The Fahrenheit thermometer is calibrated at 212 degrees. It has a freezing point of 32° F and a boiling point of 212° F. There is a 180-degree difference between freezing and boiling in the Fahrenheit scale.

The Celsius thermometer is calibrated at 100 degrees. It has a freezing point at 0° C and a boiling point at 100° C. The conversion factor used to convert between the Fahrenheit and Celsius scale is 1.8.

When comparing equivalent temperatures in Fahrenheit and Celsius, Fahrenheit will always be expressed as a larger number.

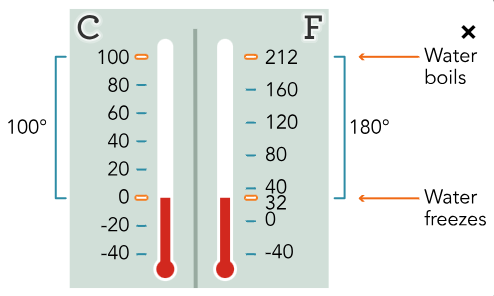
Common Temperature Comparisons

Temperature	Degrees Centigrade (° C)	Degrees Fahrenheit (° F)
Boiling point of water	100	212
Freezing point of water	0	32
Average body temperature	37	98.6

Rounding Rule for Temp:

Thermometers are calibrated to tenths. Converted temperatures should be rounded to the tenths.

Converting Fahrenheit to Celsius Steps:

Step 1: Set up the equation.

ºF  –  32 / 1.8  =  ºC​​​​​​​​​​​​​​

Step 2: Insert the Fahrenheit temperature.

97.8º F  −  32 / 1.8  =  ºC​​​​​​​

Step 3: In the numerator, subtract the client’s temperature by 32.

65.8 / 1.8  =  ºC​​​​​​​

Step 4: Divide the numerator by the denominator.

65.8 / 1.8  =  36.5555º C​​​​​​​

Step 5: Round to the nearest tenth place if necessary.

36.6º C​​​​​​​

Step 6: A temperature of 97.8° F is equivalent to 36.6° C.

Converting Celsius to Fahrenheit Steps

Step 1: Set up the equation.

(°C  ×  1.8)  +  32  =  °F

Step 2: Insert the Celsius temperature.

(39.2°  C  ×  1.8)  +  32  =  °F

​​​​​​​Step 3: Multiply the numbers within the parentheses.

(70.56)  +  32  =  °F

Step 4: Add the numbers in the equation.

70.56  +  32  =  102.56°  F

​​​​​​​Step 5: Round to the nearest tenth place if necessary.

102.6°  F

Step 6: A temperature of 39.2° C is equivalent to 102.6° F.​​​​​​​

Case Study #6: Student Nurse: I just took a client’s temperature in room 214. Their oral temperature is 38.2° C.

Nurse: The client has a medication prescribed to be administered by mouth every four hours as needed for temperatures greater than 100.4° F. Should we administer the medication?

A student nurse is caring for a client who has an oral temperature of 38.2 and has a prescription for a medication to be administered if their oral temperature is greater than 100.4° F. Which of the following actions should the student nurse recommend?

Administer the medication. The client’s temperature is 100.8° F.

The nurse should administer the medication because the client’s temperature is greater than 100.4° F. The client’s temperature is 100.8° F.

(°C × 1.8) + 32 = °F

(38.2° C × 1.8) + 32 = °F

68.76 + 32 = 100.76° F

Rounds to the nearest tenth place if necessary: 100.8° F 

A client has a temperature of 102.5° F. What is the client’s temperature in Celsius?

39.2° C

102.5° F−32​ / 1.8 =°​​​​​​​C​​​​​​​

70.5 / 1.8  =  °​​​​​​​C​​​​​​​​​​​​​​​​​​​​

39.1666  =  °C​​​​​​​

​​​​​​​Round to the nearest tenth place if necessary: 39.2° C

Time (12-hr and 24-hr)

It is important for nurses to convert between 12-hour and 24-hour time. Understanding the difference between 12-hour and 24-hour time can prevent errors.

Although most hospital facilities use 24-hour time, many clients are unfamiliar with it.

Therefore, nurses must convert between 12-hour and 24-hour time when communicating with clients.

12 Hour Clock

Time is measured using a 12-hour clock that repeats midday to account for 24 hours of the day.

The day begins at midnight (12:00 a.m.) and the second 12 hours of the day begin at noon (12:00 p.m.). This is known as 12-hour time.

In 12-hour time, hours are represented by Arabic numerals to the left of a colon, and minutes are to the right of the colon.

Medication administration errors have been made using 12-hour time if the prescriber does not mark a.m. or p.m. on the medication prescription.

• For example, if a prescriber instructs the nurse to administer a medication at 9:00, it could mean 9:00 a.m. or 9:00 p.m.

24 Hour Clock

To prevent errors, many health care facilities use 24-hour time, also known as military time.

24-hour time is based on 24 hours, not 12 hours. Because of this, each hour has a unique four-digit numerical representation.

The day begins after 0000, the first minute of the day is 0001, and the day ends at 2400.

Both 0000 and 2400 represent midnight.

When documenting 24-hour time, no colon or a.m. or p.m. is used, but four digits are always included.

The first two numbers represent hours, and the remaining two numbers represent minutes.

The first half of the day is represented in a manner comparable to both 12-hour and 24-hour time formats.

• For instance, 1:00 a.m. is 0100 hours, and 3:10 a.m. is 0310 hours. This pattern is consistent up until 12:59 p.m.

In 24-hour time, 1:00 p.m. is expressed as 1300 hours.

The hours following 1:00 p.m. are written as 1400 to 2359 hours.

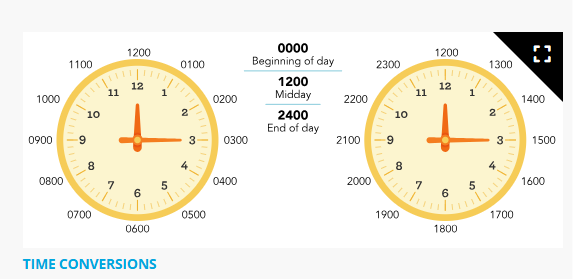
Practice Converting 12-Hour Time to 24-Hour Time

Convert 2:00 a.m. to 24-hour time.

Step 1: Remove the a.m.

2:00

Step 2: Remove the colon.

200

Step 3: Add a leading zero to have four digits if necessary.

0200

Convert 1:30 p.m. to 24-hour time:

Step 1: Remove the p.m.

1:30

Step 2: Add 12 to the hour.

1:30 + 12 = 13:30

Step 3: Remove the colon.

1330

Practice Converting 24-Hour Time to 12-Hour Time

Convert 1800 to 12-hour time.

Step 1: Subtract 12:00.

1800-1200 = 600

Step 2: Add a colon before the last two digits.

6:00

Step 3: Add p.m.

6:00 p.m.

Convert 0700 to 12-hour time:

Step 1: Remove the leading zero.

700

Step 2: Add a colon before the last two digits.

7:00

Step 3: Add a.m.

7:00 a.m

Case Study #7:

Student Nurse: Why do we have to use 24-hour time in the hospital?

Nurse: It helps reduce errors. For example, 5:00 could be interpreted as morning or evening. With 24-hour time, the hours do not repeat themselves. It is essential to be able to convert between 12-hour time and military time when educating clients.

A nurse administered a medication to a client at 0800. The client must take the medication again in 8 hours. What time should the nurse instruct the client to take the medication again?

4:00

Step 1: Add 8 hours to 0800.

1600

Step 2: Convert 1600 to 12-hour time.

Subtract 12:00.

400

Step 3: Add a colon before last two digits.

4:00

Step 4: Add p.m.

4:00 p.m.

The nurse should instruct the client to take the medication again at 4:00 p.m.

What is 12:05 a.m. in 24-hour time?

0005

In 24-hour time, midnight is 2400 and a minute after midnight is 0001. Therefore, 12:05 a.m. is 0005.

What is 2230 in 12-hour time?

10:30 pm

Step 1: Subtract 12:00.

2230-1200 = 1030

Step 2: Add a colon before the last two digits.

10:30

Step 3: Add p.m.

10:30 p.m.

Summary

In conclusion:

• When measuring volumes, nurses use metric system measurements for accuracy. Nurses commonly use the milliliter metric measurement the most. Because clients use household measurements, nurses must convert between household and metric measurements.

• Height and length are measured using metric measurements for accuracy. The most common metric measurements for height and length are the centimeter and millimeter. The most common household measurements for height and length are feet and inches. Nurses must convert between measurements to document and calculate dosages accurately.

• Many medications, especially in pediatrics and critical care, are based on clients’ weight in kilograms. Nurses must convert pounds and ounces to kilograms.  The conversion factor for kilograms to pounds is 1:2.2.

• Nurses monitor clients’ body temperatures to check for alteration in their bodies’ functioning. Temperature is monitored using the Fahrenheit (F) scale or the Celsius (C) scale. The conversion factor between the Fahrenheit and Celsius scale is 1:8.

• Time is measured within 12 hours and 24 hours. Hospitals use 24-hour time, also known as military time or the 24-hour clock, to minimize errors from occurring. Nurses must convert between 12-hour and 24-hour time, especially when communicating with clients. 

A nurse is obtaining a client's temperature. The client's temperature is 101.4° F. What is the client's temperature in Celsius? (Round the answer to the nearest tenth. Use a leading zero if it applies. Do not use a trailing zero.)

38.6° C.

A nurse is preparing to administer medication to a client at 10:00 a.m. The nurse needs to give the client the medication again in 6 hr. What time should the nurse administer the second dose using the 24-hour clock, or military time?

1600

Step 1: Add 6 hr to 10:00 a.m.

4:00 p.m.

Step 2: Remove the p.m.

4:00

Step 3: Add 12 to the hour.

4:00 + 12 = 16:00

Step 4: Remove the colon.

1600

Final answer:

The nurse will administer the second dose of the medication at 1600.

A nurse is admitting a new client to the unit who weighs 205 lb. What is the client's weight in kilograms? (Round the answer to the nearest tenth. Use a leading zero if it applies. Do not use a trailing zero.)

93.2 kg

A nurse is caring for an infant. The infant's parent reports the infant drank 6.5 oz of formula. How many milliliters of formula should the nurse document in the infant's record? (Round the answer to the nearest whole number. Use a leading zero if it applies. Do not use a trailing zero.)

195 mL

A nurse is caring for a child whose height measures 2 feet and 8 inches. How many inches should the nurse document in the child's record? (Round the answer to the nearest whole number. Use a leading zero if it applies. Do not use a trailing zero.)

32 inches

Ratio and Proportion

Step 1: What is the unit of measurement the nurse should calculate?

inches

Step 2: Set up a proportion and solve for X. Cross-multiply the numerator of the first fraction by the denominator of the second fraction. Then, cross-multiply the denominator of the first fraction by the numerator of the second fraction. Division is needed as the final step to solve the equation.

1 foot		2 feet
	=
12 inches		X inches

1X = 12 × 2

1X = 24

1X		24
	=
1		1

X = 24 inches

Step 3: Add remaining inches.

24 + 8 = 32 inches

Step 4: Determine if the measurement makes sense.

If there are 12 inches in 1 foot, it makes sense to have 32 inches in 2 feet 8 inches.

In the child's record, the nurse should document that the height of the child is 32 inches.