Geometry: Translations, dilations, symmetry, rotations, and reflections.

Translation

When the position of an object is changed

Translations Rule

Changes the position of an object

A translation is always _______.

addition

The box next to a T of translation houses what?

The coordinates you translate by

Dilation

A figure is either enlarged or reduced by a scale factor of K

If K > 1, a dilation is an ________.

enlargement

If 0 < K < 1, a dilation is a _______.

reduction

Dilations rule

Enlarges or reduces the object

A dilation is always ________.

multiplication

D2 as a dilation means

Enlargement

D1/2 as a dilation means

reduction

The k in Dk in a dilation is

what to dilate by

Line symmetry

When an object can be folded onto itself

Rotational symmetry

When the object can be rotated onto itself after less that a full term.

To find the rotational symmetry, what’s the equation?

360/n

Point symmetry

When the object can be rotated onto itself after a half turn (180 degrees)

Rotation (turn)

A figure is moved about a fixed point called a rotation center

The box right next to an R means in a rotation

the degrees you rotate by

90 degrees is a ______ turn.

1/4

180 degrees is a ______ turn.

1/2

270 degrees is a _____ turn.

3/4

Letters that are different than the original have a small roman numeral in the ____ ______ corner of them.

top right

Rotation rules

Figure is turned about a fixed point

In a rotation about the origin, the original image turns ________ (___).

counterclockwise, (CCW)

90 degrees turn (270 degrees CW) ——- Rotation

(-y, x)

180 degrees turn (180 CW) ——- Rotation

(-x, -y)

270 degrees turn (90 degrees CW) ——- Rotation

(y, -x)

Origin ——- Rotation

(-x, -y)

Reflection (flip)

Mirror image of a figure or point

Glide reflection

Consists of a line reflection and translation (combination of 2 transformations)

The box next to an r in a glide reflection is

what to reflect over

Reflection rules

Mirror image of a figure or point

Over x-axis ———Reflection

(x, -y)

Over y-axis ———Reflection

(-x, y)

Over y = x ———Reflection

(y, x)

Over origin ———Reflection

(-x, -y)

Over y = -x ———Reflection

(-y, -x)

Reflecting over a point

The point you are reflecting over becomes the midpoint

What equation do you use to reflect over a point?

The midpoint formula

What number is to the right side of the = in the midpoint formula when solving?

The rbox numbers

Composition Transformations

Combination of 2 or more transformations

In Composition Transformations, you read them _____ to ______.

right, left

Isometries/Rigid Motions

A transformation that preserves distance

All transformations are _____/____ _______ except Dilations because it changes size and distance between points.

Isometries/Rigid Motions

Direct Isometry

An isometry that preserves the order (orientation) of the vertices

Opposite Isometry

An isometry that changes the order (operation) of the vertices

Orientation for Direct Isometry

Orientation preserved

• Order the same

• Same direction as arrows

Orientation for Opposite Isometry

Orientation is NOT preserved

• Order not the same

• Different directions of arrows

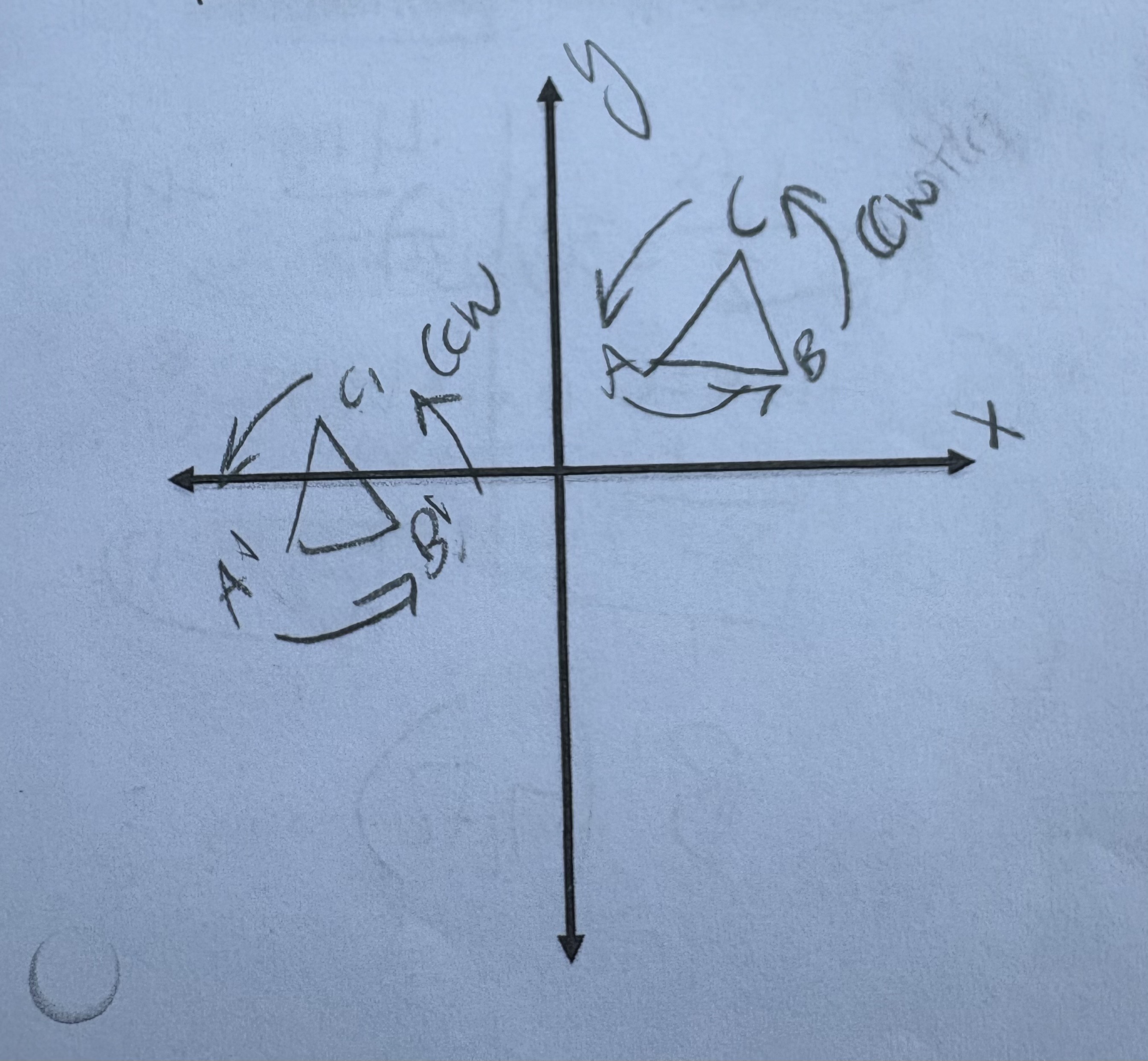
What does this image represent?

A Direct Isometry

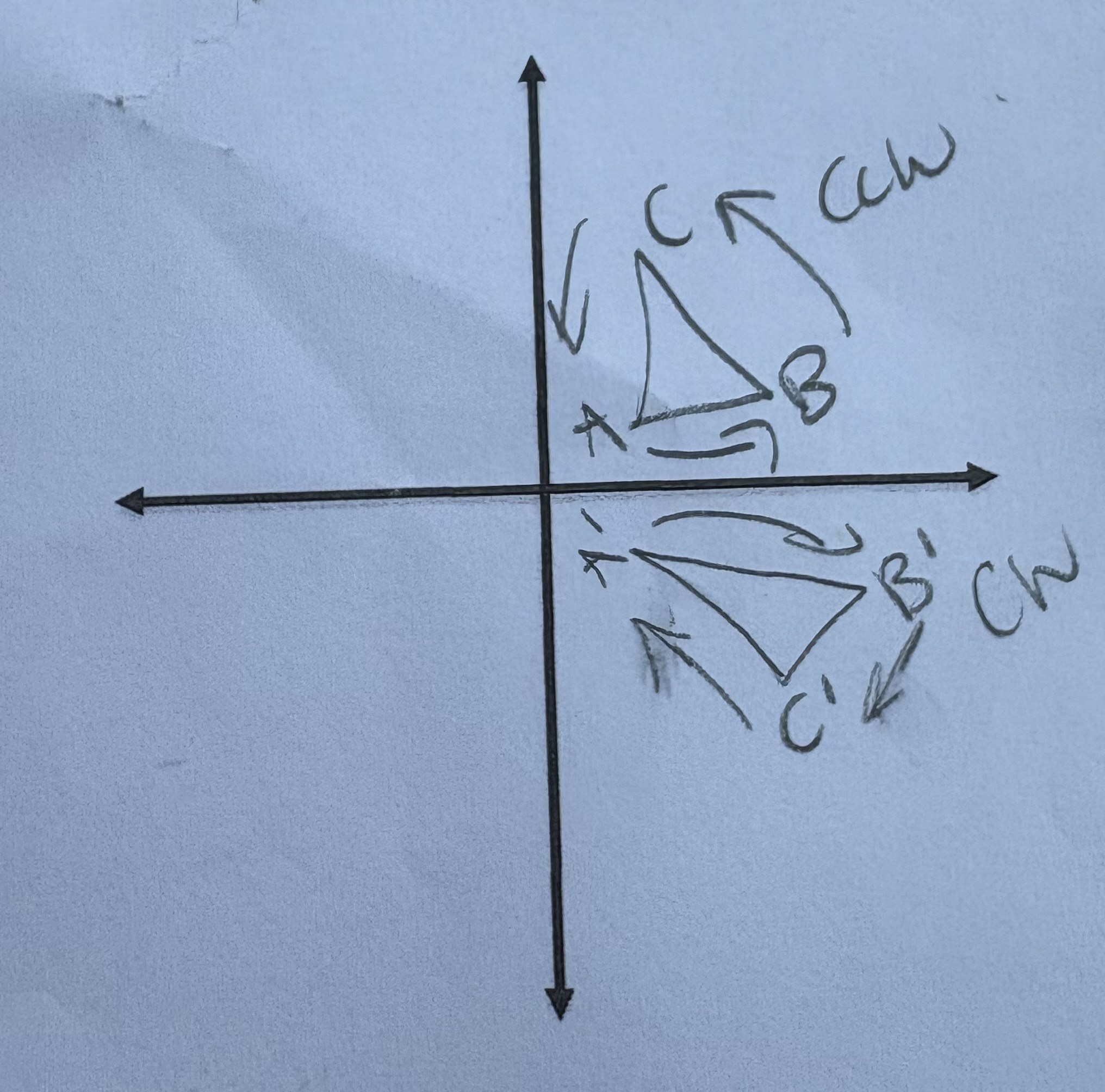
What does this image represent?

An Opposite Isometry

Isometries move figures to new location without

altering their size or shape.

Isometries _______ _______ between points.

“preserve distance”

Isometries _____ _______ between points.

“maintain congruence”

y = b is a line parallel to the __ ______ and intersects the __ _____ at b.

x-axis, y-axis

Y = b graphs a _______ _____.

horizontal line

x = a is a line parallel to the ___ _____ and intersects the __ _____ at a.

y-axis, x-axis

X = a graphs a _____ ________.

vertical line

reflect the line x = -7 over x = -2. What is the equation of the image of x = -7?

x = 3

A line that doesn’t carry a shape onto itself _____ the shape but doesn’t let the shape _____ onto itself.

flips, fold

Parallelograms have opposite ______ congruent.

sides

Parallelograms have opposite _____ parallel.

sides

Parallelograms have opposite ______ congruent.

angles

Parallelograms’ _______ bisect each other.

diagonals

Parallelograms’ consecutive angles are _______.

supplementary

A ______ divides a parallelogram into 2 ______ triangles.

diagonal, congruent

True or False: A rectangle is a parallelogram.

True

A rectangles has all angles ______.

congruent

All angles of a rectangle are ______ angles.

right

The _______ of a rectangle are congruent.

diagonals

True or False: A rhombus is a parallelogram.

True

All the _____ of a rhombus are congruent.

sides

The ______ of a rhombus bisect angles.

diagonals

The _______ of a rhombus are perpendicular to each other.

diagonals

True or False: A square is a parallelogram.

True

All ______ of a square are congruent.

angles

All angles of a square are ______ angles.

right

The ______ of a square are congruent.

diagonals

All sides of a square are ______.

congruent

The diagonals of a square _____ each other.

bisect

The diagonals of a square are __________ to each other.

perpendicular

A trapezoid has _____ pair of parallel sides.

one

An isosceles trapezoid has one pair of ______ parallel sides not ________.

opposite, congruent

An isosceles trapezoid has one pair of opposite ______ sides that aren’t _________.

congruent, parallel

The diagonals of isosceles trapezoids are _______.

congruent

The base angles of isosceles trapezoids are _______.

congruent

The opposite angles of isosceles trapezoids are _________.

supplementary