physics c magnetism equations

Magnetic Force (F_b)

qv x B (T)

Magnetic Force on Current carrying wire

I(current)l(length) x B (T)

Torque on current carrying loop of wire

N loops of wire: N i A(area) B sin(theta) theta between A and B

Biot-Savart law (dB due to current wire)

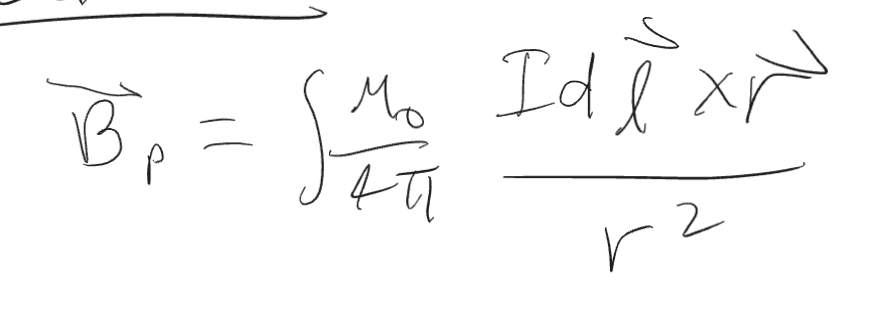
B due to a long inf straight wire

B = u_0/(2pi) (I[current]/r[dist from wire])

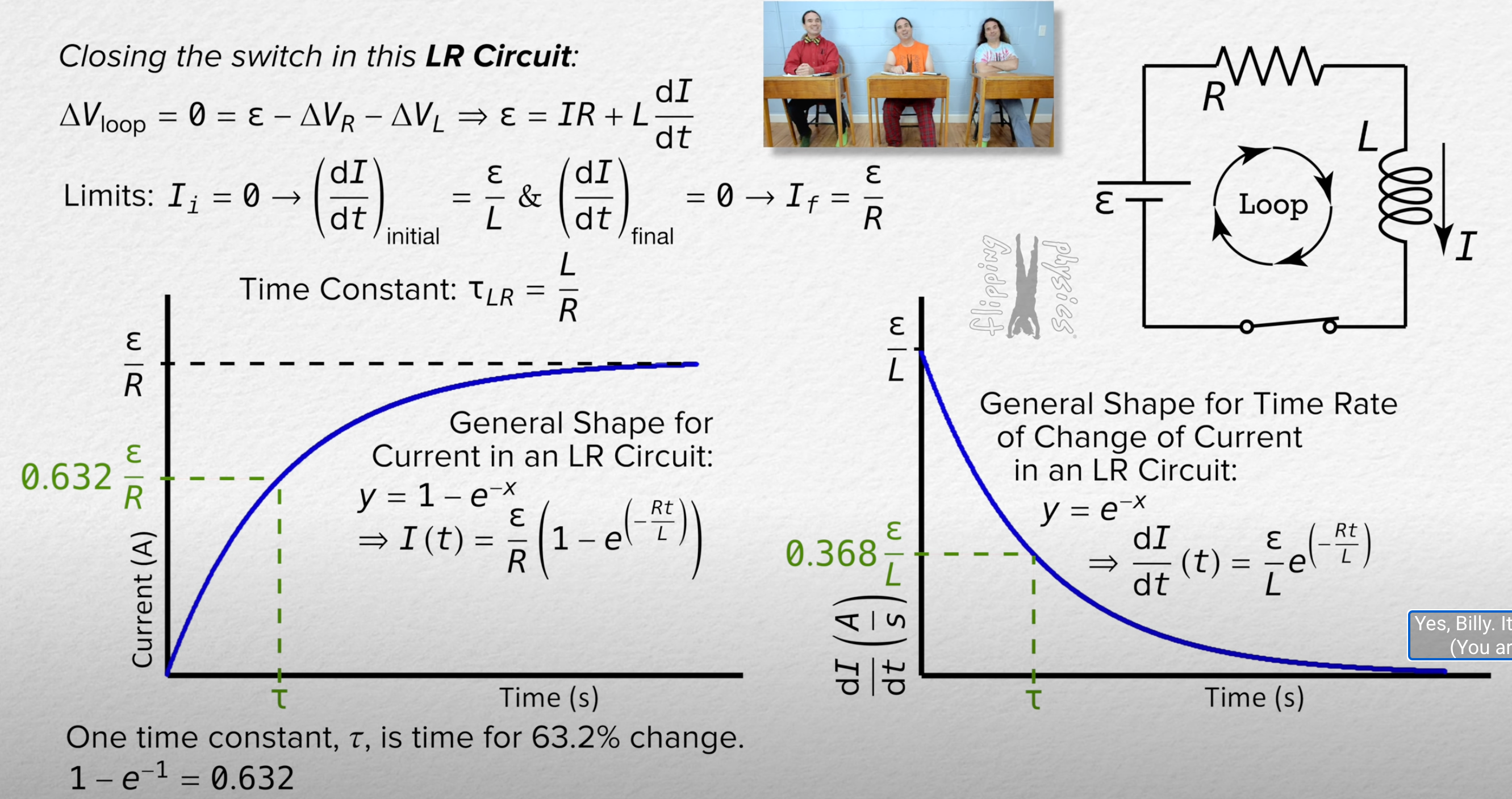
LR Circuit (init change of current & final change or current & Time constant & general shape of current)

Ampere’s Law (\int B * ds)

\int B * ds(or dl) = u_0 I_in < (current in Amperian loop)

Motional emf

emf = vBL(length of loop perpendic to velocity)

self-inductance

emf = -d(mflux)/dt = -LdI/dt ::: n = # turn per length A: cros-sec-area L = u0 n² A length

Ampere’s law + maxwell (\int B * dl)

\int B * dl = u0 I_enc + u0 eps0 d(mflux)/dt

Gauss Law (for E and B)

E: \int E dA = q_enc/esp0 B: \int B dA = 0

mutual inductance

N turns of effected solenoid N mflux/I(current)

LR circuit current

charging circuit: I = emf/R [1-e^{-tR/L}] No battery: I = I_0 e^{-tR/L}

current in a wire

I = n(charge carrier density[# charges/vol])A(crossectioonal area)v(drift velocity)q(charge per carrier)

two parallel wires force

u_0/(2pi r[dist between]) I_1 I_2

M Force of solenoid

B = u_0 n(# turns per len) I(current)