1 Meccanica razionale Capitolo 1: Geometria delle masse

quali sono le 5 proprietà della massa

1. è una grandezza scalare

2. sempre piu grande uguale a zero

3. indipendente dallo stato cinematico (dal moto del punto // sistema)

4. indipendente da trasformazioni del sistema di riferimento

5. proprietà additiva

che cosa è un punto materiale

un punto a cui viene associata una massa

come è definita la densità per un sistema continuo
quando si puo introdurre la funzione densità per un corpo continuo

la densità è definita come: Δm/ΔC per ΔC —> 0
dove ΔC è un elemento centrato in un punto P, infinitesimo di volume (ΔV) superficie (ΔS) o linea (Δl)

la funzione densità si puo introdurre sempre per un corpo continuo

quando un corpo continuo si dice omogeneo

se la funzinoe densità è una costante ed è percio uguale per ogni punto del corpo

Dimostrare che per un sistema di vettori applicati paralleli concordi e applicati nei punti Pi, con i vettori proporzionali alle masse dei punti materiali:

1. la risultante è positiva ed equivale alla massa totale del sistema per una costante di proporzionalià

2. esiste il centro del sistema di vettori

definizione di Baricentro

Si dice baricentro di un sistema di punti materiali il centro di qualunque sistema di vettori paralleli concordi proporzionali alle masse e applicati nei punti del sistema

come si calcola il baricentro per un sistema continuo

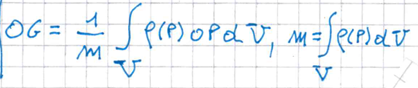
quali sono i criteri di ubicazione + dimostrazinoe:

1. se un sistema di punti materiali appartiene ad un piano allora anche il baricentro appartiene a tale piano

2. se un sistema di punti materiali è non esterno ad una superficie convessa, allora il baricentro si troverà non esternamente a tale superficie

3. se un sistema di punti materiali si trova su un segmento di retta, allora il baricentro si trova non esterno al segmento

4. il baricentro dei baricentri è baricentro

5. se un sistema ammette piano diametrale, allora il baricentro appartiene al piano diametrale

che cosa è un piano diametrale

un piano diametrale è sempre in correlazione con una retta r,

• il piano divide il sistema di punti materiali in delle coppie di punti,

• i due punti sono congiunti da segmento, parallelo alla retta r
  i due elementi di una qualunque coppia di punti hanno massa uguale e hanno il punto medio che appartiene al piano diametrale
  

Dimostrazione di criteri di ubicazione 1,2,3

Dimostrazione criteri di ubicazione 4

Dimostrazione 5° criterio di ubicazione

se un corpo ammette piano diametrale allora il baricentro si trova su di esso

come è definito il momento di inerzia

il momento di inerzia si calcola rispetto ad una retta e risulta essere per un

1. sistema discreto formato da n punti materiali di massa mi, la sommatoria del prodotto tra massa e mi e la distanza al quadrato del punto materiale dalla asse

2. per un sistema continuo si usa la densità:
   

a che cosa serve il teorema di Hygens Steiner, FORMULA!

partendo con il momento di inerzia di un corpo per un asse passante per il baricentro, con il teorema di hygensteiner si puo calcolare il momento per una qualsiasi asse parallela all’asse baricentrale.

Dimostrazione di teorema di Hygen Steiner

il momento di inerzia è un vettore?

viene influenzato da trasformazioni sul sistema di riferimento?

no è un scalare e percio non dipende da trasformazioni al sistema di riferimento

come posso legare tra di loro i momenti di inerzia di due rette parallele ma che nessuna delle due passa per il barincetro?

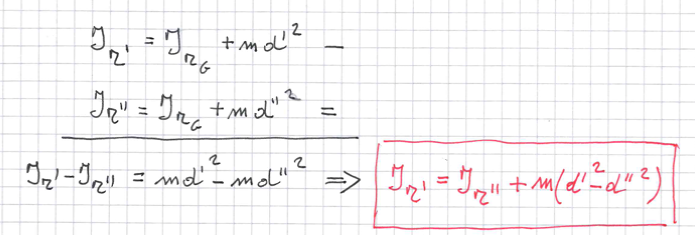
quale è la differenza tra il teorema di Huygens Steiner e la matrice di inerzia

il teorema di Huygens Steiner lega tra di loro i momenti di inerzia di rette parallele alla retta che passa per il baricentro,
la matrice di inerzia serve a calcolare il momento di inerzia di un corpo partendo da una retta passante per un punto O e in funzinoe di un versore u che determina la direzione di una nuova retta

Derivazione della matrice di inerzia

quali sono le proprietà piu importanti per la matrice di inerzia
DIMOSTRARE che la matrice di inerzia è definita positiva

• è simmetrica

• è definita positiva

formule per tutti gli elementi della matrice di inerzia

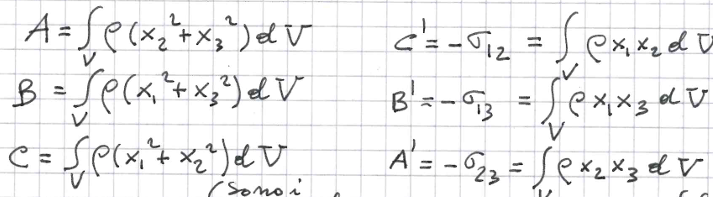
che cosa sono i coseni direttori di un versore

sono le proiezioni del versore sugli assi del sistema di riferimento,
vale che la somma dei quadrati è 1 perche un versore ha modulo unitario

quante matrici di inerzia esistono per un corpo nello spazio

dato un corpo nello spazio esistono ∞³ matrici di inerzia

che cosa sono i momenti di deviazione

sono i momenti di inerzia o gli elementi della matrice di inerzia che non stanno sulla diagonale principale

che cosa sono gli elementi sulla diagonale principale della matrice di inerzia

sono i momenti di inerzia calcolati rispetto agli assi del sistema di riferimento
percio
A —> Jx
B —> Jy
C —> Jz

quale è la definizione di asse principale di inerzia

si dice asse principale di inerzia una retta che ha come direzione la direzione di uno degli autovettore della matrice di inerzia

che cosa succede se due autovalori della matrice di inerzia sono coincidenti, che cosa succede se sono invece tutti e tre conicidenti

2. se ci sono due autovalori coincidenti allora ci sono infiniti assi principali di inerzia in quanto esiste un piano invariante per la matrice

3. se tutti e tre gli autovettori sono uguali tutto R³ è invariante

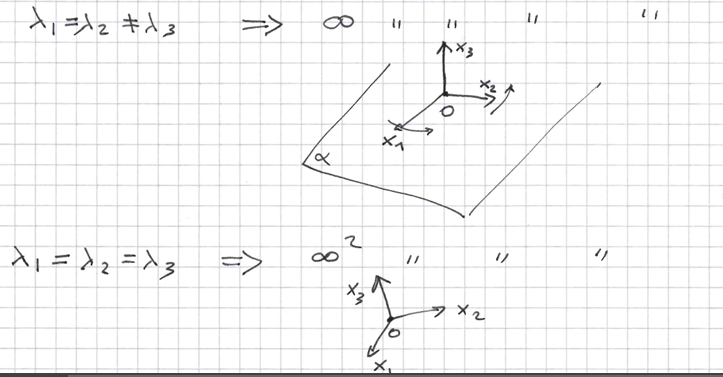
che cosa sono i momenti principali di inerzia

dato che la matrice di inerzia è simmetrica si puo diagonalizzare, in forma diagonale i momenti A, B e C si chiamano momenti principali di inerzia

che cosa è una quadrica associata ad una matrice,
quali sono i requisiti che la matrice deve avere affinché essa abbia come quadrive un ellisse

la matrice deve essere definita positiva

quale è la definizione matematica dell’ellissoide di inerzia

ellisse descritto dalla seguente forma :

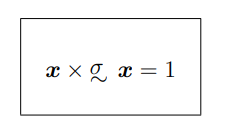
quale è la definizione Scritta dell’ellissoide di inerzia

e il luogo geometrico dei punti dello spazio la cui distanza dall’origine O, al variare della retta r di versore u è data da:

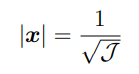
perche la quadrica associata alla matrice di inerzia è una ellisse

tra tutte le quadrice la ellisse è lunica che non ha punti impropri e percio e ben definita in ogni punto anche perche la formula accanto mostra come il valore |x| è sempre ben definitio dato che J sempre diverso da 0

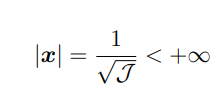
come si riesce a definire in modo grafico il momento di inerzia conoscendo ellissoide di inerzia

prima si decide la direzione dellasse in funzione di quale viene calcolato il momento di inerzia del corpo, poi si misura la distanza centro-ellissoide e con la seguente formula si calcola J
da notare che a causa del modulo di x non dipende la direzione di misurazione

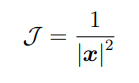
quale è a forma della quadrica associata ad una matrice di inerzia diagonalizzata

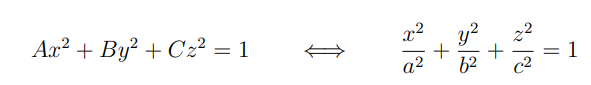
spiegare come cambia la ellissoide di inerzia se si tende al caso degenero dove tutta la massa di un corpo viene posta lungo la asse di rotazione

considerando la definizione, si nota che se uno dei momenti principali di inerzia tende a zero (A,B;C) allora x²/a² —> infinito
ne segue che l’ellisoide diventa un cilidro di inerzia

Definizione di corpo a struttura giroscopica rispetto ad un punto O

un corpo si dice a struttura giroscopica rispetto ad un punto se il suo ellissoide di inerzia rispetto al punto O è un ellissoide di rivoluzione

quando un corpo si dice giroscopio

se un corpo ha ellissoide di inerzia rispetto al baricentro di rivoluzione, simmetrico rispetto ad un asse

che cosa ci dice la forma dell’ellissoide di inerzia?
quandi autovettori uguali ha la matrice di inerzia con ellissoide di inerzia delle seguenti forme:
sfera
cilindro
ellisse simmetrico rispetto ad un asse

1. Sfera, il momento di inerzia rispetto a qualunque versore u partendo dal centro è uguale —> il corpo è una sfera
   ma matrice ha tutti e 3 gli autovettori uguali

2. cilindro, caso degenere dove tutta la massa del corpo è concentrata su un asse di rotazione,

3. ellisse di inerzia, il corpo è un giroscopio e ha 2 autovalori uguali

quanti termini della matrice di inerzia devo calcolare per un corpo che ha un asse del SdR conincidente con un API?

dato che un asse è principale di inerzia vale la regola che un autovalore è conincidente con lasse del sdR scelto:
se asse z è concorde con un autovettore di A allora vale:

e percio si annullano 2 dei tre momenti deviatori

perchè ha senso scegliere un sdR concorde con un asse principale di inerzia

perche in questo modo si annullano certi momenti deviatori e la matrice di inerzia si semplifica enormemente:

1. un autovettore concorde con un asse del sistema di riferimento
   —> due momenti di deviazione si annullano

2. due autovettori concordi con un asse del sistema di riferimento
   —> tutti e tre i momenti deviatori si annullano, essedo gli autovettori ortogonali conoscendone due ssi conoscono tutti.

Quali sono i criteri per trovare gli assi principali di inerzia, DIMOSTRARE

1. se il corpo possiede un piano di simmetria di massa, allora ogni retta ortogonale a questo piano è un asse principale d’inerzia per l’ellissoide che ha centro nel punto di intersezione della retta con il piano.

2. Se il corpo possiede due piani di simmetria fra loro ortogonali restano individuati tutti e tre gli assi principali d’inerzia di ogni ellissoide che ha il centro sulla retta di intersezione dei due piani.

3. Se un corpo possiede due piani di simmetria fra loro non ortogonali, allora il corpo ha struttura giroscopica rispetto a tutti i punti della retta di intersezione dei due piani e in particolare risulta essere un giroscopio.

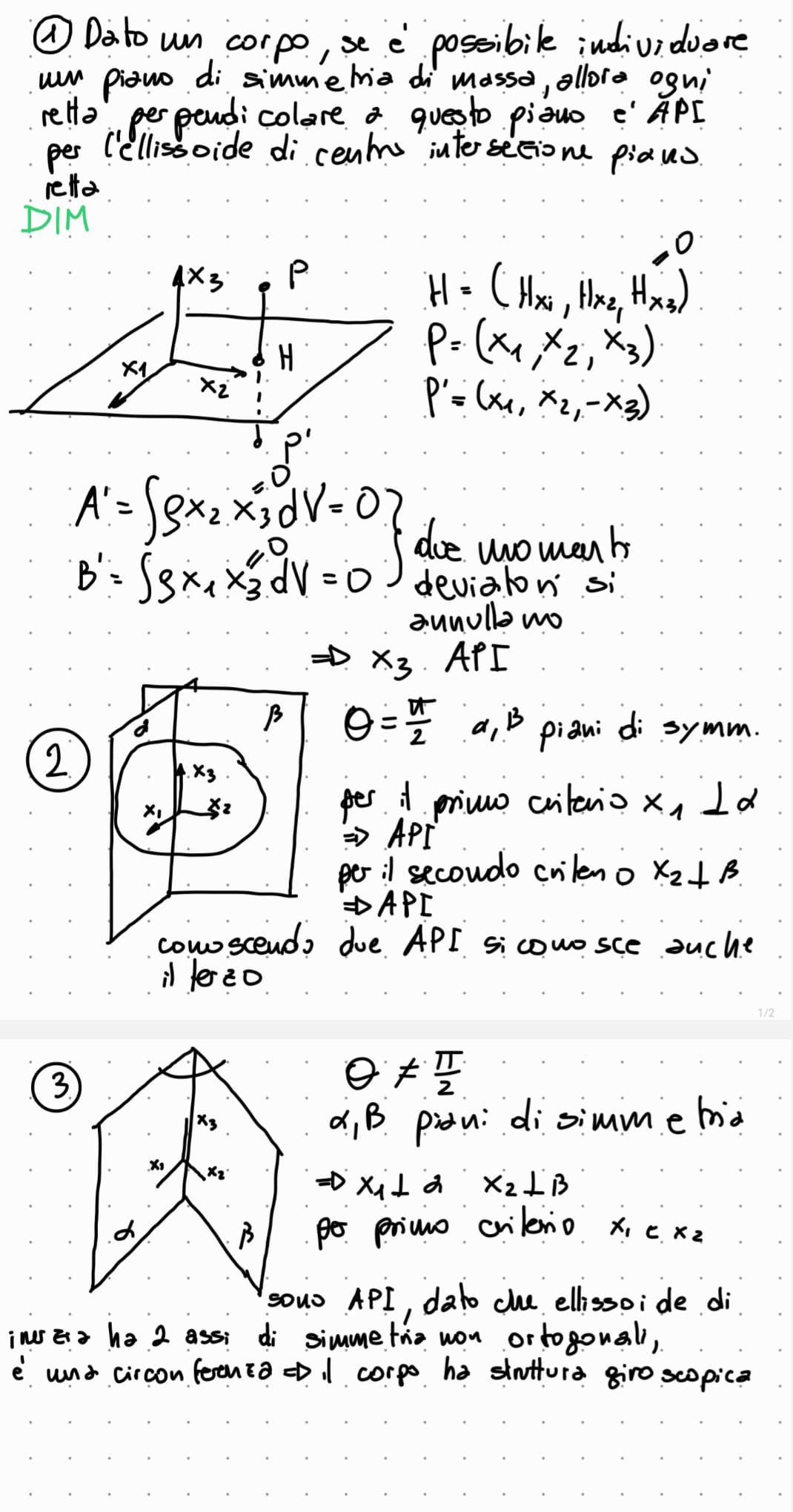
quali sono gli assi principali di inerzia per le lamine piane

ogni asse normale al piano è asse principale di inerzia per l’ellissoide di inerzia con centro nella intersezione piano-retta

come sono i momenti deviatori della matrice di inerzia per le lamine piane,
Dimostrare che ogni retta ortogonale al piano è asse principale di inerzia

dato che ogni punto ha coordinata x3 = 0 ne segue che:
A’ = integrale(rho* x₂ * x₃) = 0
B’ = integrale(rho* x₁ * x₃) = 0
da qui si puo notare che dato che si annullano 2 momenti deviatori —>x₃ è asse principale di inerzia

in piu vale che come in figura A + B = C

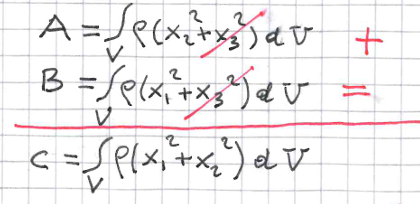
enunciare il teorema delle lamine piane

per lamine piane vale che A + B = C

enunciare il teorema di Huygens Steiner generalizzato

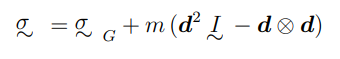
scrivere le formule che mettono in relazione i momenti principali di inerzia di una matrice di inerzia; con i momenti principali di inerzia di un sistema traslato

dove A_G sono i momenti principali di inerzia del sistema con origine nel baricentro

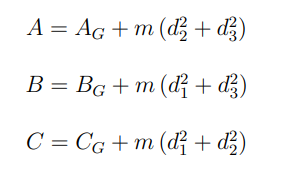
scrivere le formule che mettono in relazione i momenti di deviazione di una matrice di inerzia; con i momenti di deviazione di una matrice traslata

dove A’_G sono i momenti deviatori della matrice di inerzia calcolata rispetto al baricentro

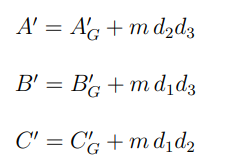
come si puo effettuare una rotazione degli assi di inerzia, come cambia la matrice di inerzia che descrive il sistema

Si usa la formula: dove R è una matrice di rotazione,

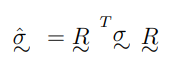
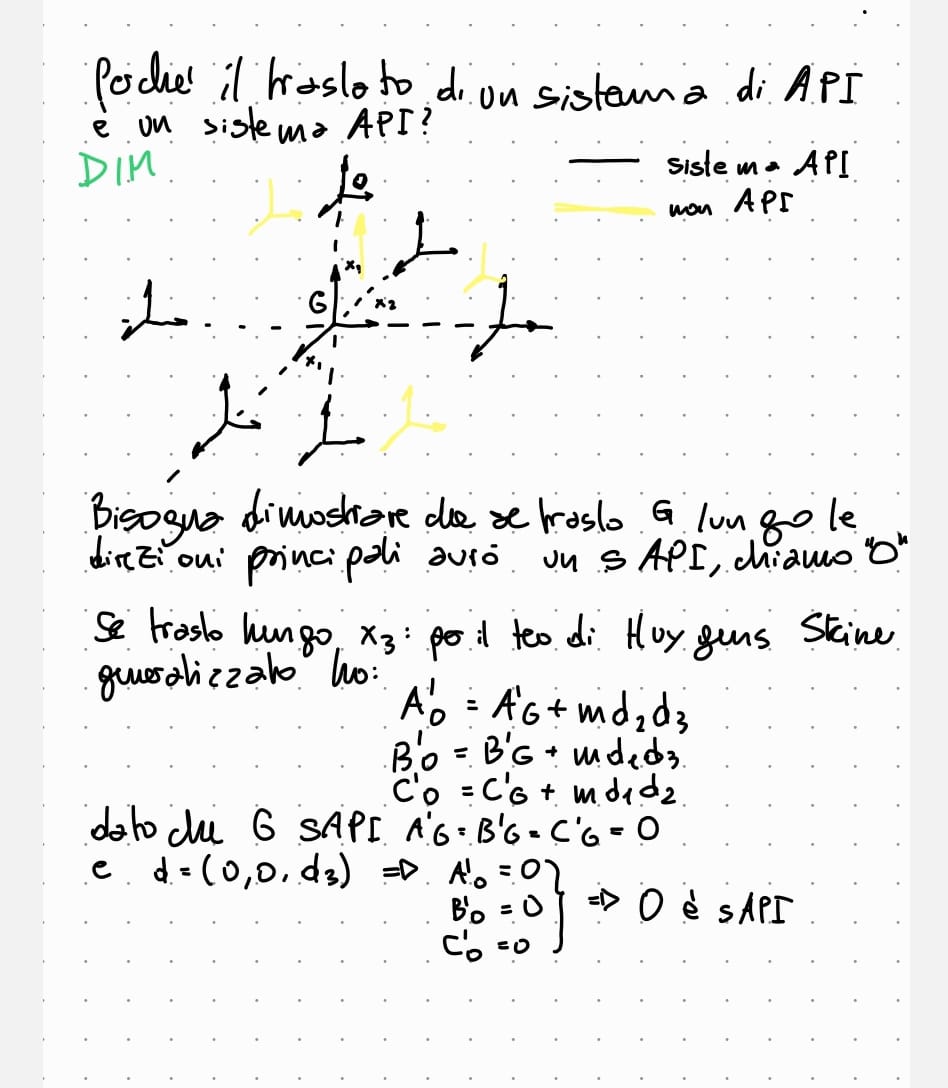
che cosa succede se ho un sistema di assi principali di inerzia e applico una traslazione lungo la direzione di uno degli assi?
DIMOSTRARE

il sistema traslato ottenuto è formato da 3 assi principali di inerzia

che cosa succede se traslo un sistema di API lungo una direzione che non coincide con le direzioni individuate dal sistema di API?
NOTA: dato che si parla solo di traslazioni e non di rotazioni, la direzione di spotamento sarà per forza parallela ad uno dei 3 API

se applico una traslazione parallela ad un API ma non concorde con la retta di azione, allora: il sistema in generale non è un sistema formato da API
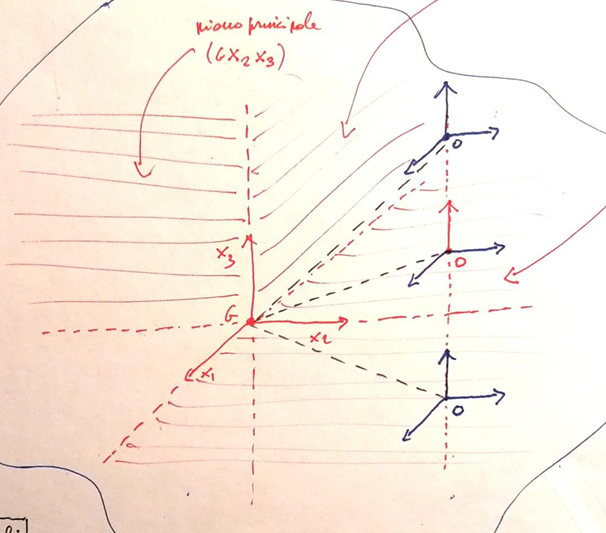
MA: quando il sistema traslato è coincidente con un piano normale alla direzione di traslazione e coincidente con il sistema di API iniziale, allora la asse ortogonale al piano è API

Nel disego, in blu sono gli assi non API, in rosso invece sono API. si nota che quando il sistema traslato è conincidente con il piano individuato da x1,x2. allora l’asse parallelo a x3 è API

come si comporta la matrice di una lamina piana se applico una rotazione attorno ad un asse ortogonale al piano della lamina?

dallimmagine si nota che se se A = B (corpo a struttura giroscopica) allora A’ = B’
e C’ = 0,
ne segue che a seguito di rotazioni attorno allasse ortogonale, lasse ortogonale del sistema ruotato è API e se il corpo è a struttura giroscopica allora questa rotazione non cambia la matrice di inerzia

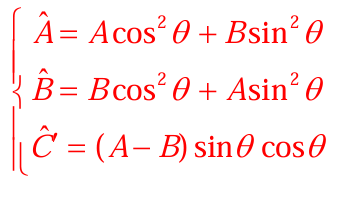
che cosa è il raggio di girazione

considerando il momento di inerzia J di un corpo di massa m lungo un asse r
il raggio di girazione è:
notare che è il raggio tale per cui se metto la massa dellintero corpo in un punto lo devo spostare ad una distanza r dallasse di rotazione per avere lo stesso momento di inerzia del corpo inizialemente

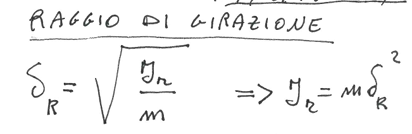
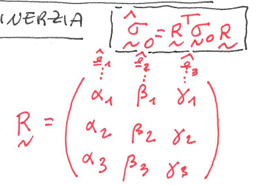
come ruotare una matrice di qualunque angolo:

dove alpha beta e gamma sono i coseni direttori del sitema ortonormale di vettori ruotati

che cosa succede se traslo un sistema di assi principale di inerzia per un vettore che ha una componenete nulla (il sistema traslato sta su uno dei piani generati dai due dei tre assi del sistema di assi principali di inerzia)
DIMOSTRARE

l’asse ortogonale al piano è asse principale di inerzia