5-Energy, 6-Materials

forumla for work done

work done = force x distance moved in direction of force

what is another way of saying work done

energy transferred

how to derive kinetic energy formula

v^2 = u^2 + 2as

when u= 0, s= v^2/2a

w=fx, subbing in x for s --> w=f(v^2/2a)

as f=ma, w=mav^2/2a

cancelling the a's --> w=1/2mv^2

derivation for gravitational potential energy equation

w=fx

f=ma, where a = g, and x = distance from ground=height

therefore w=mgh

define power

rate of energy transfer

derive another power equation using work done formula

p=w/t

w=fx so p=fx/t

so p=fv

what is hooke's law

For a material within its elastic limit, the force applied is directly proportional to the extension of the material

what is the force constant k representing

a measure of stiffness

what is elastic deformation

The concept that a material WILL return to its original shape when the force is removed.

what is plastic deformation

The concept that a material will NOT return to its original shape when the force is removed.

derive elastic potential energy formula using area under graph of force-extentsion

-area = 1/2 base x height

-base = x, height = f

-E = 1/2fx

-f=kx

-E=kx^2

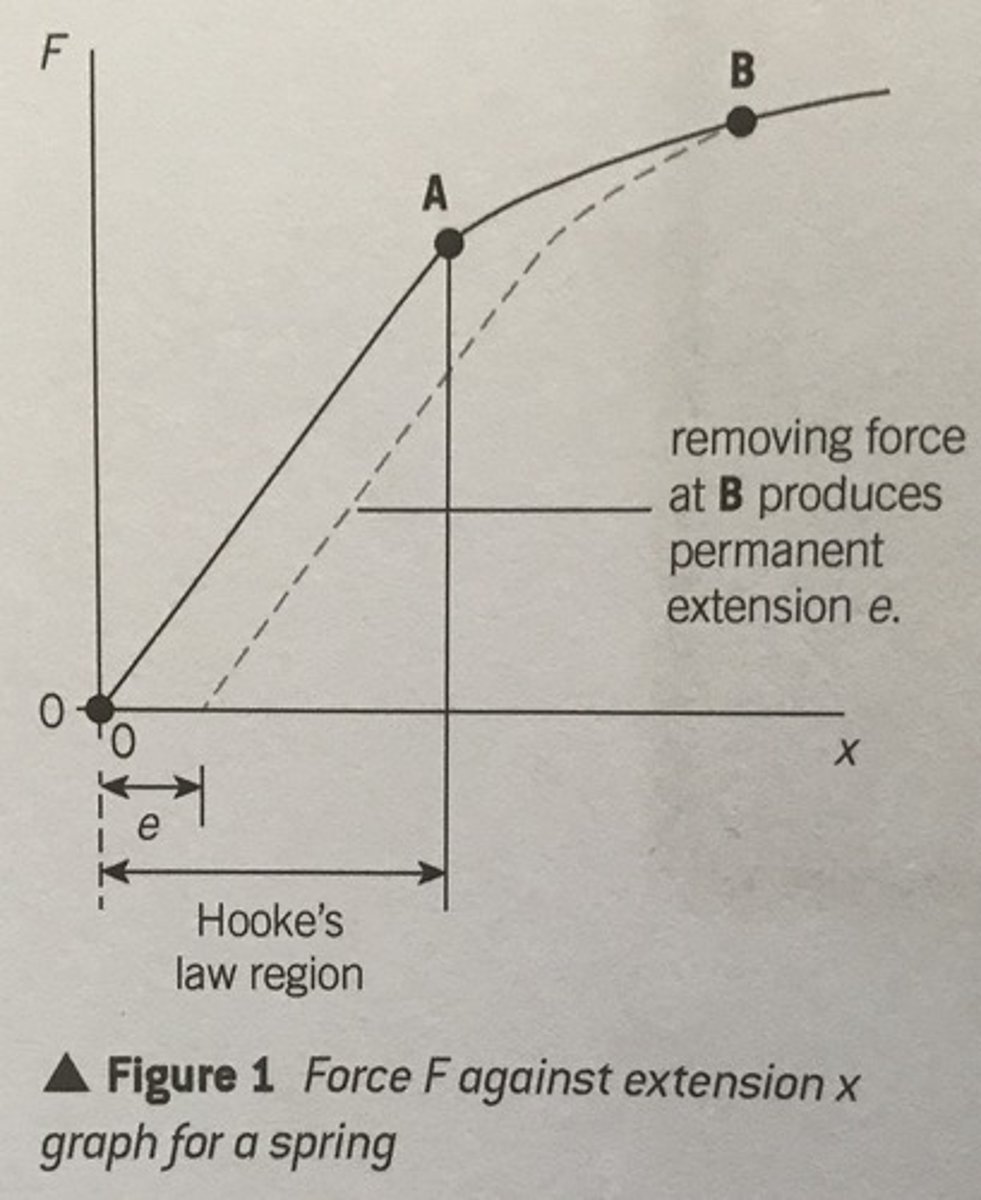
force-extension graph for a spring + explain where elastic & plastic region is and hooke's law regions

- until point A, Hooke's law is obeyed + elastic region

- After point A, Hooke's law not obeyed + plastic region ∴ permenant extension

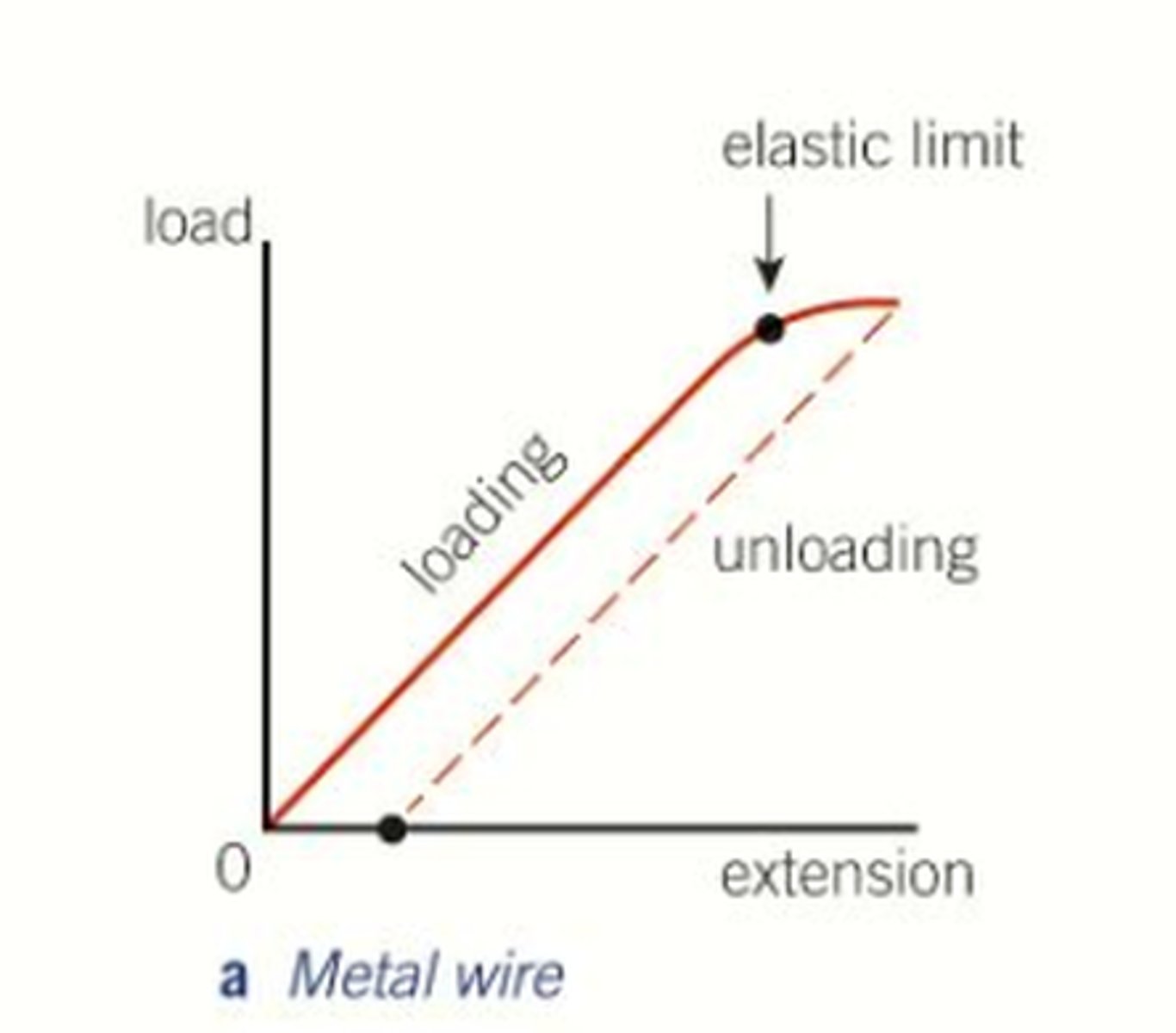
force-extension graph for a wire + explain where elastic & plastic & hooke's law region is

- until elastic limit = elastic deformation + Hooke's law

- after elastic limit = plastic deformation + permenant extension

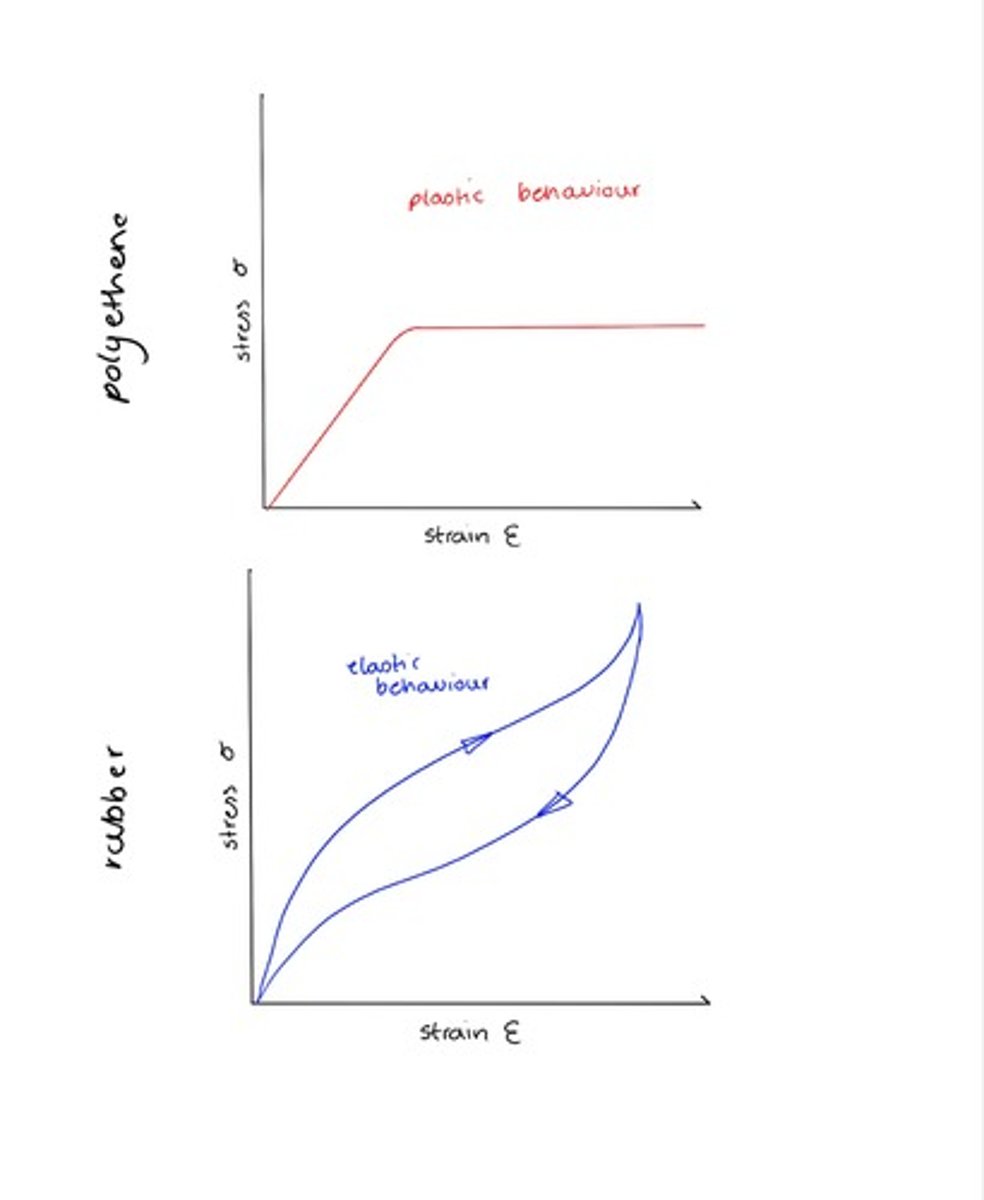
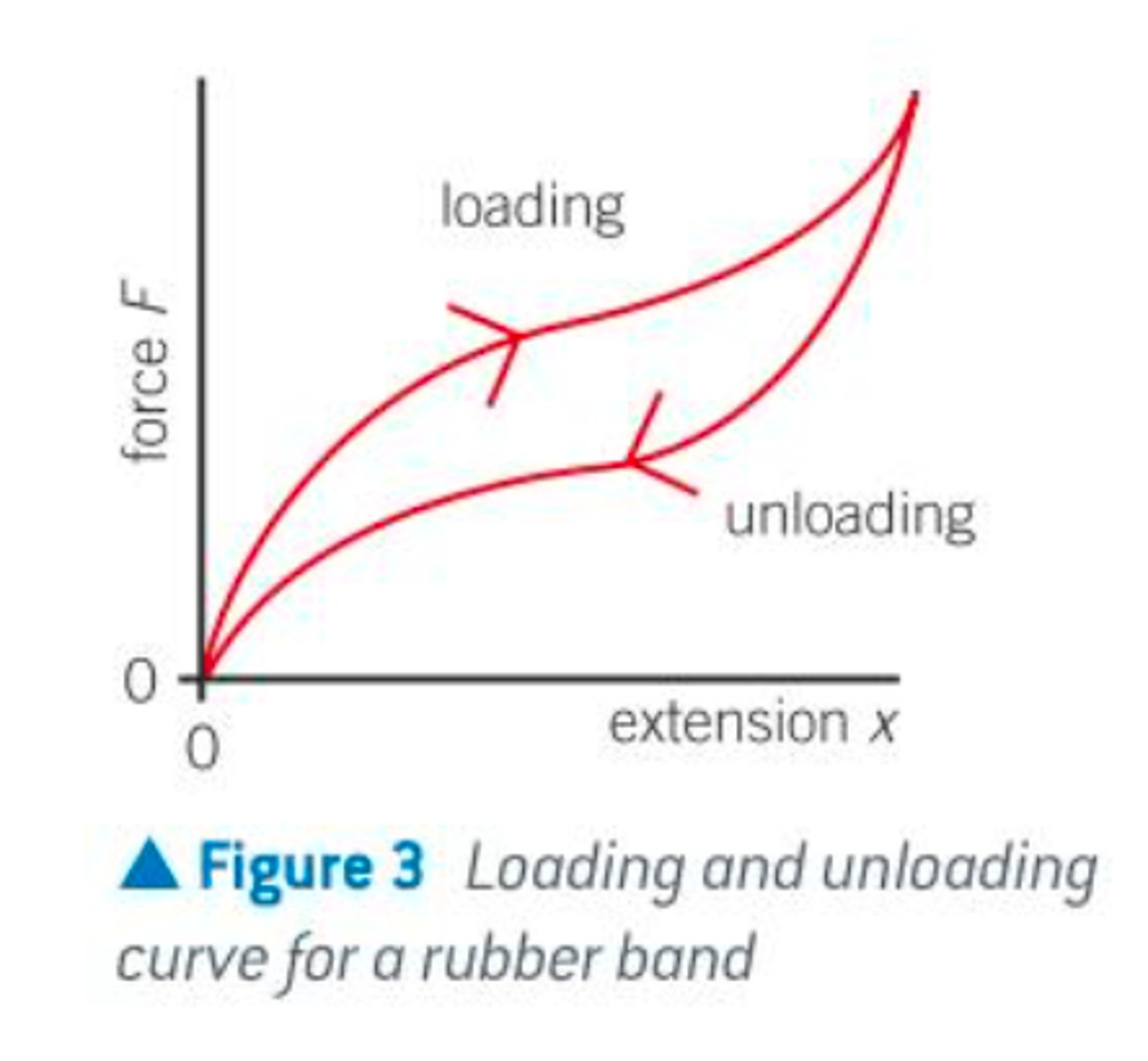
force extension graph for rubber + explain elastic plastic & hook'es law regions + energy

- does not obey Hooke's law

- undergoes elastic deformation, not plastic deformation

- the area between the loading and unloading curve is a hysteresis loop - the area = energy required to stretch the material out which was then transferred to thermal energy when the force was removed ∴ representing the energy loss

force-extension graph for polyethene + explain plastic elastic hooke's law regions + what is a good use?

- polymeric material does not obey Hooke's law

-experiences only plastic deformation when any force is applied to it

- easy to stretch into new shapes

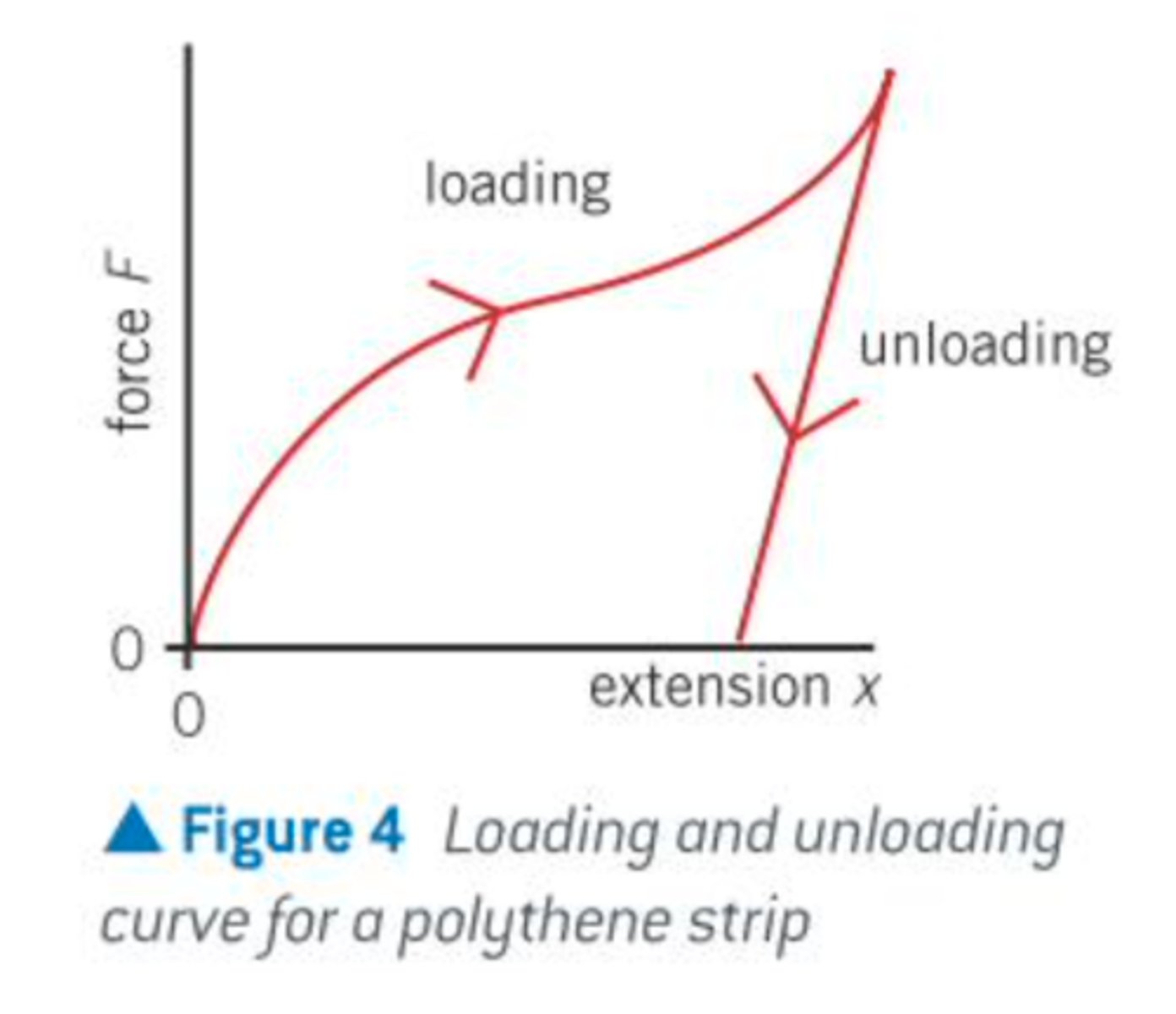
Define brittle

- Undergoes little/no plastic deformation before breaking

- Cracks/shatters suddenly (soon after the elastic limit is reached)

Define ductile

- can undergo significant plastic deformation before breaking

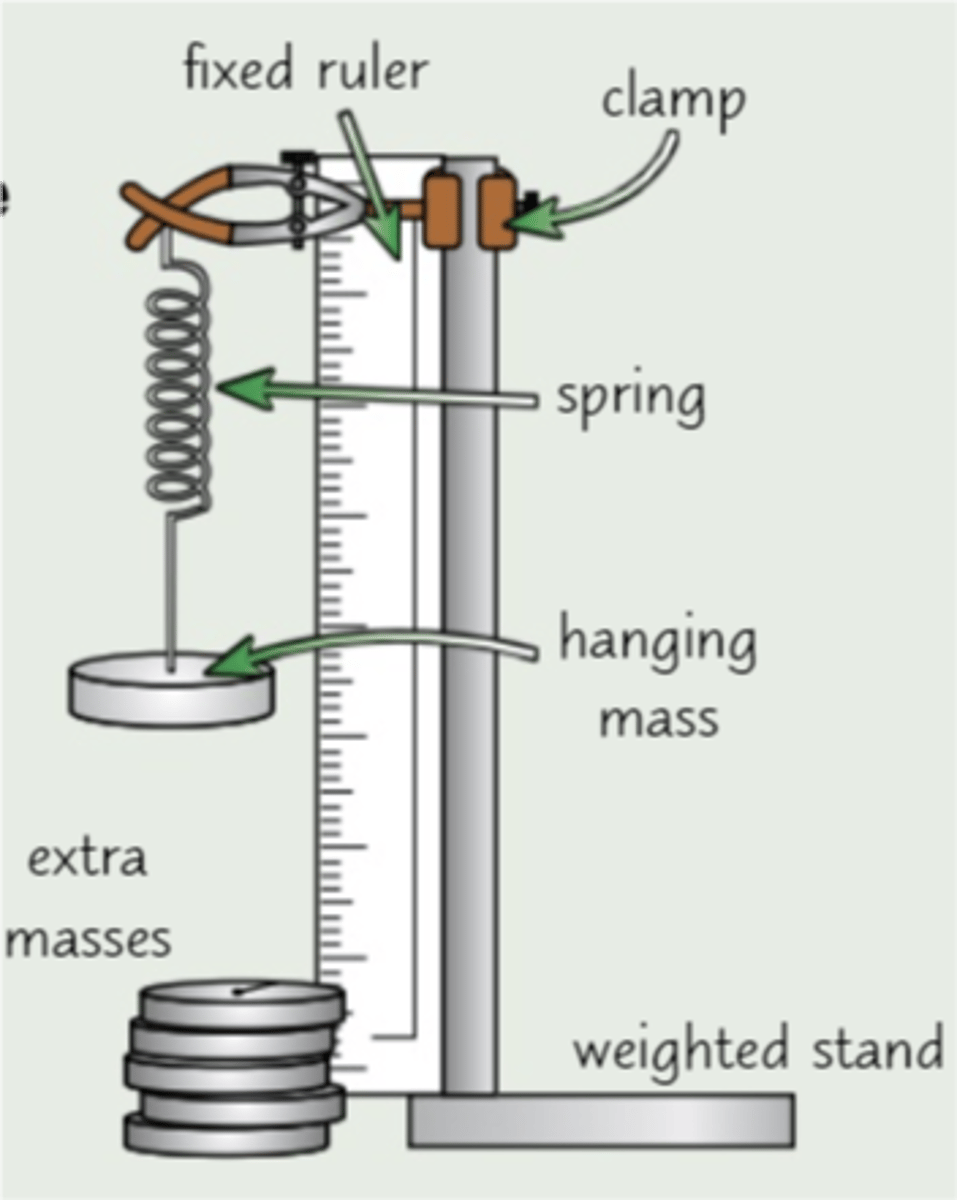
force and extension experiment (method)

1. Set up the equipment as shown

2. Record the length of the spring with no force attached

3. Hang a 1N weight on the end of the spring

4. Record the new length of the spring

5. Continue adding more weight and recording it until you have enough results

6. Subtract the unstretched length from each reading, this is the extension

7. Plot a force-extension graph - gradient should be the force constant

evaluating the force-extension experiment; how to reduce systematic errors ?

- reduce parallax error by reading the metre at eye-level

-use a fiducial marker to mark the orginial position of the material

evaluating the force-extension experiment; how to reduce random errors ?

- ensure material is stationary before a reading is made

- repeat the experiment several times and calculate an average

evaluating the force-extension experiment; safety precautions ?

- eye protection worn

- landing mat placed below the clamp stand to catch the weight if it falls

- do not stand directly underneath the hanging masses

define tensile stress + define ultimate tensile stress

- The force per unit cross-sectional area, measured in Pa

- UTS = the maximum force per original cross-sectional area a wire is abl eto support unitl it breaks

explain what the Young's Modulus is

- the ratio of stress to strain (Pa)

- represents a material's ability to resist deformation under stress (stiffness)

difference between force constant & Young's Modulus

- force constant is specific to object's shape and size

- Young's Modulus is an intrinsic property of a material

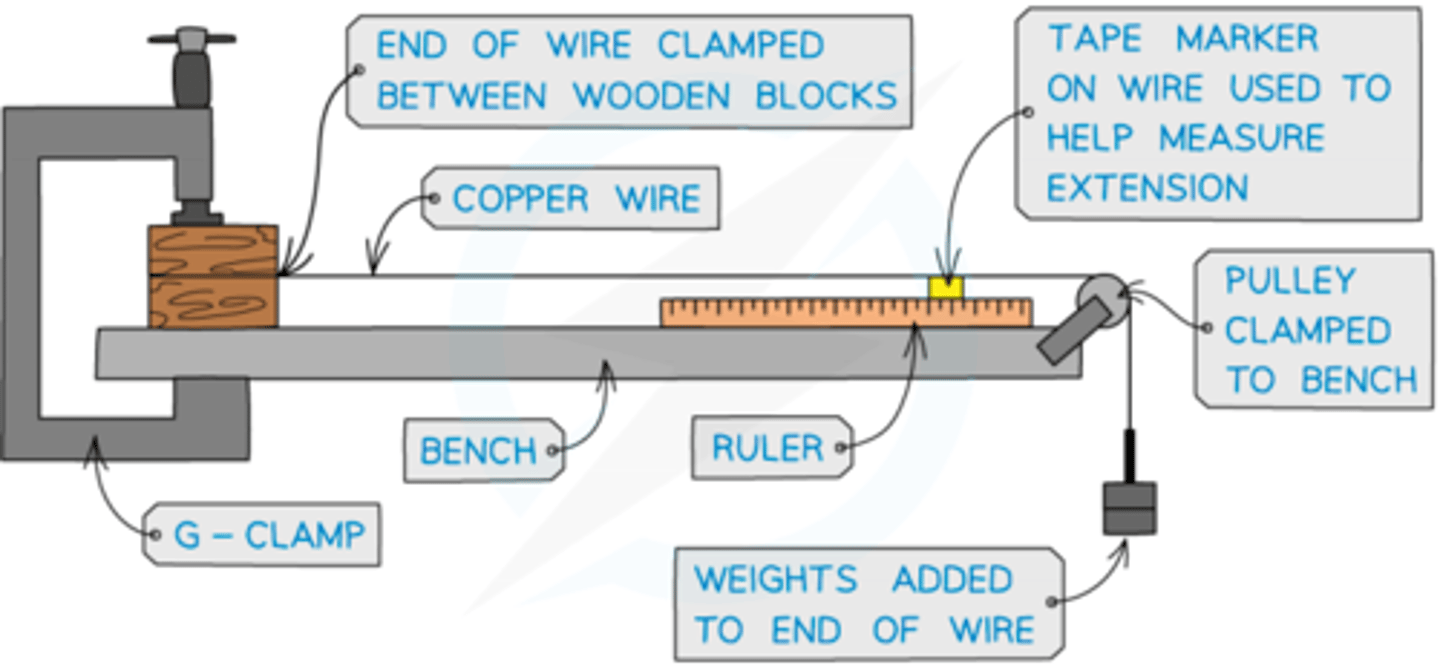
Young modulus experiment

- setup experiment as shown

- measure diameter of the wire with a micrometre taking 3 measurements at different points and calculating an average

-measure the original length and mark a reference point with tape

- add 100g mass onto the mass hanger

- read and record the new reading of the tape marker from the ruler

- repeat this by adding another mass and record the new readings

- calculate stress and strain and plot graph

- gradient is young modulus

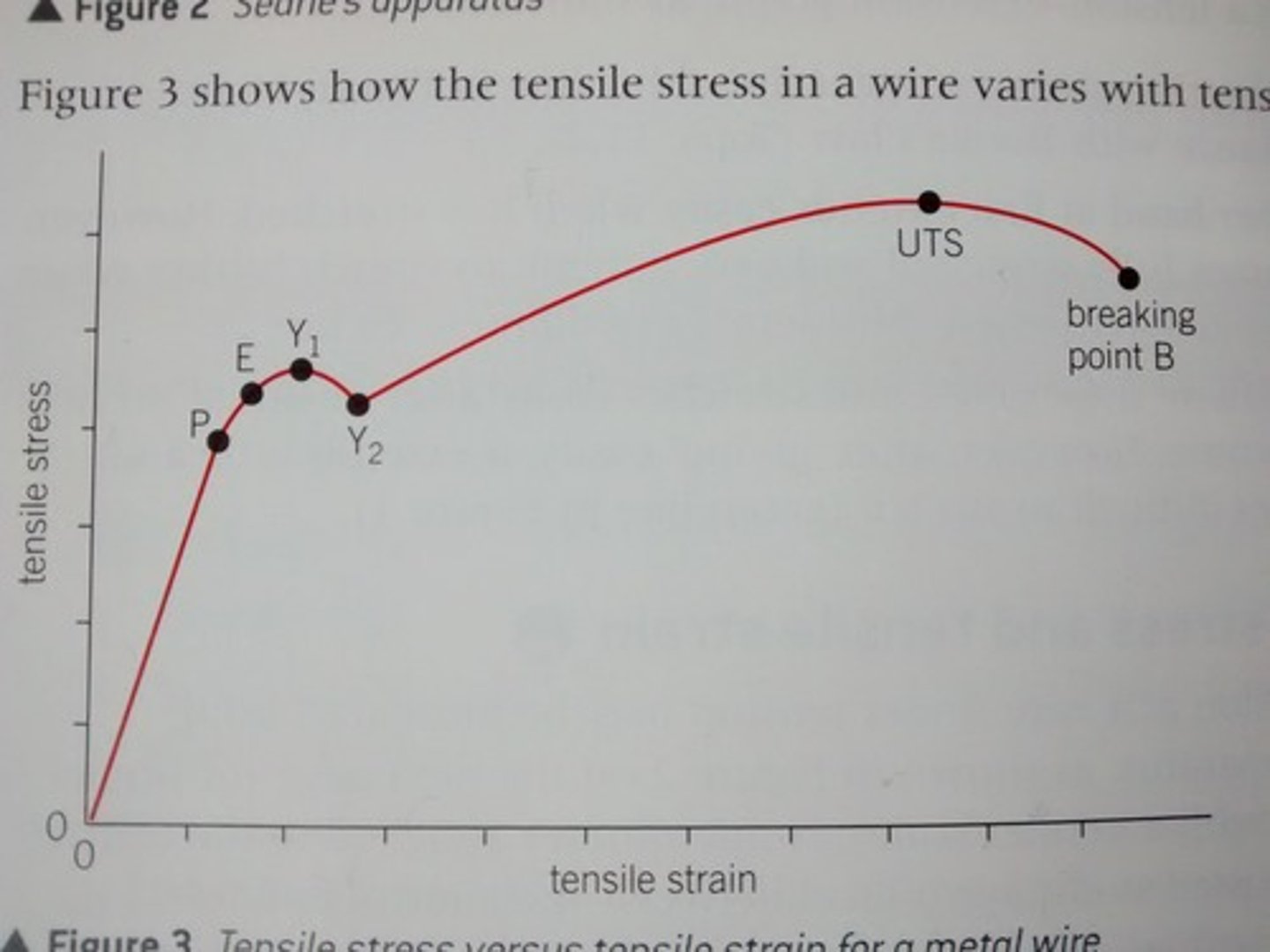
The stress strain graph for a ductile material?

what do each point represent?

P = limit of proportionality

E = elastic limit

Y1 & Y2 = upper and lower yeild points

UTS = ultimate tensile strength

B = breaking point

stress-strain graph for a brittle material

- Elastic deformation until the breakpoint (no plastic)

- Loading and unloading curve identical

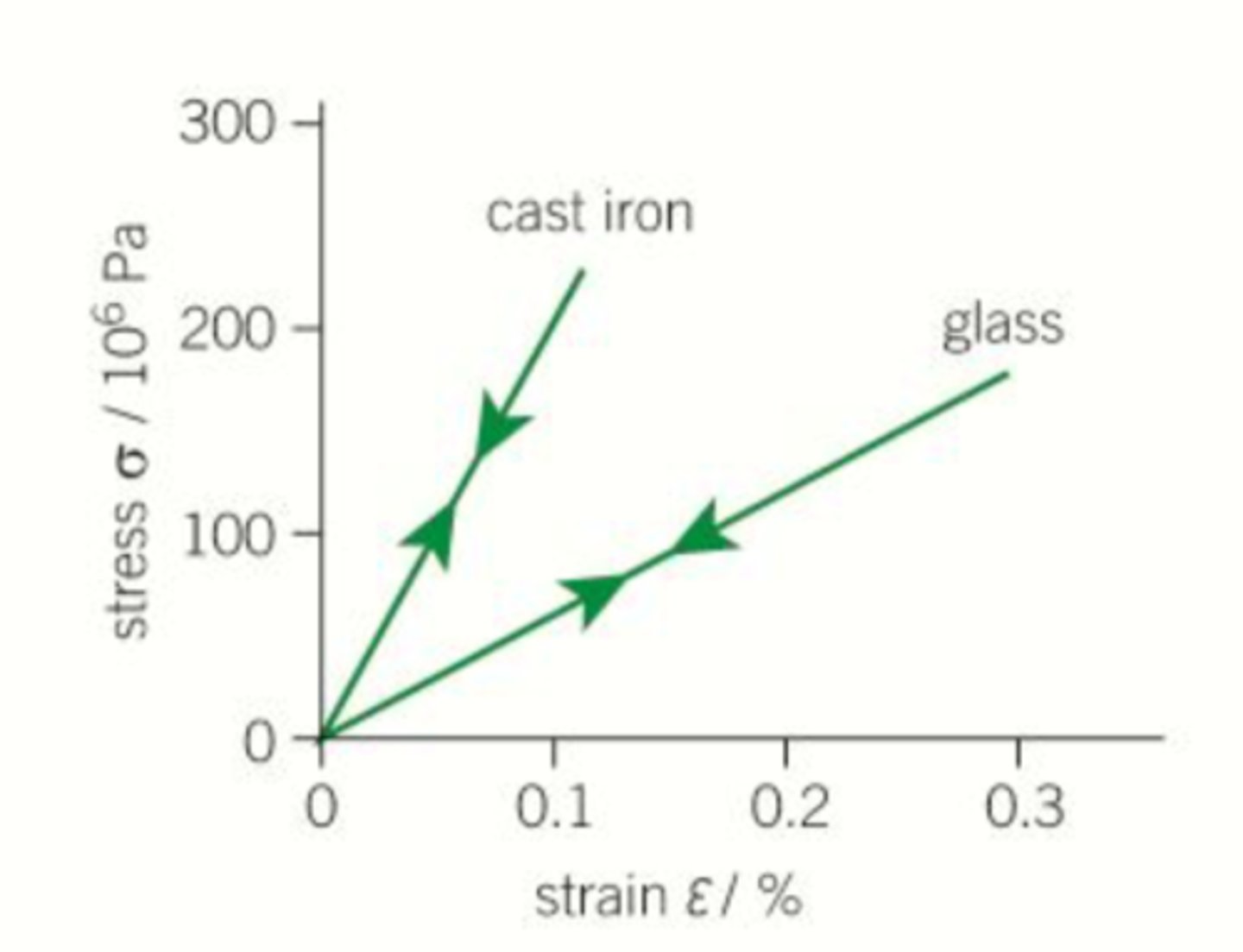
stress-strain graph for polymeric materials

- rubber shows elastic behaviour

- polyethene shows plastic behaviour