2 - functions + graphs

ways of saying input

domain

object

x

ways of saying output

range

image

y

one-to-one function

one input = one output

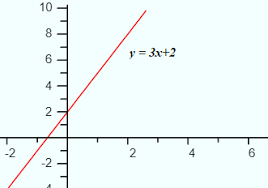
many-to-one function

many inputs = one output

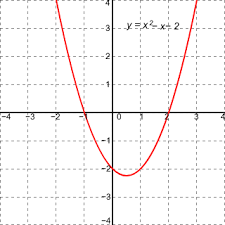
one-to-many function

one input = many outputs

nb: this is not a function because you can’t find the inverse

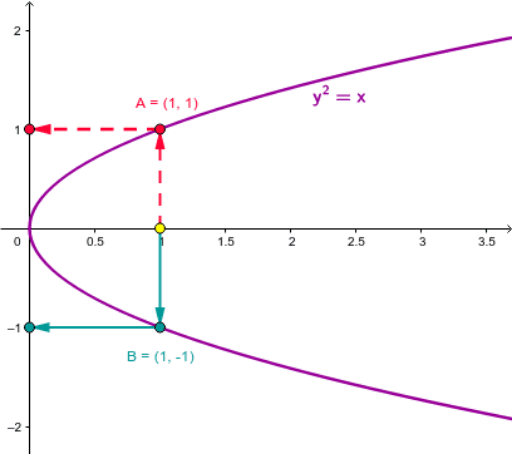
how can you turn a one to many into an actual function

restrict the domain:

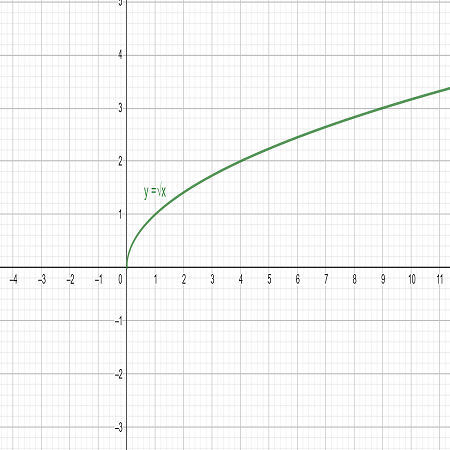
y² = x —> y = √x —> y = √x when x≥0

many-to-many function

many inputs = many outputs

when is knowing all these types of function useful

‘find the range’ or ‘find the domain’ questions

always draw it out to visualise and answer these

what does ℤ mean

integer - whole number

what does ℤ⁺ mean

positive integer - whole number greater than 0

what does ℕ mean

natural numbers - whole number greater than or equal to 0

what does ℚ mean

rational numbers - can be written as a fraction

what does ℝ mean

real numbers - every number that’s not imaginary

how can you visually describe an inverse function

reflection in the line y = x

how can you use an inverse function to solve for x (the point where it meets its original function)

these three lines intersect:
- normal function
- inverse function
- y=x

so you can set them equal to one another to find x (the point where they meet)

what is the modulus of something

its absolute value (always positive)

|x|

if a function is positive, what’s its modulus |f(x)|

the same as the function

if a function is negative, what’s its modulus |f(x)|

-f(x)

reflect any negative parts in the x-axis (so the range is all above zero)

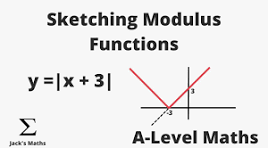
how do you draw a graph f(|x|)

draw the graph for x≥0

reflect the graph in the y-axis

when solving where a modulus and regular function intersect, what two things must work with your answers

visual intersection

algebraically being equal

to solve modulus problems algebraically what’s one thing you have to make sure

the modulus bit is alone on it’s side of the equation