Estadística Descriptiva - Unidad 3: Medidas estadísticas

Conoce las medidas estadísticas que nos enseñan las diferentes características de las distribuciones de datos.

Medidas estadísticas

Medidas estadísticas

Valores que definen las características de las variables cuantitativas.

Medidas estadísticas

Resumen la información de los datos, nos permiten analizar la dispersión y tendencia central del conjunto, nos otorgan valores representativos que permiten compararlos con otros conjuntos respecto a diferentes características y son de fácil interpretación.

Medidas de frecuencia

Son herramientas utilizadas para describir la distribución de los datos en un conjunto de observaciones, como lo es su incidencia o repetición.

Moda

Valor que ocurre con mayor frecuencia en un conjunto de datos. Es una medida de tendencia central que se utiliza para describir la forma de la distribución de los datos.

Unimodal

El conjunto de datos sólo tiene una moda.

Bidomal

El conjunto de datos tiene dos modas.

Multimodal

El conjunto de datos tiene más de dos modas.

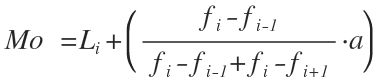
Se toma el conjunto con mayor frecuencia absoluta y se procede a coger su límite inferior + (la frecuencia absoluta - la frecuencia absoluta anterior)/(frecuencia absoluta - frecuencia absoluta anterior)+ (frecuencia absoluta - frecuencia absoluta siguiente)

Fórmula para la moda para datos agrupados en intervalos

Medidas de posición

Son indicadores estadísticos que permiten resumir los datos en uno solo, o dividir su distribución en intervalos del mismo tamaño. No nos proporcionan información confiable sobre la distribución y son sensibles a los valores extremos, sin embargo no dependen de la escala y son fáciles de interpretar.

Mediana

Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor. Es una medida de tendencia central.

n/2

Cómo calcular la posición de la mediana

Cuartil

Divide la distribución en cuatro partes iguales.

3

Cuántos cuartiles hay?

Cuartil 1 (Q1)

Es mayor al 25% de los datos.

Cuartil 2(Q2)

Es mayor al 50% de los datos. También es conocido como la mediana y coincide con el quinto decil.

Cuartil 3 (Q3)

Es mayor al 75% de los datos.

Quintil

Es un cuantil que divide una distribución de datos ordenados en cinco partes iguales. Es menos frecuente que el cuartil

Decil

Son los nueve valores que dividen a un conjunto de datos ordenados en diez partes iguales.

Percentil

Son los valores que dividen a un conjunto de datos ordenados en cien partes iguales.

nK/t

Cómo calcular la posición de las medidas de posición?

Ubicación de un percentil

(n + 1) (P/100)

Cuantil que estemos calculando. Ej: decil = 10, cuartil = 4, etc.

Qué es T?

Cogemos el límite superior de esta frecuencia acumulada, y esa será nuestra mediana.

Qué pasa si al calcular la posición de la mediana encontramos el número en una de las frecuencias absolutas acumuladas?

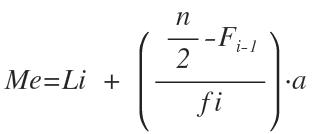
Tomamos la frecuencia acumulada directamente psoterior a la posición de la mediana y luego: *Límite inferior + (n/2 - frecuencia acumulada anterior)/(frecuencia absoluta)i

Fórmula de la mediana para datos agrupados.

Límite superior - Límite inferior + 1

Cómo calcular i?

Cogemos el la frecuencia acumulada posterior a la posición del cuantil que estemos calculando, y luego: Límite inferior + i(nk/t -frecuencia acumulada anterior)/frecuencia acumulada - frecuencia acumulada anterior)

Fórmula para calcular los demás cuantiles

Medidas de representación

Son herramientas que se utilizan para resumir y describir un conjunto de datos.

Media aritmética

Es un valor central característico de un conjunto de datos estadísticos. Es uno de los principales indicadores que se utilizan para hacer un estudio estadístico de una muestra. Es una medida de tendencia central que se utiliza para describir un conjunto de datos.

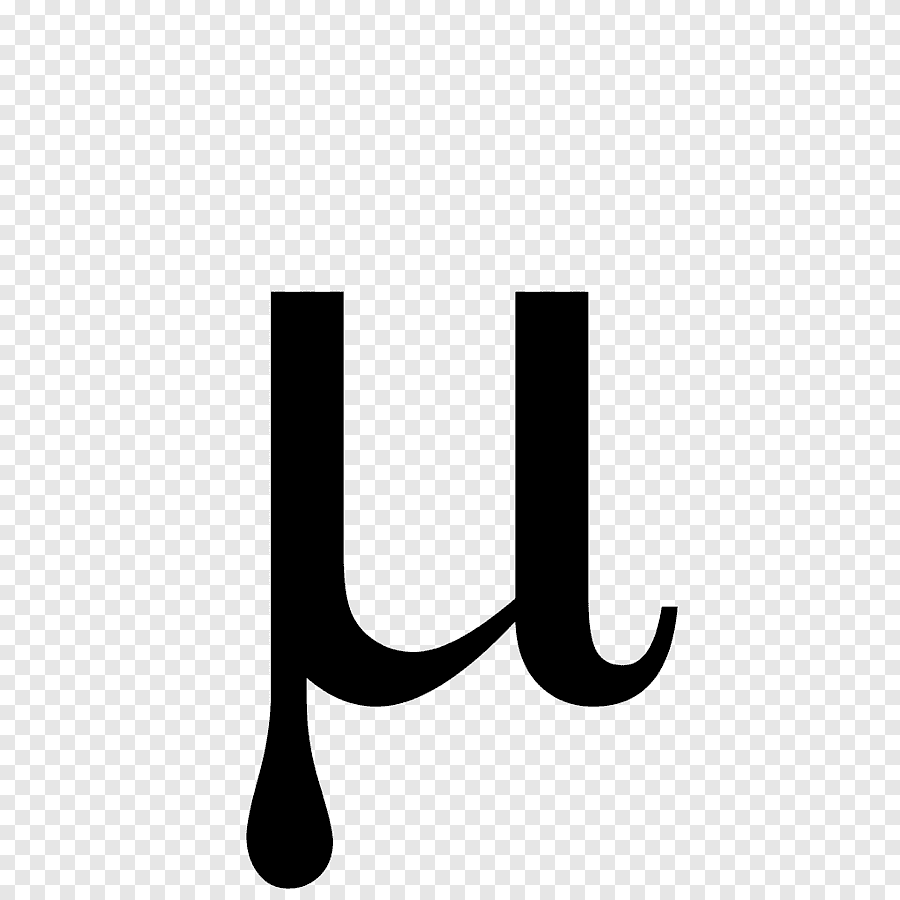
Símbolo de la media aritmética poblacional

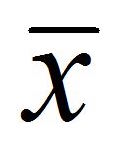
Símbolo de la media aritmética muestral

Media geométrica

Se le calcula la raíz, con coeficiente de n/N, al producto de un conjunto de números estrictamente positivos. Se utiliza comúnmente para calcular el promedio de datos que siguen una distribución logarítmica, como las tasas de crecimiento o los precios de las acciones.

Fórmula de la media geométrica

Media armónica

Es igual al número de elementos de un grupo de cifras entre la suma de los inversos de cada una de estas cifras. Se utiliza comúnmente para calcular el promedio de datos relacionados con velocidades, tasas y ratios, como la velocidad promedio de un viaje en automóvil o la tasa de retorno promedio de una inversión. Es siempre menor que la media aritmética, a menos que todos los valores del conjunto de datos sean iguales.

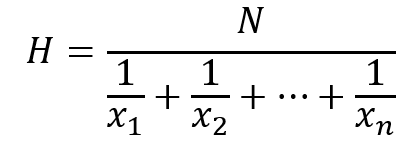
Fórmula de la media armónica

Medidas de variabilidad

Es una medida de la dispersión de los datos en una distribución, sea esta teórica o de una muestra. Miden la dispersión, desviación y oscilación.

Desviación media

Es la media aritmética de los valores absolutos de las desviaciones respecto a la media. Es una manera de describir la variación en un conjunto de datos. Nos ayuda a tener una idea de qué tan "extendidos" están los valores en un conjunto de datos.

Fórmula desviación media

Desvío

Es una medida de la diferencia entre el valor observado de una variable y algún otro valor, a menudo la media de esa variable. Signo (+) o (-) informan la dirección de la desviación.

Los valores de desvío o desvaición son muy altos.

La media aritmética no es representativa cuando…

Varianza

Media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística. Es una medida de dispersión. Eso significa que pretende capturar en qué medida los datos están en torno a la media. Mayor valor de esto, mayor dispersión y variabilidad.

Σ(Xi-𝝻)^2*fi/N

Fórmula de la varianza para distribución de frecuencias

Σ(Xi-media)^2/n

Fórmula de la varianza para datos simples

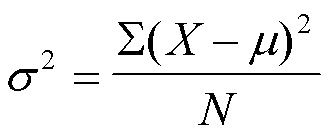
Símbolo de la varianza poblacional

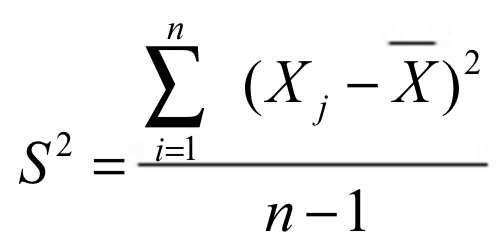
Símbolo de varianza muestral

Desviación estándar

Raíz cuadrada de la varianza, representa su valor lineal. Medida cuadrática de lo que se apartan los valores de su media. Sirve para comparar variables que están a distintas escalas pero que están correlacionadas estadísticamente y sustantivamente con un factor en común.

σ

Símbolo de desviación estándar poblacional

s

Símbolo de desviación estándar muestral

Coeficiente de variación

Este sirve como medida relativa de dispersión. Determina el grado de dispersión de un conjunto de datos relativo a su media. Comparación. Si nos da un valor muy grande con la media, se utiliza la mediana.

CV

Símbolo del coeficiente de variación poblacional

cv

Símbolo del coeficiente de variación muestral

Coeficiente de variación mayor al 30%

Coeficiente de variación es grande

Medidas de formas

Son unos indicadores que permiten describir una distribución de probabilidad según la forma que tiene. Sirven para determinar cómo es una distribución sin necesidad de representarla gráficamente. Nos muestran si una distribución de frecuencia tiene características especiales como simetría, asimetría, nivel de concentración de datos y nivel de apuntamiento que la clasifiquen en un tipo particular de distribución.

Momento

Son formulaciones matemáticas, que se definen como parámetros estadísticos, algunos de ellos cuales tienen amplia connotación dentro del estudio de curvas de distribución de frecuencias y más específicamente respecto del sesgo y de la curtosis.

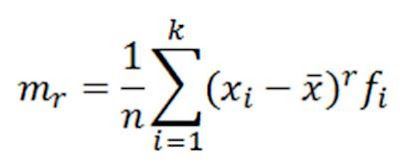
Fórmula para momentos

Momento 0

Siempre será igual a 1.

Momento 1

Este momento siempre será 0.

Momento 2

Este momento es igual a la varianza de distribición de frecuencias.

Momento 3

Con este momento se calcula el coeficiente de asimetría

Momento 4

Con este momento se calcula el coeficiente de Curtosis

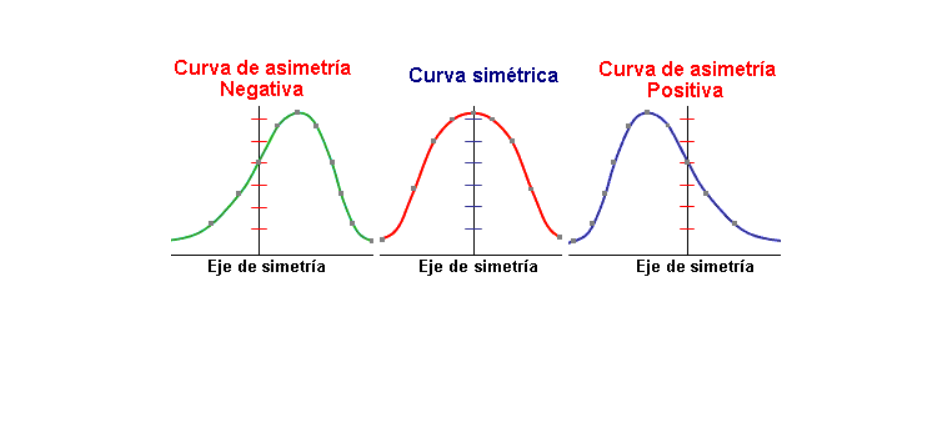
Asimetría

Se refiere a si la curva que forman los valores de la serie presenta la misma forma a izquierda y derecha de un valor central (media aritmética).

Distribución de datos sesgada

La distribución de datos no es simétrica y se extiende más hacia un lado que hacia otro.

M3/(σ)^3

Fórmula para coeficiente de asimetría

Coeficiente de Asimetría es menor a 0

La distribución de datos es asimétrica a la izquierda (negativa) cuando…

Coeficiente de Asimetría es mayor a 0

La distribución de datos es asimétrica a la derecha (positiva) cuando…

Coeficiente de asimetría es igual a 0

La distribución de datos es simétrica cuando…

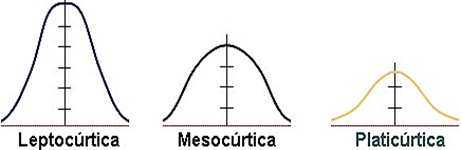
Kurtosis

Grado de concentración que presentan los valores alrededor de la zona central de la distribución. Cómo se agrupan los valores en torno a su media.

M4/(M2)^2

Fórmula coeficiente de curtosis

Forma platicúrtica

Coeficiente de curtosis es < 3

Forma Mesocúrtica

Coeficiente de Curtosis es = 3

Forma Leptocúrtica

Coeficiente de Curtosis es > 3

Que los datos son poco cambiantes, se concentran en la gráfica.

La forma leptocúrtica significa…

Que los datos están muy dispersos, son muy cambiantes.

La forma platicúrtica significa…

Estandarización

Es el proceso de ajustar o adaptar ciertas características para que los datos se asemejen a un tipo, modelo o normal común con el objetivo de que su tratamiento, acceso y uso sea más sencillo para los usuarios o personas que dispongan de ellos.

Puntuación estándar (P.E., zi)

Es un método de comparación de las posiciones relativas de dos o más elementos respecto al conjunto de observaciones. Devuelve el número de desviaciones estándar que la puntuación xi se desvía de la media.

Xi-Media/σ

Fórmula para la puntuación estándar

Puntuación directa

Puntuación definida por Xi/Valor puntual

Puntuación diferenciada

Es la distancia entre la puntuación directa y la media.

Medidas de concentración

Son medidas de reparto del total de la variable. Trata de definir si el reparto de los valores en la distribución es más o menos equitativo o si es desigual.

Coeficiente de Gini

Es una medida de la concentración de una distribución o equidad en el reparto de una distribución. es el método más utilizado para medir la desigualdad salarial. Es una herramienta analítica que suele emplearse para medir la concentración de ingresos entre los habitantes de una región, en un periodo de tiempo determinado.

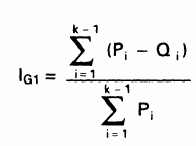
Fórmula del Coeficiente/Indice de Gini

Coeficiente de Gini = 0

En la distribución de los valores hay mínima concentración o equidistribución

Coeficiente de Gini = 1

En la distribución de los datos hay máxima concentración.

Medidas de asociación

Tienen el objetivo de definir si dos variables aleatorias tienen alguna relación y que tan intensa es.

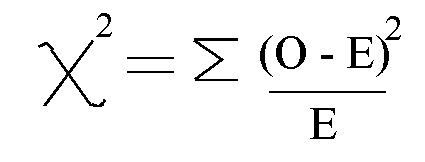
Coeficiente chi cuadrado (χ²)

Es un procedimiento estadístico utilizado para determinar si existe una diferencia significativa entre los resultados esperados y observados en una o más categorías.

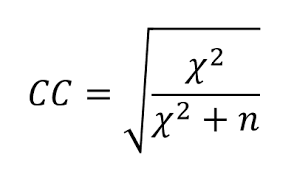
Coeficiente de contingencia (CC)

Indica si dos variables o conjuntos son independientes o dependientes entre sí.

Medidas de confiabilidad

Procedimientos que miden la fiabilidad o ausencia de errores de medida.

Alfa de Cronbach

Un coeficiente que toma valores entre 0 y 1, utilizado para saber cuál es la fiabilidad de alguna escala o test. La fiabilidad se define como la ausencia de errores de medida en un test o la precisión de su medición. Cuanto más se aproxime el valor al número 1, mayor será la confiabilidad del instrumento que se está tratando. Si se da un resultado negativo, esto denota un grado alto de inconsistencias dentro del instrumento