Mechanics - Model Answers

1. Draw & Explain a displacement time graph for a ball that is launched from the floor, thrown up into the air, reaches a maximum height, falls back down and bounces twice.

See diagram

• Displacement is positive at all time as the position of the ball is always above the starting point (positive vectors are upwards).

• As the ball moves upwards, it decelerates ( as it is moving in the opposite direction to the resultant force): the gradient of the graph, whcih represents the velocity, decreases.

• At the top of its journey, it has zero velocity: the gradient is zero.

• As it falls back down, it accelerates (as it is moving in the same direction as the resultant force): the gradient of the graph, which is the velocity, is negative as the direction has changed, and it increases as the ball accelerates.

• When the ball bounces, its displacement is momentarily zero.

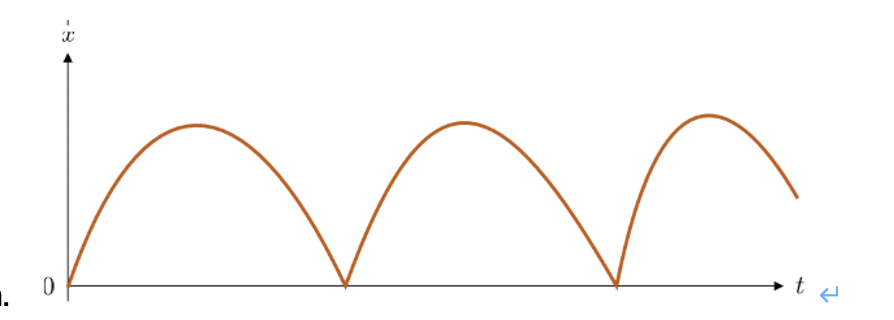
3. Draw & Explain a velocity time graph for a ball that is launched from the floor, thrown up into the air, reaches a maximum height, falls back down and bounces twice.

See diagram.

• The velocity starts high and positive when the ball is launched - positive vectors are upwards.

• The velocity decreases as the ball moves upwards, as the ball is develerating as it is moving in the opposite direction to the resultant force of weight.

• When the ball is at the top, the velocity is momentarily zero.

• The ball changes direction and the velocity becomes negative as the boy moves down (taking downwards and vectors are negative).

• The gradient of this graph, which is the acceleration, remains constant. Gravity is the acceleration, this remains constnat, as acceleration due to gravity is always constant and negative.

• When the ball bounces. it changes direction back to moving upwards in a very short amount of time: this is the almost vertical line, indicating high positive acceleration due to the high positive gradient.

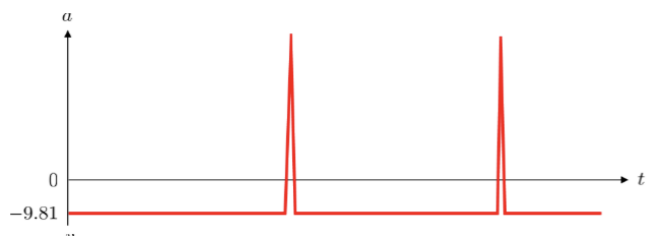
5. Draw and Explain the acceleration time graph for a ball that is launched from the floor, thrown up into the air, reaches a maximum height, falls back down and bounces twice.

SEE graph

• The acceleration is constant and negative for all of the ball’s flight.

• This is because the acceleration due to gravity is always -9.81ms^-2 (the only force that is acting is the weight) and it is negative as we have considered upwards vectors to be positive,

• When the ball bounces, it experiences a high positive acceleration for a very short time as the velocity is rapidly changing from negative to positive.

7. Explain the significance of the gradient and area under the line for a displacement time graph, a velocity time graph, and an acceleration time graph.

• From a displacement time graph: The gradient is Δs/Δt = v

  Area = N/A

• From a velocity time graph:

  The gradient is Δv/Δt = a

  The area under is displacement.

• From an acceleration time graph:

  Gradient = N/A

  The area under is velocity

8. Sort this list of quantities into scalar and vectors: force, acceleration, mass, time, velocity, KE, work done, speed, distance, displacement, momentum, gravitational potential energy.

Scalars:

• Mass

• Time

• Kinetic Energy

• Work done

• Speed

• Distance

• GPE

Vectors:

• Force

• Acceleration

• Velocity

• Displacement

• Momentum

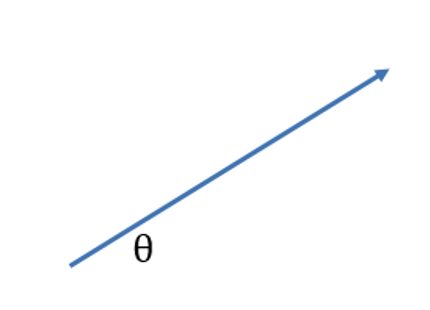
9. Draw a diagram illustrating how to resolve this vector into horizontal and vertical components. And label their magnitudes in terms of θ.

SEE diagram:

Vertical : sin

Horizontal: cos

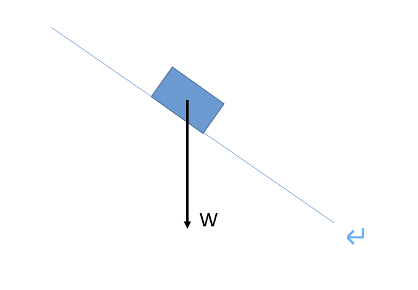
10. Draw a diagram to illustrate how to resolve this vector into components that are parallel and perpendicular to the plane.

Horizontal on the left of object: sin

Horizontal on the right of object : cos

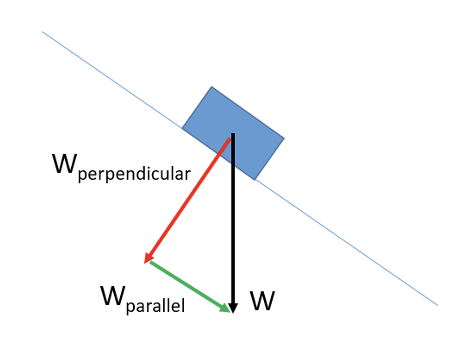
11. Draw a scaled vector diagram to illustrate the resultant force acting on this object. State its magnitude and direction above the horizontal.

Resultant force is 30 N, 50 degrees above the horizontal.

12. State Newton’s First Law.

An object will remain at constant velocity or stationary, if the resultant force is zero.

13. State Newton’s Second Law.

The resultant force acting on an object is equal to the mass of the object multipled by the acceleration it experiences in the direction of the resultant force.

14. State Newton’s Third Law.

When Object A exerts a force on Object B, Object B exerts an equal and opposite force on object A.

15. State the criteria that Newton’s Third Law pairs must satisfy.

• Act on different objects

• Be the same size

• Be the same type of force (e.g. Both gravitational / both electrostatic)

• Act in opposite directions

16. State the Newton’s Third law pairs for a person standing on the ground and draw the force arrow diagram for these.

• Force 1 = pull from Earth on person (weight)

• Force 2 = pull from person on Earth

• Force 3 = push from person on ground

• Force 4 = push from ground on person (reaction)

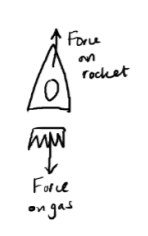
17. A rocket ejects gas backwards whilst in deep space. Explain, using Newton’s laws, what happens to the motion of the rocket.

• The rocket applies a force on the gas backwards.

• Due to Newton’s Third Law, the gas applies an equal and opposite force on the rocket forwards.

• The rocket experiences a resultant force, so due to Newton’s Second Law it accelerates forwards.

18. Define centre of gravity.

The centre of gravity of an object is a point where the entire weight of an object appears to act.

19. Define moment.

Moment = force x perpendicular distance between the line of action of the force and the pivot.

20. State the principle of moments.

The sum of the anticlockwise moments is equal to the sum of the clockwise moments for a system in rotational equilibrium.

21. Apply the principle of moments to solve this problem.

    A ladder is leaning against a wall. The uniform ladder has a mass of 40kg. Calculate the size of the force, F, required in order for the ladder not to fall.

1. Weight = mg = 40 × 9.81 = 392.4N

2. Uniform beam, so weight acts from centre of mass, 1m along the beam. (Vertically downwards force acting in the middle of the ladder).

3. Draw a dotted line carrying on from the line of action of the force.

4. Extend this line so a new perpendicular line to the line of action of the force can intersect with pivot (taking bottom of ladder as pivot).

5. Use trigonometry to crente equations for moment for each force, clearly stating whether moment is clockwise or anticlockwise.

Moment for weight force (anticlockwise moment):

M = 392.4 × 1cos35 = 321.4 Nm

Moment for F (clockwise moment):

M = F x 2sin35 = F x 1.147 Nm

6. Apply the principle of moments

   CM = ACM

   F x 1.147 = 321.4

   F = 280 N

23. Explain how the velocity changes throughout a skydive / a ball falling through a fluid.

1. Initially, the resultant force is weight.

2. F_R = W = mg, so a = g due to Newton’s Second Law. So the person/ball accelerated at g = 9.81 m/s^-1, the acceleration due to gravity.

3. As their speed increases, air resistance increases.

4. This causes the resultant force to decrease.

5. Until air resistance = weight, and the resultant force is zero.

6. At this point the acceleration is zero due to Newton’s First Law - they are falling at terminal velocity.

24. Conservation of energy.

Sum of energy remains constant before and after a collision.

25. A student investigated the behaviour of a pendulum. The student used a ‘spring gun’ to fire a small sphere of modelling clay at the wodden pendulum bob, as shown in Figure 1. The clay stuck to the pendulum bob, which swung to one side, as shown in Figure 2,.

Explain how the conservation of energy applies to this situation. Consider the situation from the moment that the spring gun is released, to when the pendulum bob is at its maximum height. [7]

• The spring gun stores Elastic potential energy.

• This is transferred to the kinetic energy store of the modelling clay.

• The clay then moves to the pendulum bob and collides inelastically with it.

• Some of the KE store of the clay is transferred into gravitaional potential energy.

• At the maximum height, all of the KE has become gravitatiional potential energy.

26. Define Work done.

Work done is force x displacement in the direction of the force (NOT LINE OF ACTION OF FORCE - M)

27. Define efficiency.

• (Useful work done / total work done) x 100

• (Useful energy output / total energy input) x 100

• (Useful power output/ total power input) x 100

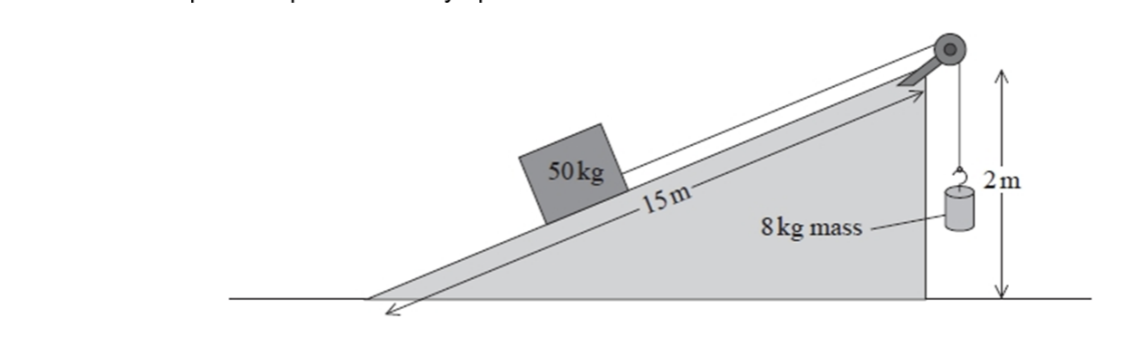
28. The machine used a slope of height 2.0m and length 15m to move the box. The box was connected to an 8.0 kg mass by a rope over a pulley as shown. As the 8.0 kg mass fell, the box moves up the slope at a steady speed.

a) Describe what the total work done on the 50 kg mass is.

• The total work done is the change in Gravitational Potential Energy of the 8kg mass. This mass can only move downwards by 2m, so this is 8 × 9.81 × 2. This is the same as the tension in the string (equal to the 8kg weight as the system moves at a constant velopcity) x the displacement in the direction of that tension force, 2m up the slope.

• This total work done goes into doing two things :

  a) Raising the box up - doing work against gravity to increase its GPE.

  b) And doing work against friction, transferring energy to the surroundings.

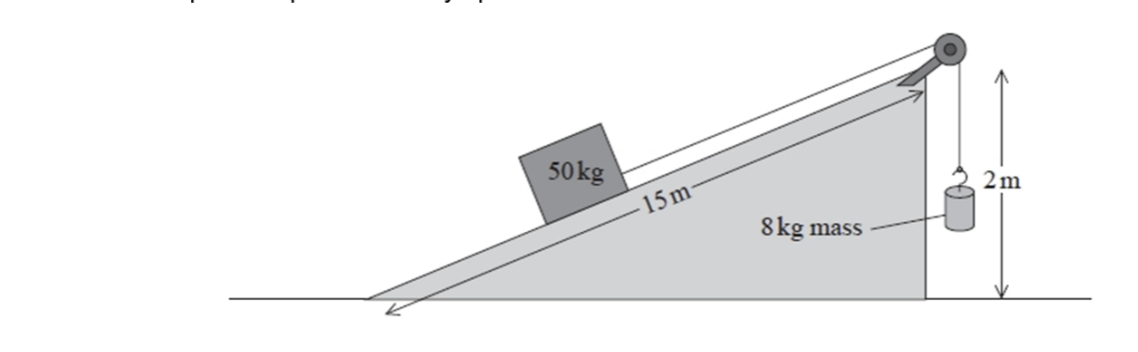
28. The machine used a slope of height 2.0m and length 15m to move the box. The box was connected to an 8.0 kg mass by a rope over a pulley as shown. As the 8.0 kg mass fell, the box moves up the slope at a steady speed.

b) Describe what the useful energy output is.

• The useful energy output is the work done on the 50 kg box against gravity.

• This is the gain in GPE of the 50 kg box.

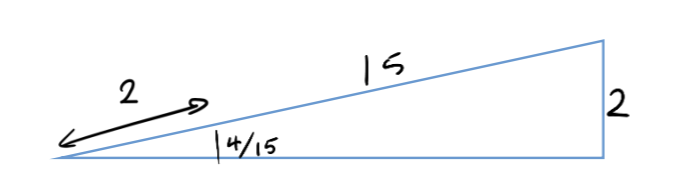
• The vertical distance it is raised by, is found using similar traingles to see that this is 4/25.

• So the change in GPE of the 50 kg box is = mgh = 50 × 9.81 × 14/15. (This can also be found by doing work done against gravity = weight x displacement in the direction of the force e.g. mg x 2 × 2/15).

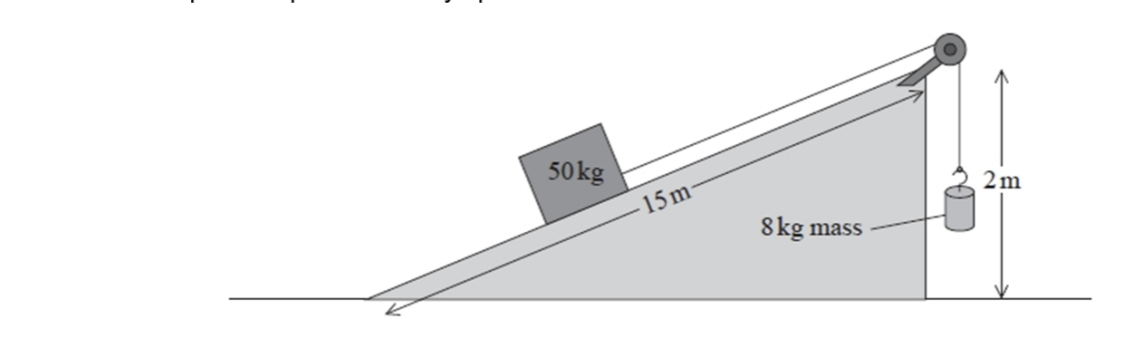
28. The machine used a slope of height 2.0m and length 15m to move the box. The box was connected to an 8.0 kg mass by a rope over a pulley as shown. As the 8.0 kg mass fell, the box moves up the slope at a steady speed.

c) Explain how you could find the energy dissipated by the system.

• There is work done against friction, which transfers energy to the surroundings.

• This can be calculated using: work done against friction = total work done (GPE change of 8kg mass) - work done against gravity on the box.

29. Conservation of momentum.

The vector sum of the momenta before a collision is equal to the vector sum of the momenta after a collision, provided no external forces act.

30. Explain how conservation of momentum applies to a situation where an object ejects gas and starts moving. e.g. a rocket leaves the surface of the Earth.

• Before the gas is ejected, the total momentum of the system is zero.

• As no external forces act, the total momentum after the explosion is zero.

• When the gas is ejected, the gas experiences a reultant force downwards.

• As force = rate of change of momentum, the gas’s momentum increases in the downwards direction.

• Therefore the rocket must also experience a change in momentum equal and opposite to the gas’s momentum (due to Newton’s third Law, the force is equal and opposite).

• So it has momentum upwards that is equal in size and opposite in direction to the gas’s momentum - the vector sum of momenta is still zero.

31. Impulse.

Impulse is the resultant force x time (= change in momentum).

32. Linear momentum.

Linear momentum = product of mass and velocity.