CSC236 recursive runtime 2

Bottom heavy recurrence

Where majority of the “steps”, runtime come from the lower levels of recursion 

b^d < a

T(n)∈Θ(n^log_b​ a)

Example: Think of a giant tree orchard, where every small branch sprouts many new branches. Most of the fruit is at the bottom of the tree, so the lower branches do all the work

Balanced recurrence

The work around each level of recursion is roughly the same everything is around equal

b^d = a 

T(n)∈Θ(n^d logn)

Ex: Imagine a factory assembly line — every station contributes equally to the final product. No single station (level) dominates

Top-heavy recurrence

Most work done top of recursion tree, deeper levels do little

a<b^d

T(n)∈Θ(n^d)

Ex: Think of a boss-heavy project — the manager (top) does almost all the work, and the employees (lower levels) just follow instructions

Number of leaves = n^(log_b a)

Each recursive call decreases the size by n / b for k times meaning it splits into “a” smaller sizes

If you keep going till base case you get n^log_b a

Ex:

Imagine a tree where every branch splits into a branches.

If the tree height is log_b n ​, the bottom-most branches (leaves) are n^log_b a

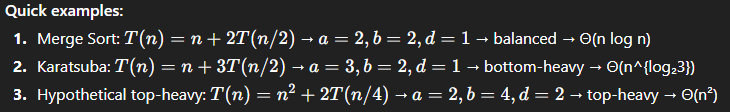
Simplfied time recurrence

n^d work outside recursion

aT(n/b) work done by recursion

Think of solving a big project:

• n^d → Work at this level (outside recursion):

  • This is the work you do yourself before delegating.

  • Analogy: You’re the project manager making plans, setting up tools, or merging the results at the end. The bigger the project (n), the more time this takes.

• a → Number of subprojects you delegate:

  • You break the project into a smaller teams.

• n/b → Size of each subproject:

  • Each team gets a piece that’s 1/b the size of the original.

• T(n/b) → Work done by each team recursively:

  • Each team does the same process on its smaller task: do their work (n^d for that level) + delegate to smaller sub-teams.

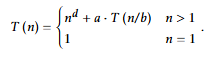
What is the recurrence for normal multiplication?

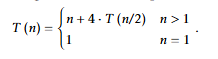
What is the recurrence for Karatsuba’s algorithm?

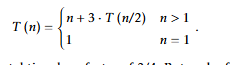
Why is it n²? for normal multiplication

it grows by a factor of 2 each level of tree

Why does removing 1 recursive call change the Θ so much?

It’s bottom heavy

Removing just 1 recursive call drops the branching factor from 4 → 3

What does n^(log₂ 3) mean?

just the number of leaves in the recursion tree

How do I know if the recurrence is bottom-heavy, balanced, or top-heavy?

• a = number of recursive calls

• b = factor by which the problem size shrinks each level

• d = exponent of the work done outside recursion

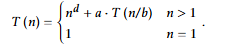
a > b^d

b^d < a = top heavy : The manager at the top does most of the work; the sub-teams don’t contribute muc

a = b^d

b^d = a : balance : Each level of the project (top, middle, bottom) contributes equally, like a factory assembly line

b^d > a 

b^d > a = bottom heavy : Lots of teams are working at the smallest subprojects; most work happens at the bottom