Maths Complex Numbers

Imaginary Numbers

We denote imaginary numbers with the letter I

Complex Numbers

A complex number has both real and imaginary parts

Z = x +iy

• x = Re(z)

• y = Im(z)

Addition And Subtraction Of Complex Numbers

For addition and subtraction you just add or take the real parts together and add or take the imaginary parts together

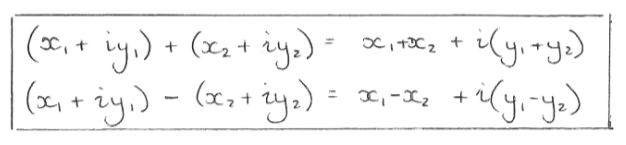
Multiplication Of Complex Numbers

Multiply by expanding brackets, the I² part becomes a number using I² = -1, I stays and it all becomes a complex number again.

Complex Conjugate

Every complex number has another associated with it called it’s complex conjugate

• Basically you just swap the sign before the imaginary number

Note multiplying a complex number by it’s conjugate always produces a real number

Division Of Complex Numbers

Times by the (conjugate/conjugate) and then simplify

• This gives a real number on the bottom

Argand Diagram

A graphical representation of complex numbers on a two-dimensional plane, where the x-axis represents the real part and the y-axis represents the imaginary part.

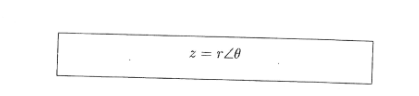
Polar Form

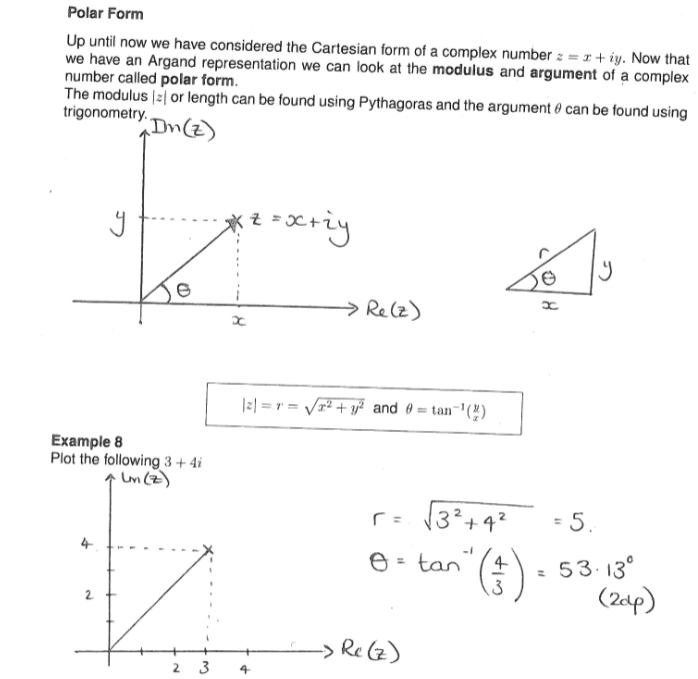
Now we have Argand representation we can look at the modulus and argument of a complex number called polar form.

The modulus |z| or length can be found using Pythagoras and the argument (angle) can be found using trigonometry.

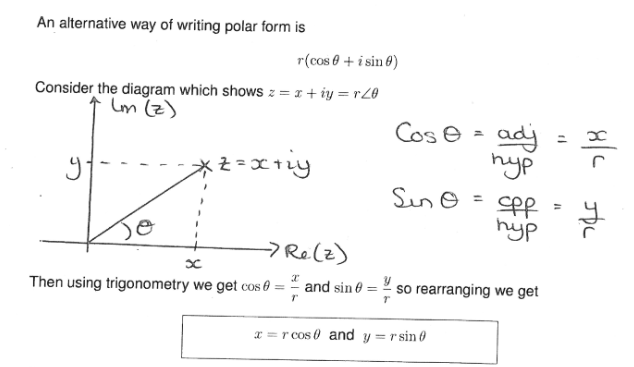
Alternate Polar Form

x = r cos (angle) and y = r sin (angle)

Multiplication And Division In Polar Form

If we have two complex numbers in polar form

Reciprocal Of A Complex Number

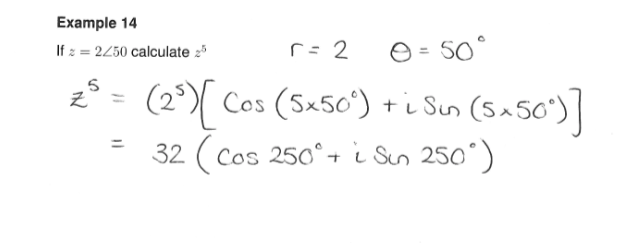
De Moivre’s Theorem

Used when we have a complex number raised to a power

Complex Roots Of Equations

Division to find roots

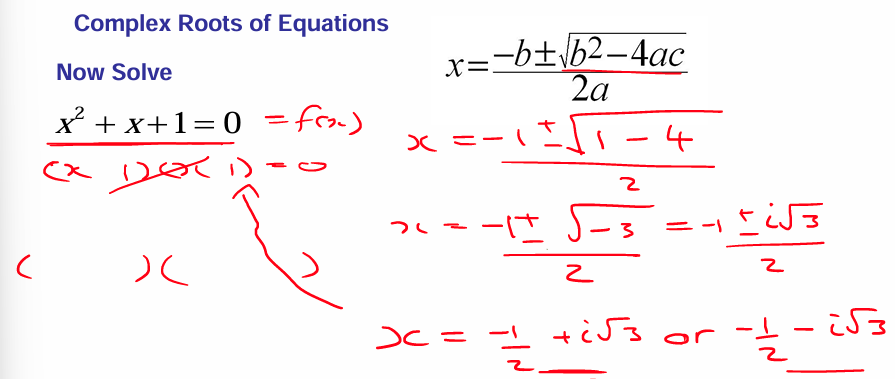
Modulus And Argument Form

Exponential Form

Angle must be in radians

All In One

Trigonometry Identities

Multiplication In Polar Form

Hyperbolic Functions