Applied econometrics lecture 15 causality

Non-random sampling

where the sample is not drawn randomly from the population of interest

We assume random sampling

causal Qs and splitting the problem into 2

Identification

Statistics

splitting the problem into 2 - identification

What could we learn about the parameters we care about (causal effects) if we had the observable data for the entire population

• Need to make assumptions about how observed outcomes relate to outcomes that would have been realized under different treatments

splitting the problem into 2 - stats

What can we learn about the full population that we care about from the finite sample that we have?

• Need to understand the process by which our data is generated from the full population

Indicator for treatment

D_i

Outcome under treatment

Y_i (1)

Outcome under control

Y_i (0)

observed outcome

D_i Y_i (1) + (1 - D_i) Y_i (0)

When D_i = 1 we only observe Y_i (1)

Example estimator

Example estimand

Example target parameter

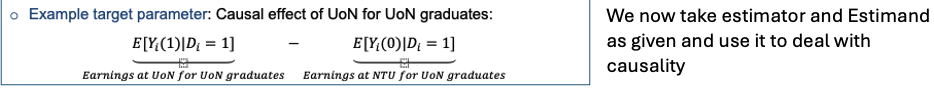
We cant assume the 2nd term is equal to earning as NTU for NTU grads - due to selection bias / omitted variables

(other ways that affect earnings (regardless of where they went to uni))

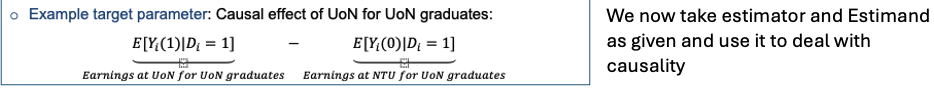
Individual treatment effect (TE)

Y_i (1) - Y_i (0)

Average treatment effect (ATE)

average causal effect between group the unit is in

(affect of attending UoN instead of NTU)

E( Y_i (1) - Y_i (0) )

Effect of treatment on treated (TOT)

average causal effect of group among those who are part of the group

(of attending UoN among those who attended UoN)

E( Y_i (1) - Y_i (0) | D_i = 1) = E( Y_i (1) | D_i = 1) - E( Y_i (0) | D_i = 1)

Selection bias

Does having health insurance make you healthier

As the extra characteristics are statistically different between men with HI and without HI, it makes us believe that the outcome will be different for the 2 populations

The observed difference could come from the selection bias term

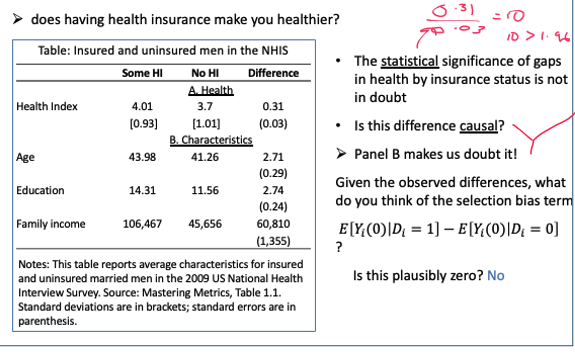
Random assignment and selection bias

When treatment status is randomly assigned, selection bias disappears

The potential outcome of the people that are not treated without treatment is the same as the potential outcome without treatment of the people who are treated.

Random assignment and the Uni example

Suppose that UoN & NTU administration randomized who got into which uni

Since university is randomly assigned, the only thing that differs between UoN and NTU students is the university they went to

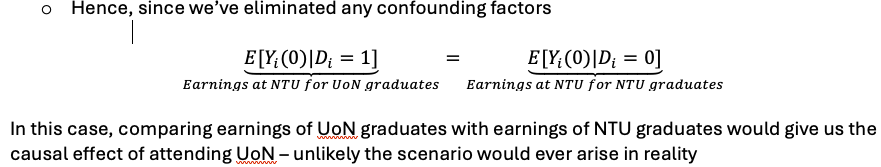
Random sampling vs Random assignment

Random sampling

• facilitates statistical inference about population parameters, causal or otherwise

• We generally assume it holds

Random assignment

• supports causal inference, that is, comparisons of potential outcomes free of selection bias

• we achieve with RTCs

  • RTCs immoral in many cases

Omitted variable bias (OVB)

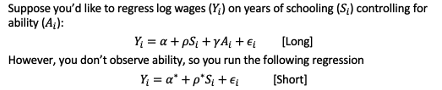
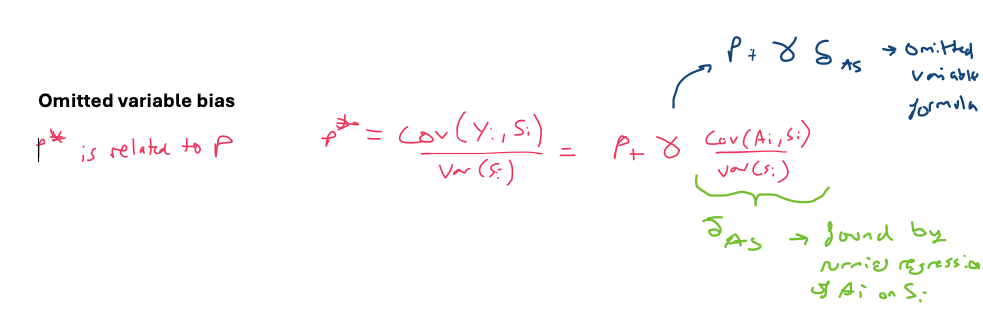
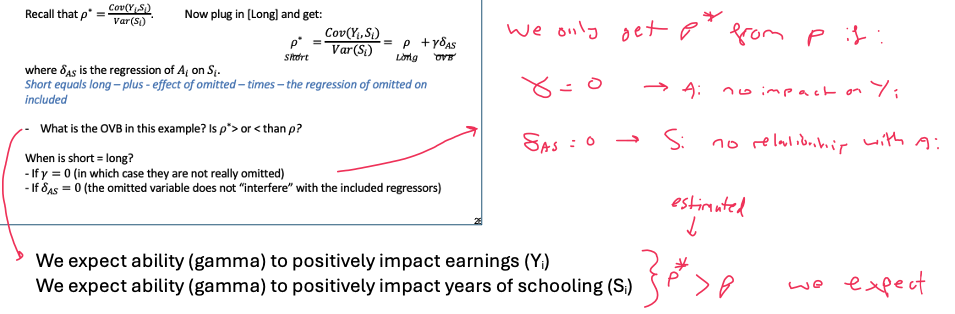
using OVB formula to investigate selection bias

The OVB formula is true for any short vs long regression comparison

Why would we want to run a long regression as opposed to a short regression:

• Because the potential outcomes ( Y_i (0)’s ) are likely different between the treated and the untreated

• Regression with the right controls reduces, and maybe even eliminates, selection bias arising from unbalances in Y_i (0)’s

Removing selection bias by controlling for OVB

By controlling for the only omitted variable (correlated with our explanatory), we can recover the treatment of the treated → we remove selection bias

Conditional independence assumption

When we have many variables, it is sufficient that D_i is ‘randomly assigned’ conditional on x, to recover causal parameter of interest

D_i ⊥ Y_i (…) | X_i

⊥ - conditional on

Sometimes (rare in reality) that by controlling for the right X_i’s it is sufficient to recover causal parameters of interest