Insertion Sort

more efficient

Insertion Sort

• Take values one by one from input array

• Insert into sorted array in correct order

In-Place Algorithm

Insert values into a sorted sub-array instead of completely new array

In-Place Algorithm Code

class InsertionSort {
   static void insertionSort (int[] array) {
      for (int i = 1; i < array.length; i++) {
         int j = 1;
         //swap array[j-1] and array[j]
         while (j > 0 && array[j-1] > array[j]) {
            int tmp = array[j-1];
            array[j-1] = array[j];
            array[j] = tm[;
            j--;
         }
      }
   }
}

Correctness Analysis

Invariant (for 1 ≤ i < length): 

• At the end of phase 𝑖, the first 𝑖 + 1 entries of the array are sorted (i.e., in increasing order)

Correctness:

• Prove invariant 

• Invariant for 𝑖 = length − 1 implies that the algorithm is correct

Worst-Case Time Complexity

Operation Counting:

In each phase 𝑖 (for 1 ≤ 𝑖 < length): 

• At most 𝑖 comparisons 

• At most O(𝑖) elementary operations

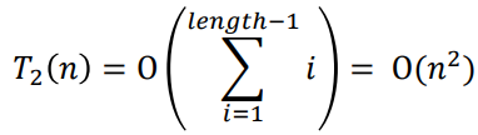
Analysis Summary

• Best case - O(n) - only for an already sorted array (as it never enters while loop)

• Average case - O(n^2)

• Worst case - O(n^2)

• In-place - yes