biostats final

parameter

quantity describing entire population

estimate

inferring unknown parameter from sample data

3 major goals of stats

estimate characteristics of pops

objectively answer scientific questions

describe degrees of uncertainty in scientific findings

variable

charcateristic measured on individual drawn from population

properties of good sample

ind

random

sufficiently large

random sample

each member of pop has equal and ind chance of being selected

sample is representative of the population

effects of sample size increasing

SD will become more accurate but will not systematically directionally change

SE will become smaller/narrower

1 numerical graph

histogram

2 numerical graph

scatter plot

1 categorical graph

bar graph

2 categorical graph

grouped bar graph

1 numerical 1 categorical graph

multiple histograms, dot/box plot

when is mode useful

in voting/surveys

when to use mean or median as measure of average

usually use mean but if outliers exist, use median

variance

average of the squared differences from the mean

SD

square root of variance

measure of inherent variability among individuals

coefficient of variation

SD/mean x 100

SE

variability between samples

most dangerous eq

SE

if sample size is small, SE appears more significant than it actually is. Small sample sizes can produce extreme values that can be misinterpreted

confidence interval rule of thumb

mean ± 2SE prpvides rough estimate of 95% CI

what does 95% CI mean

we are 95% confident that the true population mean lies within the 95% confidence interval

what happens to confidence interval as sample size inc

gets narrower

pseudoreplication

error that occurs when samples that are not independent are treated as though they are

characteristics of normal dist

• symmetric around mean

• about 2/3 of random samples are within 1 SD of the mean

• about 95% of random samples are within 2 SD of the mean

• mean=median=mode

  • bell shaped

standard normal distribution characteristics

mean=0

SD=1

standard normal deviate

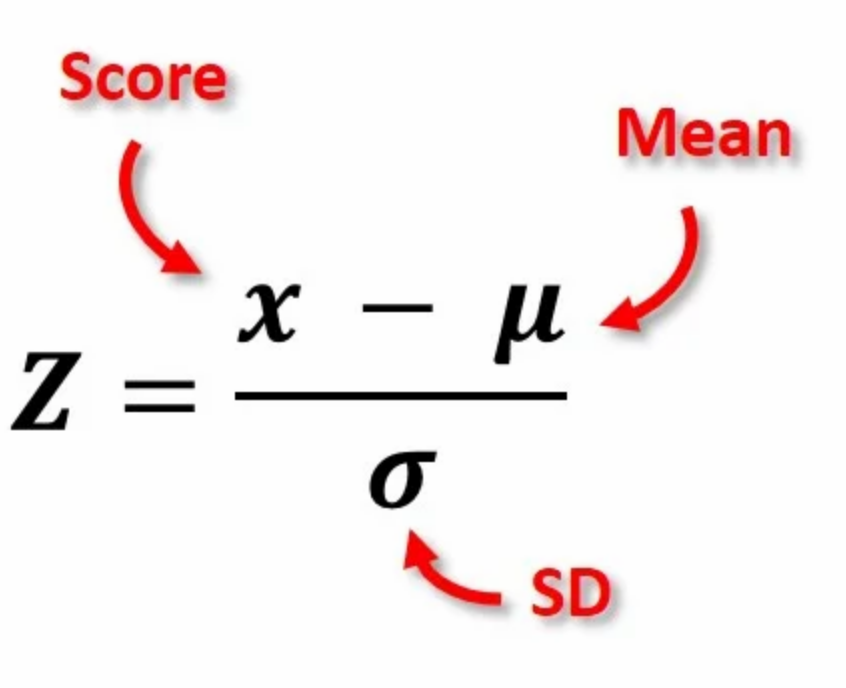
CLT

in a large sample, the mean of samples approaches a normal distribution regardless of if the population’s distribution is normal or not

how is t distribution different than z distribution

probailities based on a sample so need to account for greater uncertainty

• confidence intervals wider and more probaility in the tails b/c only have estimates of mean and SD

DF

number of observations = # of parameters

1 sample t text

compares mean of random sample w population mean

1 sample t test assumptions

random sample

independent measurements

varibale is normally distributed

how is 1 sample t test robust

CLT

paired t test

1 sample t test on differences between pairs

why is paired t test good

allows you to account for extraneous variation; greater statistical power

paired t test assumptions

random sample

each pair of data is independent

the diff between the pairs is normally distributed

paired t test robust

CLT

paired t test DF

#pairs - 1

2 sample t test

compares means of 2 samples

2 sample t test assumptions

random

independent

normal distribution

equal variance

equal sample size

2 sample t test robust

performs adequately if diff in SD is 3 fold or less and sample size is moderately large and sample size is similar in both groups

unequal variance/welch test

adjusts for very unequal variances

assumptions for welch

same as 2 sample but no equal variance

why not just always use welch instead of 2 sample t test

less statistically powerful

robust definition

test performs adequately even if assumptions aren’t met exactly

Q-Q plot

straight line means perfectly normal

informal normality checks

histogram and Q-Q

leptokurtic

too pointed

platykurtic

too flat

formal tests for normality

shapiro-wilks (n<50)

kolmogorov smirnow (n>50)

steps if parametric assumptions are violated

evaluate outliers

transform data

non-parametric test

positive skew transformation

slight: square root

moderate: ln or log

extreme: inverse

transform negative skew

first try square and if that fails

reflect data so it is now pos skewed and then use the pos transformations

backtransforming

backtransform important parameters like mean and SE/ 95% CI

DONT BACKTRANSFORM SD

when transformations don’t work

use non-parametric tests

non-parametric tests have…

fewer assumptions about shape and spread of data but are less statistically pwoerful

non-parametric version of 2 sample t test

mann-whitney u test

mann-whitney u test

converts data into ranks and tests for difference between medians

mann0whitney u test assumptions

similar shape and variance

non parametric test for paired and 1 sample

wilcoxon signed rank test and sign test

wilcoxon signed rank test

test difference between sample median and hypothesized median

turned diff data into ranks

wilcoxon signed rank test assumptions

data are symmetric around the mean

sign test

tests diff between sample median and hypotheiszed median

turned differences into +1 and -1

sign test assumptions

none

low statistical power

type 1 error

incorrectly rejecting the null hypothesis

populations not diff but saying they are

p value

estimate of likelihood of committing type 1 error

type 2 error

failure to reject the null hypothesis even though it is false

populations are different but saying they arent

ANOVA

1 categorical variable (2+ groups_) and 1 numerical value

example of ANOVA`

effect of 3 drugs and a placebo on blood pressure

what does anova compare

mean of 2+ groups

null hypothesis of ANOVa

all means are the same; there is no difference

alternate hypothesis for anova

there is at least one difference

anova assumptions

same as 2 sample tt est

anova robust

same as 2 sample t test

CLT and 3 fold

anova f statistic

F= s² between groups / s² within groups

when F=1

groups come from same population

when F>1

groups come from diff populations

degrees of freedom for ANOVA

1: k-1 = # groups -1

2: n-k= # observations = # groups

why not just do multiple t tests instead of ANOVA

-p value no longer representative of type 1 error

large probability of erroneous results

multiple comparisons would lead to too many type 1 errors

what to do after anova shows there is a diff

tukey test

why do we need tukey test

need to see WHICH groups are diff form each other

tukey test

compares all groups and determines which pairs are different

HSD

honestly significantly difference

why is tukey test important

protects us from making false conclusions due to many comparisons

tukey test assumptions

same as 2 sample t test

fixed effects

• constant across treatments

random effects

• not constant; size of effect varies within groups

E.g. testing 4 drugs and their speeds of recovery

fixed: care about specific drugs and the dosage that each person in each drug treatment group gets

e.g. testing dosage of drug A on speed of recovery

Fixed; care about particular dosage

e.g. compare GPA of students from wealthiest 10% and poorest 10% if families from 45 random schools

random effect; top and bottom 10% vary by school district

e.g. survey of patients about drug use vs. recovery time

random; low med high dosage groups but still variation in dosage in each group

random effects assumptions

same as 2 sample t test AND

• groups are from random sample

  • group means are normally distributed

welch’s ANOVA

used instead of ANOVA if variances are VERY different

welch’s anova assumptions

• random

• independent

  • normally distributed

• similar sample sizes

post hoc test used for welch’s anova

games-howell post hoc test

games- howell post hoc test

like tukey test but handles unequal variances

games-howell assumptions

same as welch’s anova

• random, independent, normal dist, similar sample size

non-parametric ANOVA

kruskal-wallis

kruskal wallis test assumption

similar shape and variance (like mann whitney U)

null hypothesis of kruskal wallis

all medians and distributions are equal

alterante hypothesis kruskal wallis

all medians are not the same; at least one group is different