Calculus BC

Unit 1

Limits

Limit exists if

the left and right hand side limits are equal

*

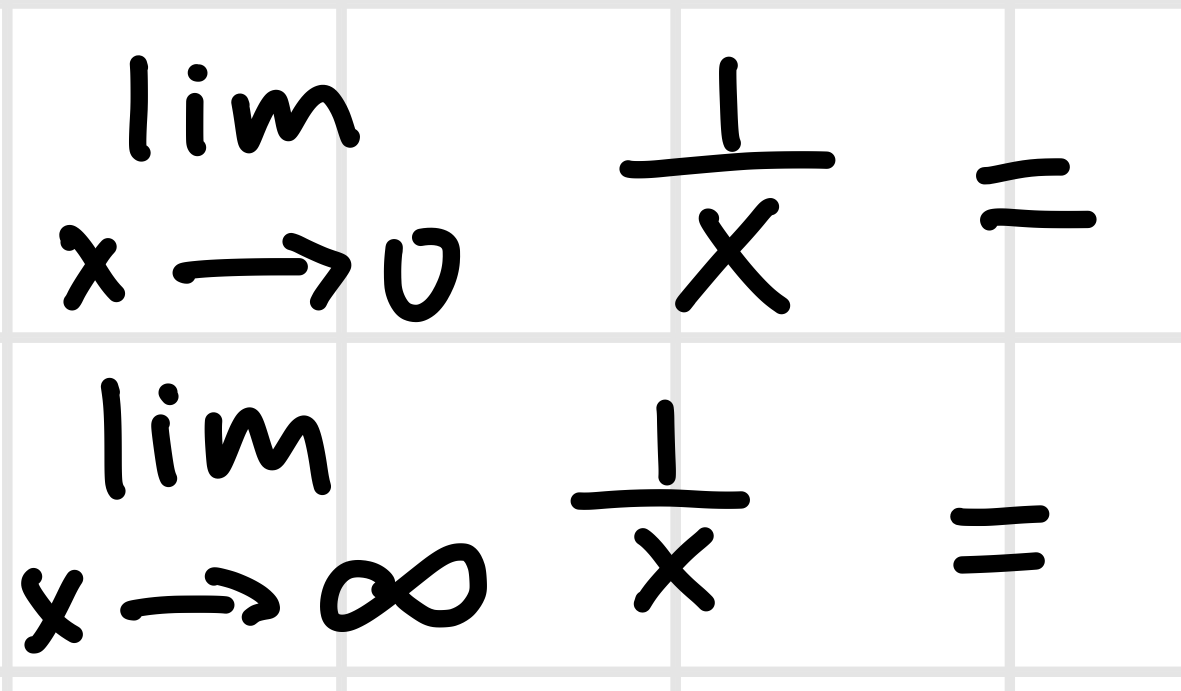
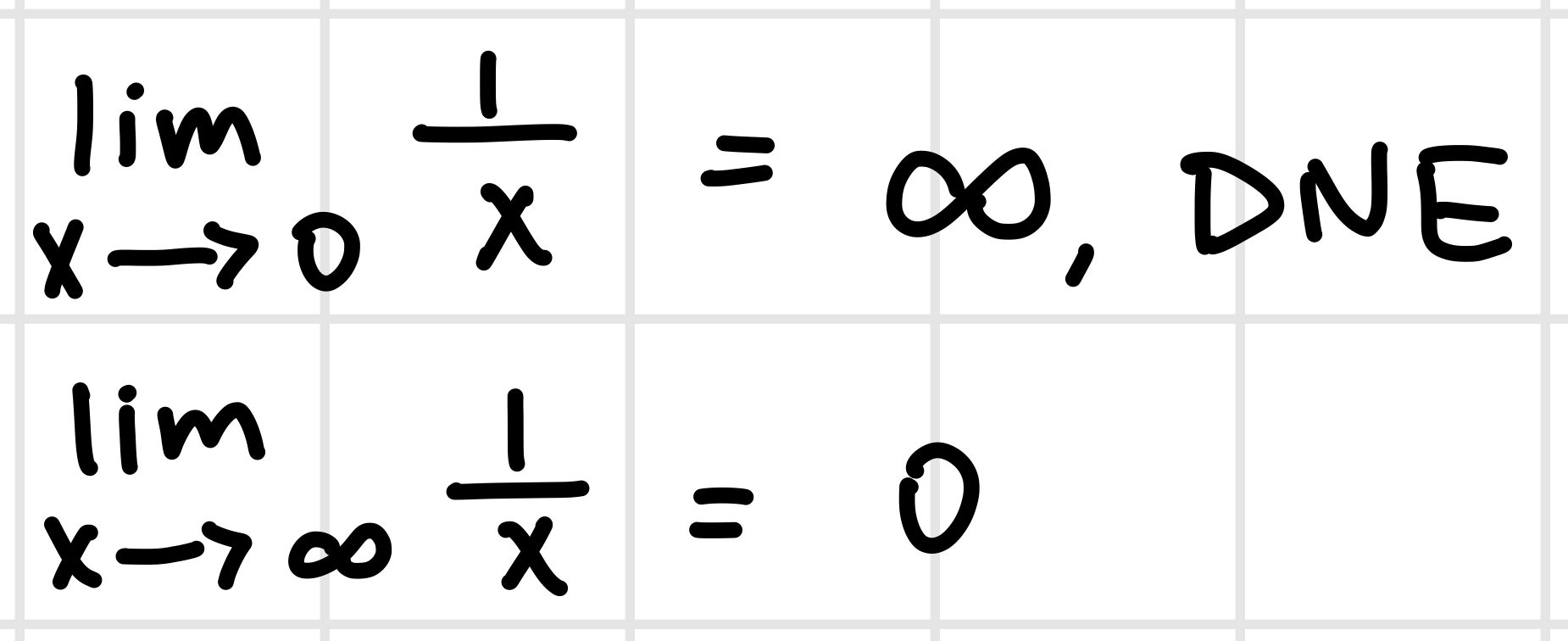
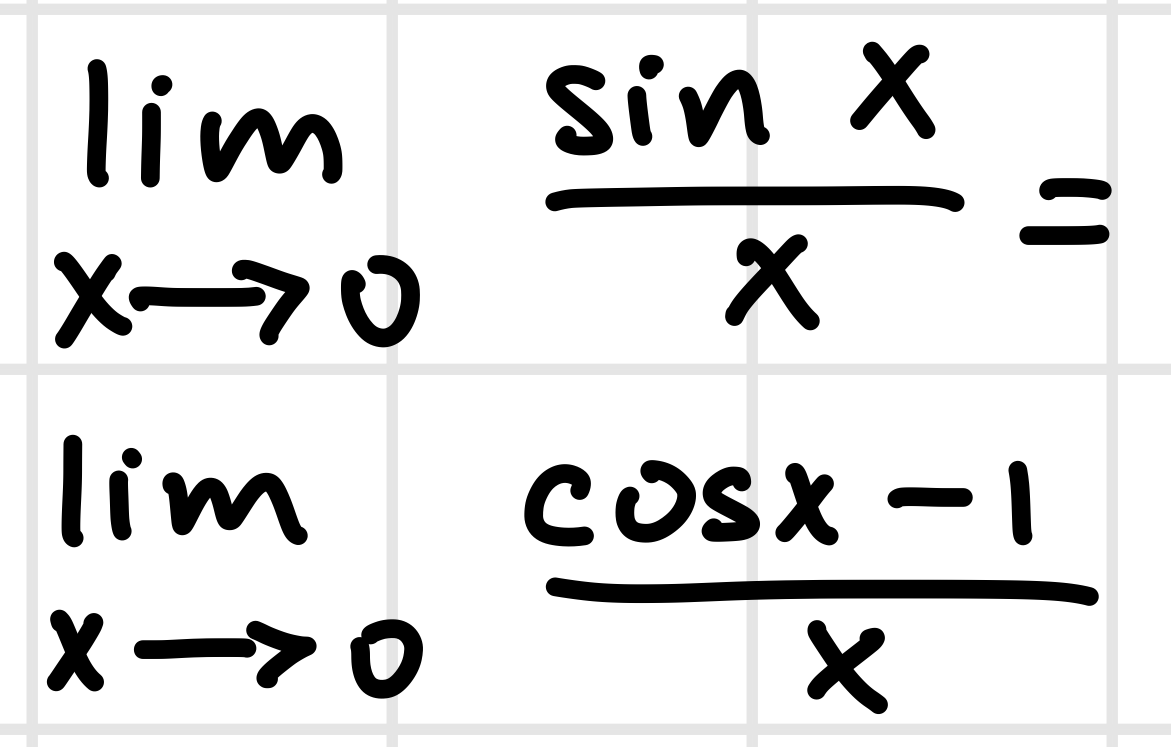
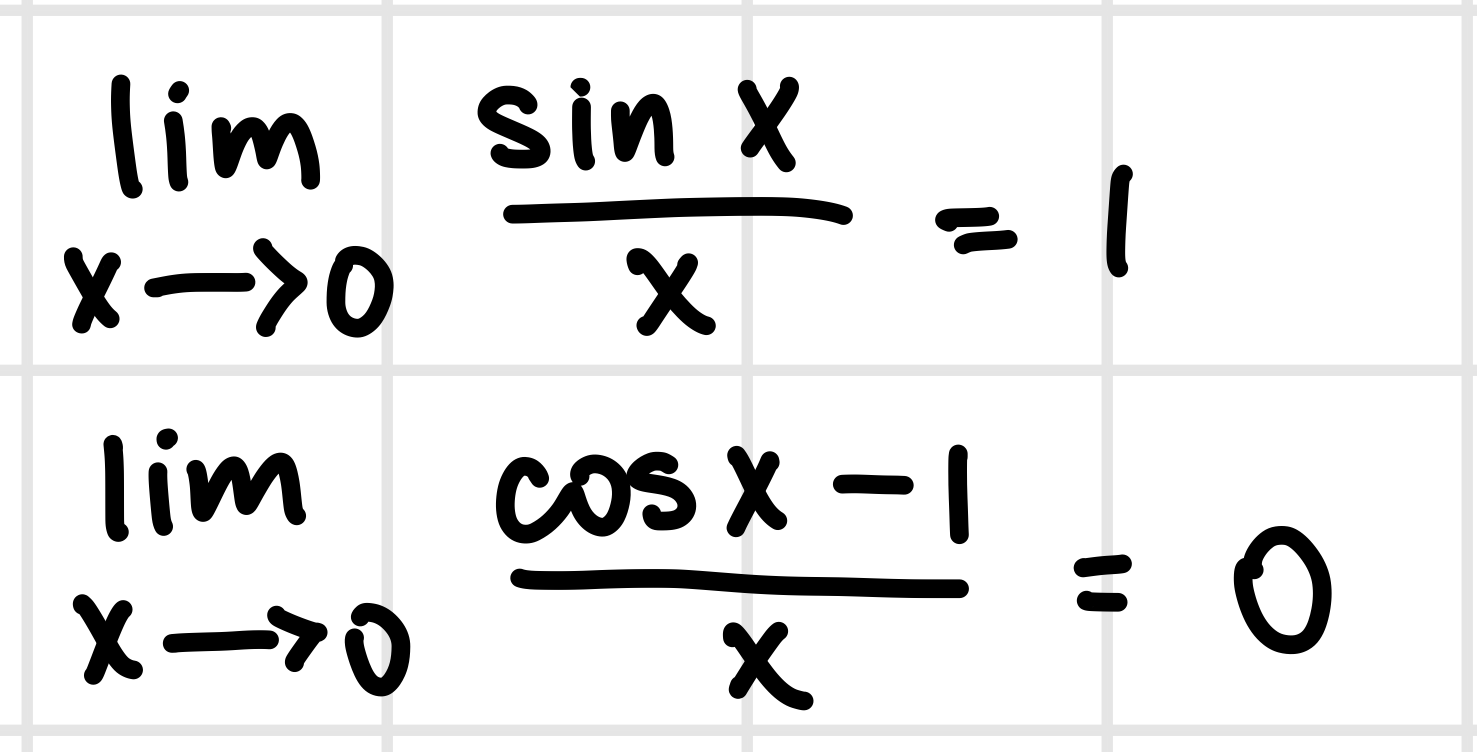
Horizontal Asymptote Rules*

Compare degrees of numerator and denominator

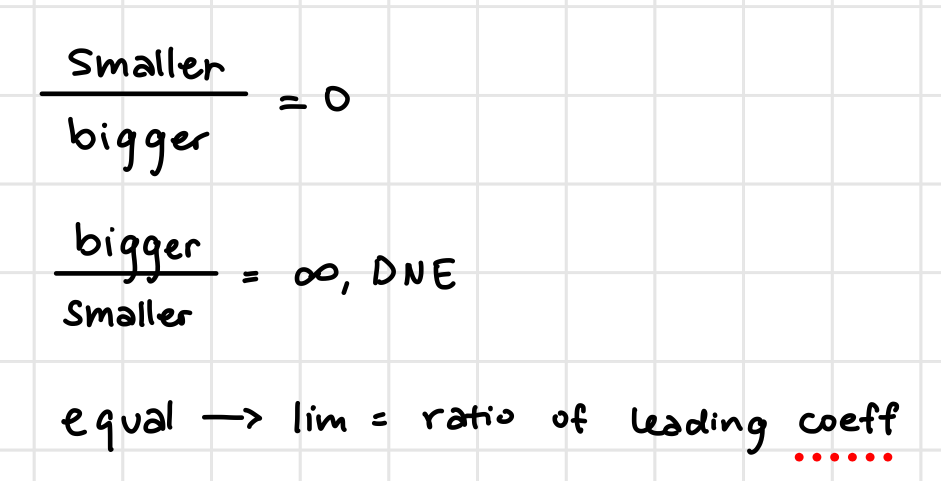
Three Types of Discontinuities*

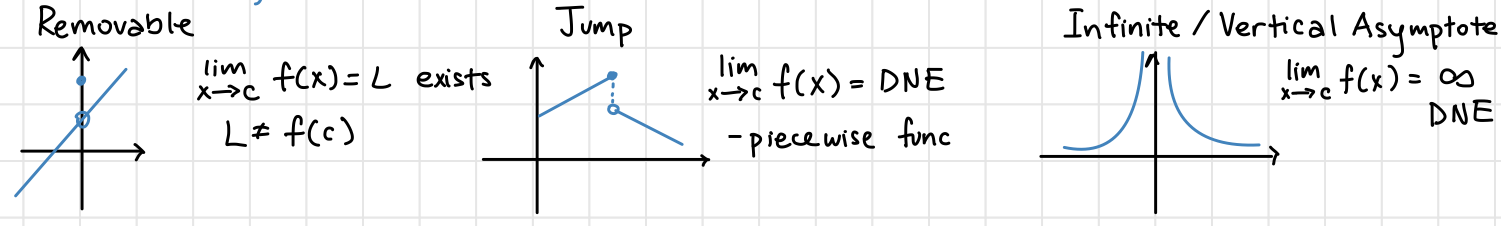
Intermediate Value Theorem

If a function is continuous on closed interval [a, b], and takes on values f(a) and f(b), then it takes on every value between f(a) and f(b) at least once.

Squeeze Theorem

if g(x) <= f(x) <= h(x), and the limits of g(x) and h(x) as x approaches a particular value are equal, then the limit of f(x) as x approaches that value is also equal.

Unit 2

Differentiation

Average Rate of Change (AROC)

The slope of the secant line between two points on a graph

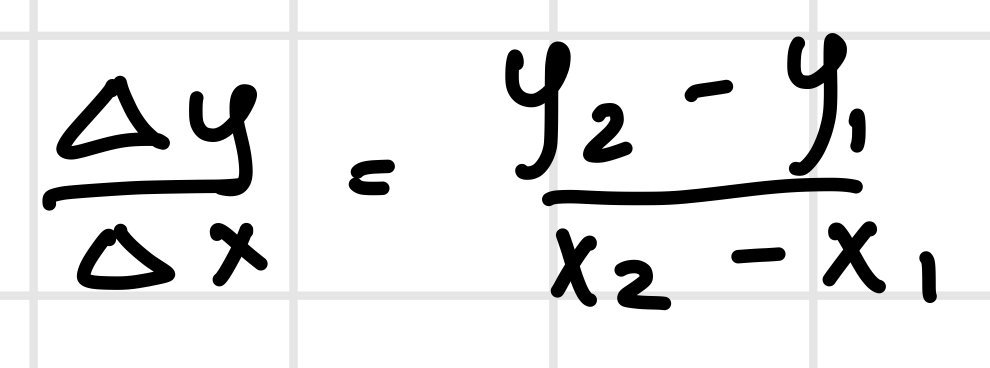
Instantaneous Rate of Change (ROC)

Slope of the tangent, lim of the secant line as the interval approaches zero.

Derivative Principle Formula

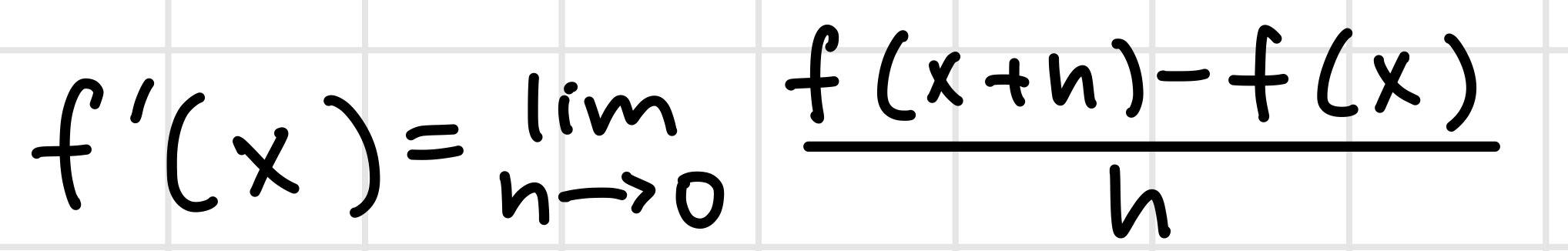
Constant Rule

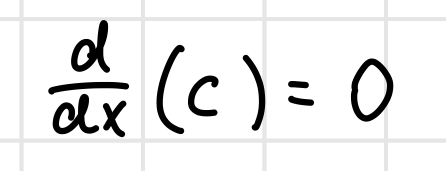
Constant Multiple Rule

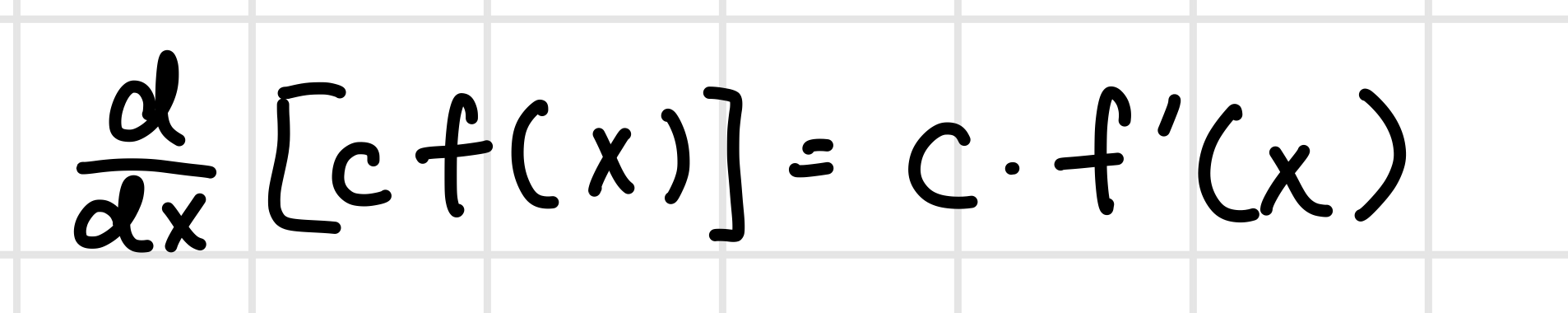
Power Rule

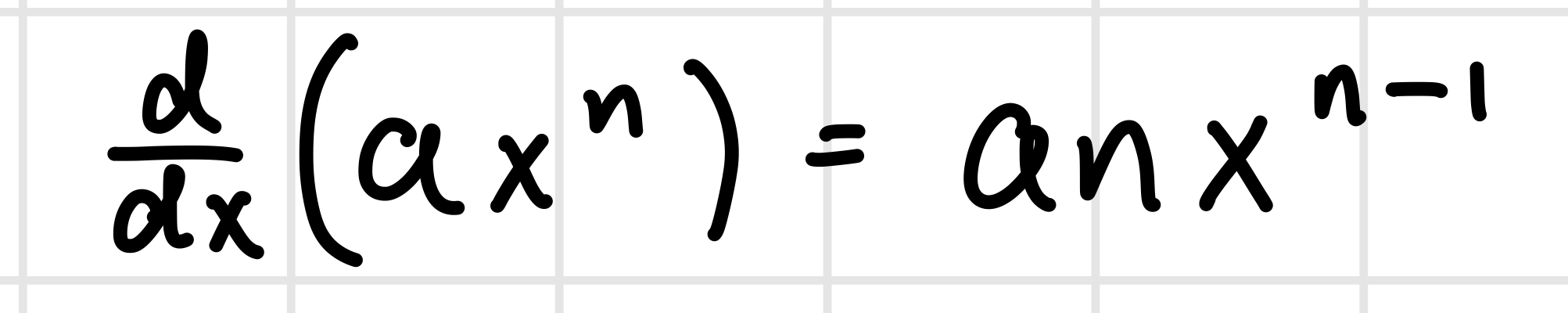
Product Rule

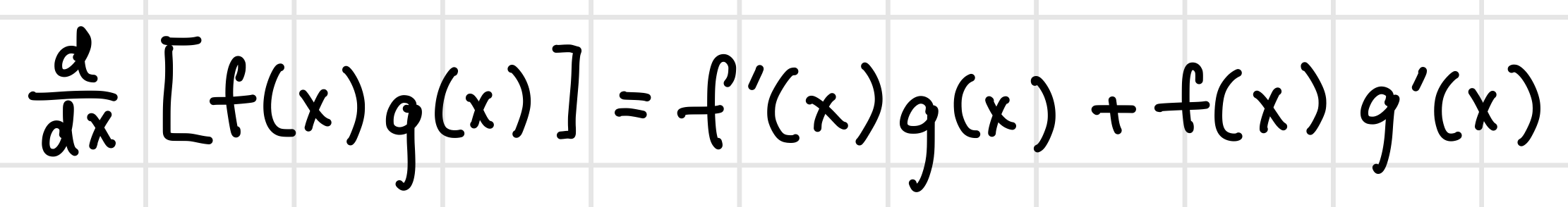
Quotient Rule

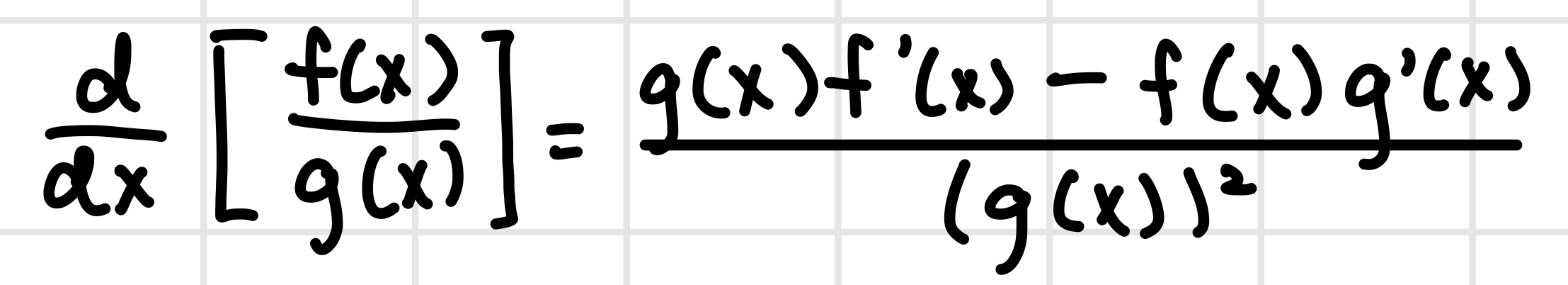
(sinx)’ =

cosx

(cosx)’ =

-sinx

(tanx)’ =

sec² x

(e^x)’ =

e^x

(lnx)’ =

1/x

(a^x)’ =

a^x ln(a)

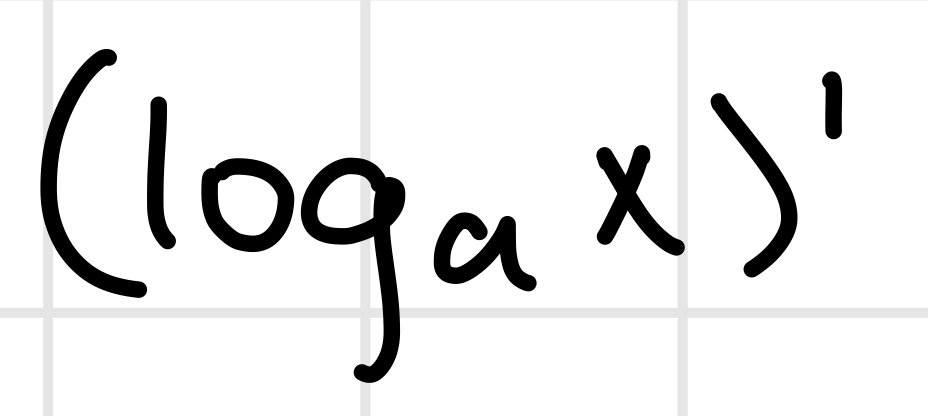
1/(xlna)

Unit 3

Composite, Implicit & Inverse Functions

Chain Rule

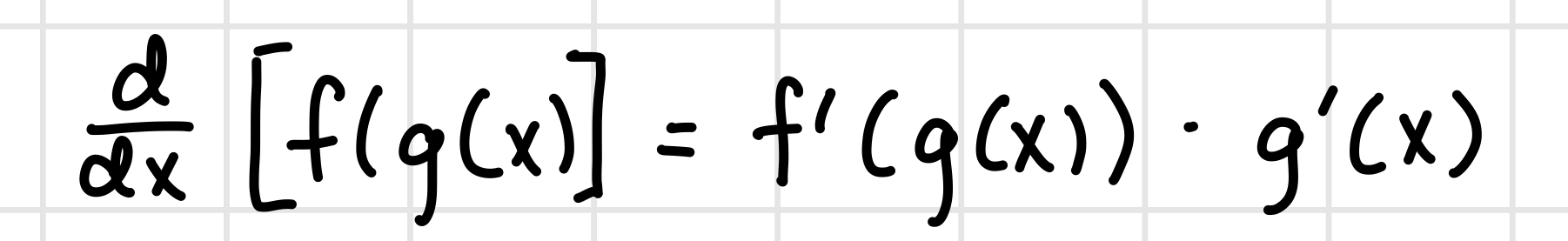
Implicit Differentiation - When x and y are mixed together and you can’t solve for y easily

• Differentiate in terms of x

• When you differentiate a term with y, multiply it by dy/dx

• Collect all the terms involving dy/dx

• Factor and solve for dy/dx

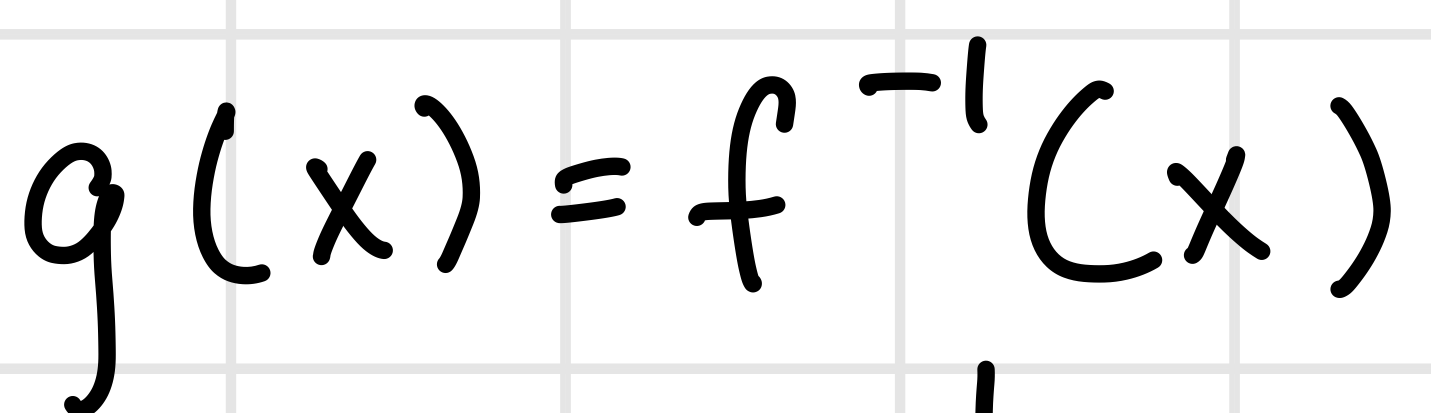
Inverse Functions Derivative

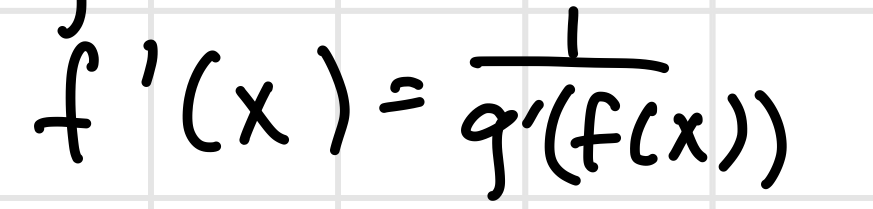
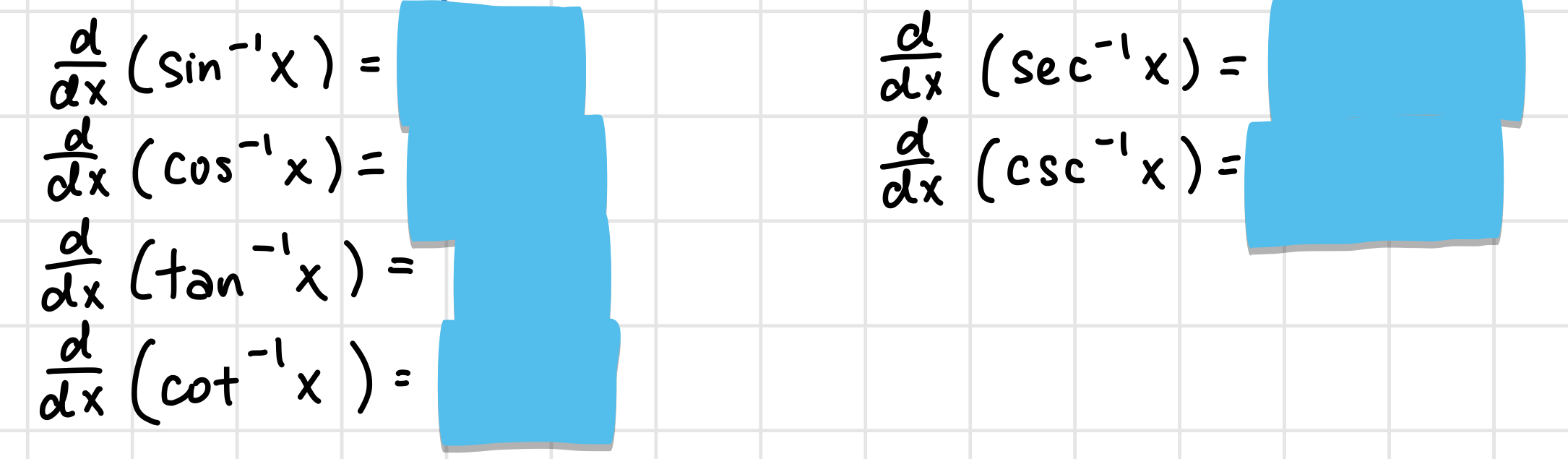
Inverse Trig Functions

Unit 4

Applications of Differentiation

Position, Velocity, Speed & Acceleration

Position = s(t)

Velocity = s’(t)

Speed = |s’(t)|

Acceleration = s’’(t)

Solving for Related Rates

• Identify variables and rates

• Write an equation relating variables

• Differentiate both sides with respect to t

• Plug in known values and solve

Helpful formulas:

Sphere Volume = 4/3pi*r³

Sphere SA = 4pi*r²

Cone Volume = 1/3pi*r²h

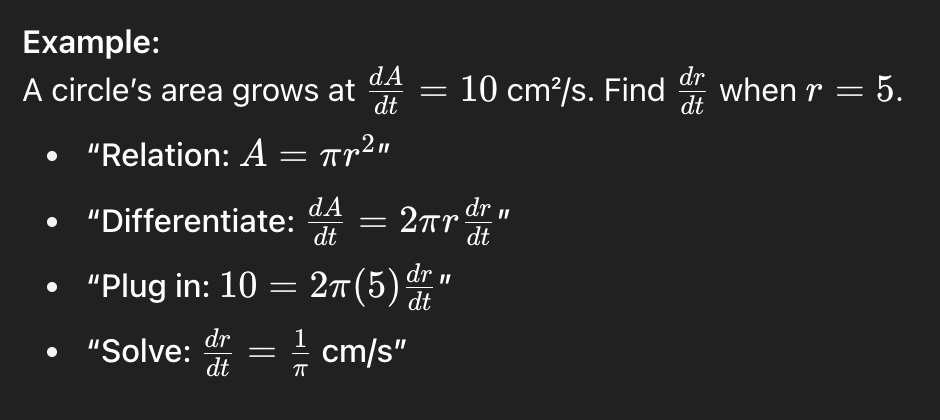
Linear Approximation Equation

The Linear Approximation Equation is used to estimate the value of a function near a given point by using the tangent line at that point x = a

(y-ycoord) = slope (x - xcoord)

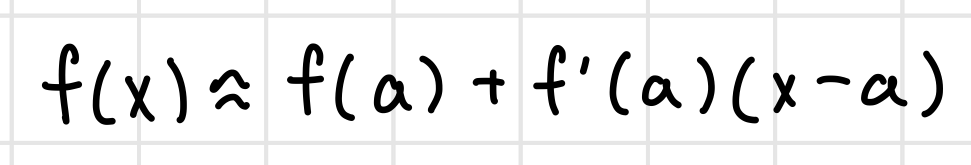
Tangent Line Equation

The Tangent Line Equation is the equation of the line that touches a curve at a given point

y - f(a) = f'(a)(x - a)

where f(a) is the function value at x = a and f'(a) is the derivative at that point.

L’Hospital’s Rule*

Used if limit is in indeterminate form (0/0 or infinity/infinity)

Unit 5

Analytic Application of Derivatives

Mean Value Theorem (MVT)

Usef if f(x) is differentiable on open interval (a,b) and continuous on closed interval [a,b]

There exists at least one point c in (a,b) where the tangent line to the curve is parallel to the secant line connecting the endpoints of the interval (AROC = ROC)

Extreme Value Theorem (EVT)

States that if a function is continuous on a closed interval [a,b], then it has both a maximum and minimum value on that interval.

Local/Relative Extrema - How to tell if its max or min?

if f’(x) changes from positive to negative —> local max

if f’(x) changes from negative to positive —> local min

Absolute Extrema - How to find?

Critical Points

How to determine concavity

Point of Inflection

Unit 6

Integration

Riemann Sum/Approximation

Trapezoid Sum/Approximation*

Definite Integral

Integration Rules**

Fundamental Theorem of Calculus (Part 1)

Fundamental Theorem of Calculus (Part 2)

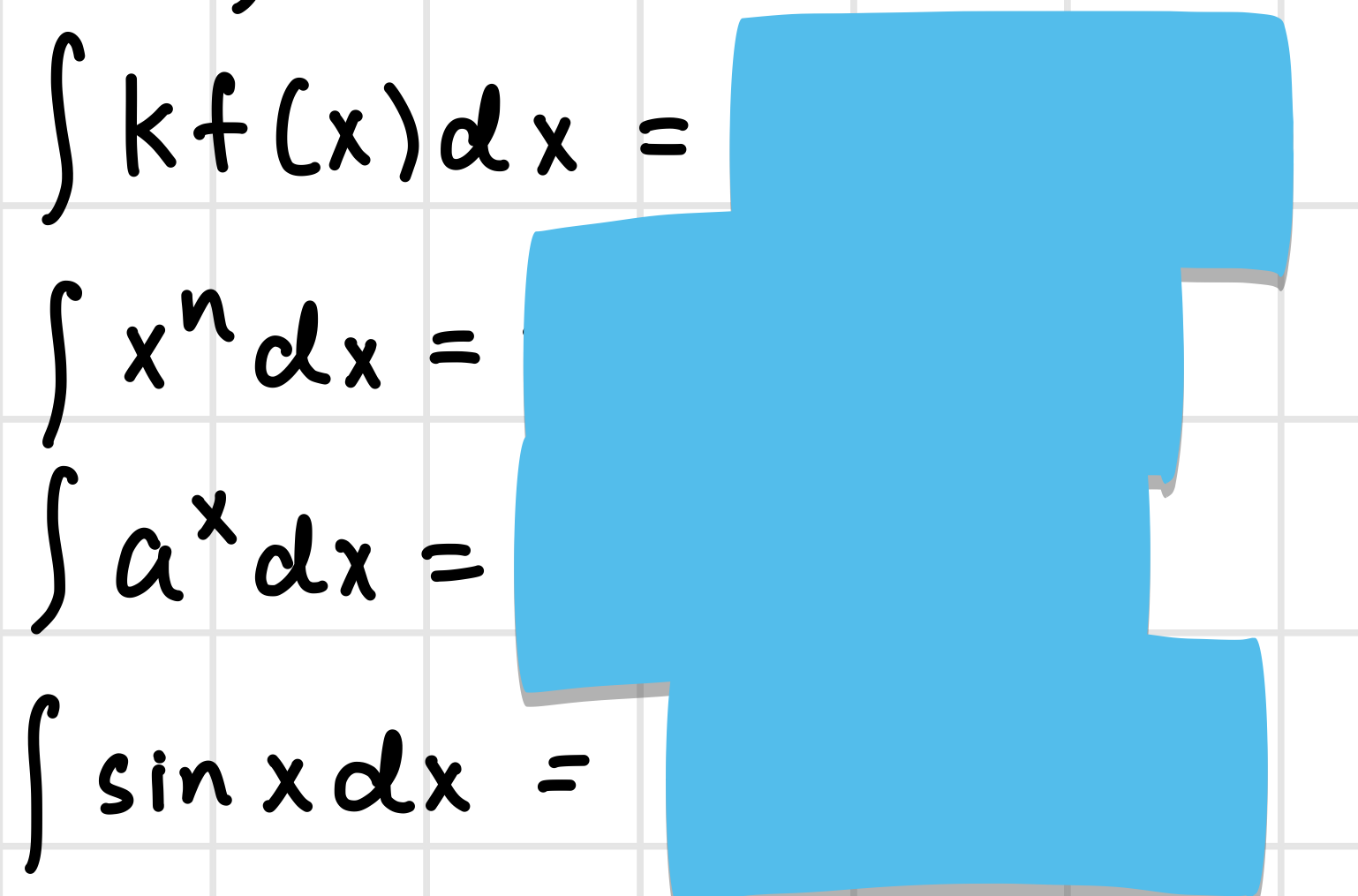
Integration Rules

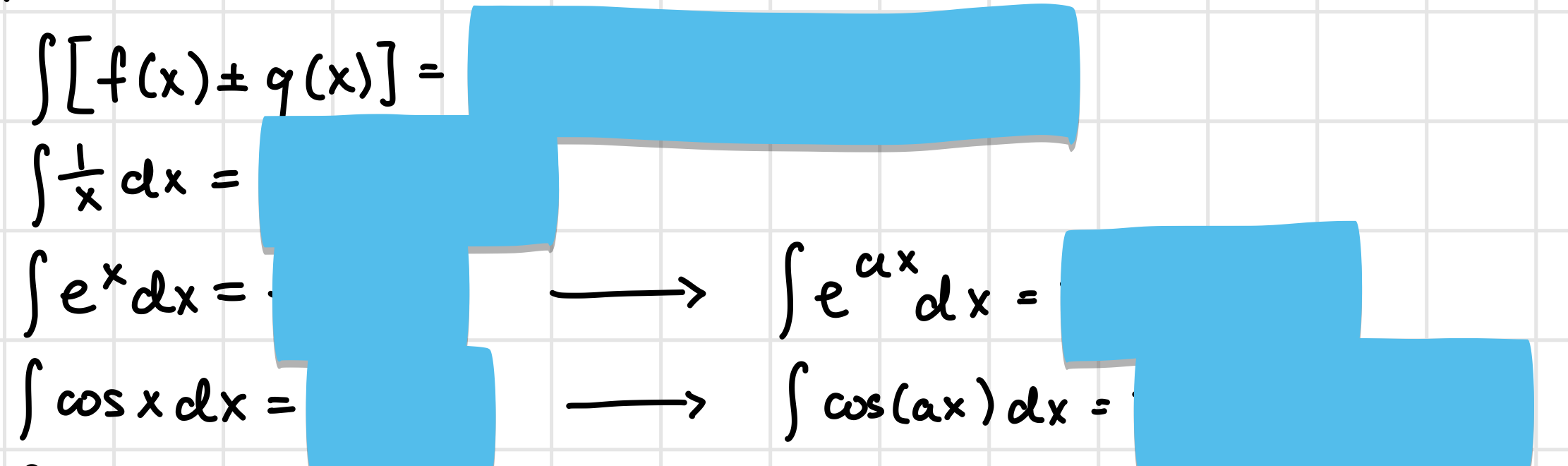
Integration Rules

U-sub*

• Substitute u

• Find du/dx to find dx

• Change bounds to u-values

• Substitude dx into equation and keep u and du

• Integrate and solve normally

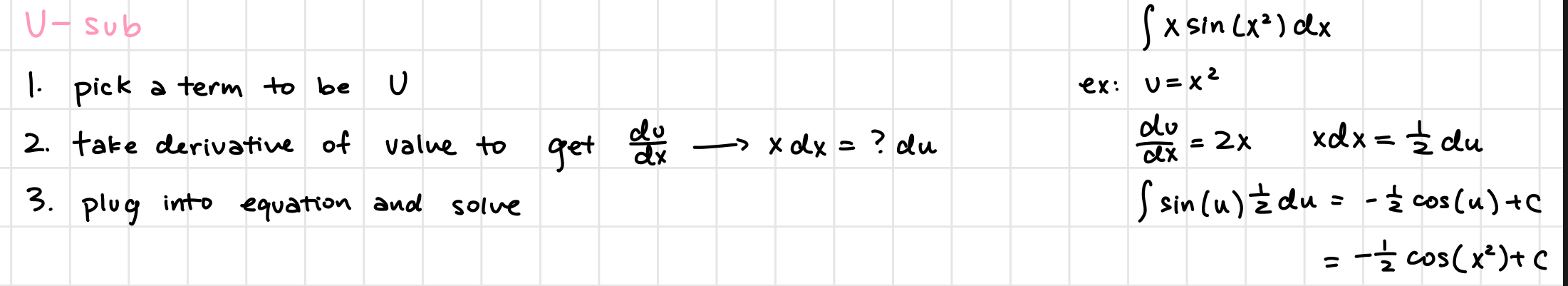
Long Division

Completeing the Square

Linear Partial Fractions*

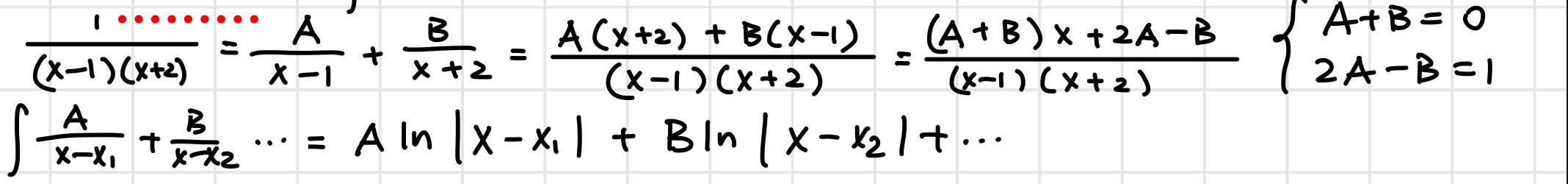
Integration by Parts

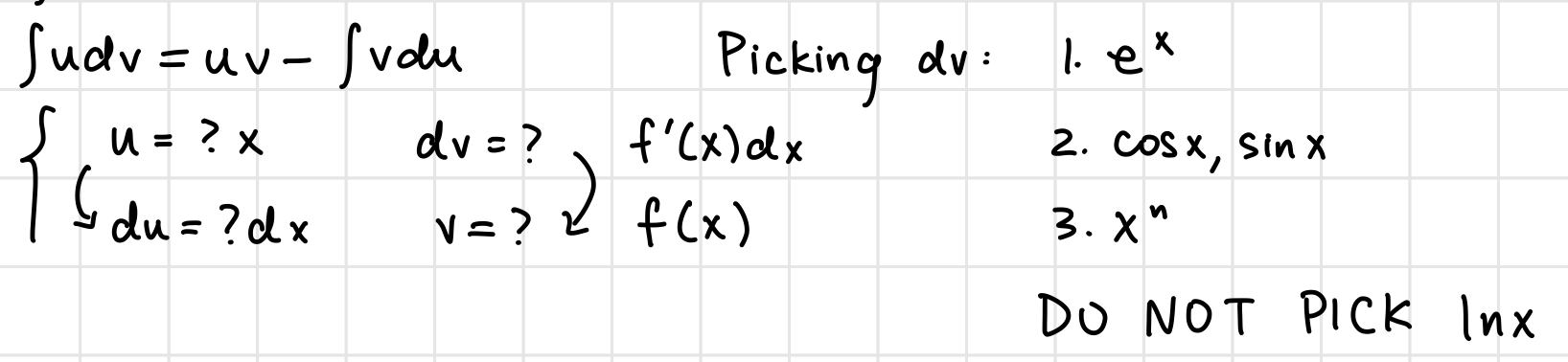
Picking order for Integration by Parts

Improper Integrals - what happens to integral when limit exists vs limit DNE

Unit 7

Differential Equations

Slope Fields

Euler’s Method*

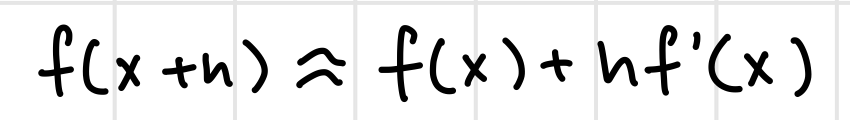
Solving Differential Equations

Exponential Growth/Decay Model: dy/dt = ky

Logistic Growth Model

dP/dt = kP(1-P/L)

represents the rate of change of a population P over time, where k is the growth rate and L is the carrying/environmental capacity.

y = L/2 —> point of inflection/maximum

Unit 8

Applications of Integration

Average Value*

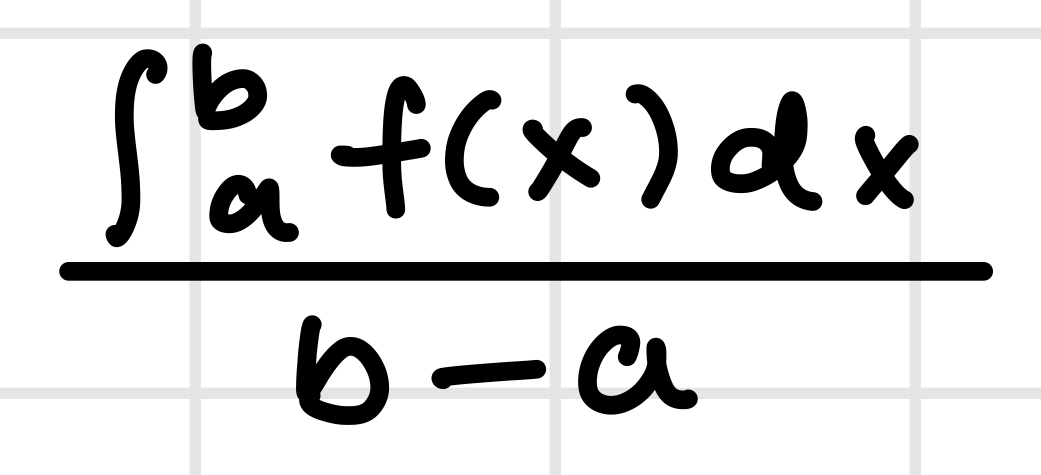
Kinematics: Displacement, Position, and Velocity

Net Change Theorem

Area Between Curves

Finding Volume - Formula

Disk Method (No Hole)

Washer Method (with Hole)

Unit 9

Parametric Equations, Vector Values Functions, Polar Coordinates

Parametric Equation* dy/dx =

(dy/dt) / (dx/dt)

Parametric Equation: dy/dt =

(dy/dx)(dx/dt)

Parametric Equation - 2nd derivative

Speed

Distance

Polar Coordinates: x =, y =

Polar Coordinates: dy/dx =

Area in Polar Coordinates

Area between Polar Curves

Unit 10

Series

How many series tests are there? What are they?

nth Term Test

Geometric Series*

A series where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. The sum can converge to a finite value if the absolute value of the ratio is less than one.

p-series

Harmonic Series

Integral Test

Limit Comparison Test

Direct Comparison Test

Alternating Series Test

Ratio Test*

A convergence test used to determine the absolute convergence of a series by examining the limit of the ratio of successive terms. If the limit is less than one, the series converges; if greater than one, it diverges.

Absolute Convergence

Alternating Series Error Bound

Taylor Series

Maclaurin Series

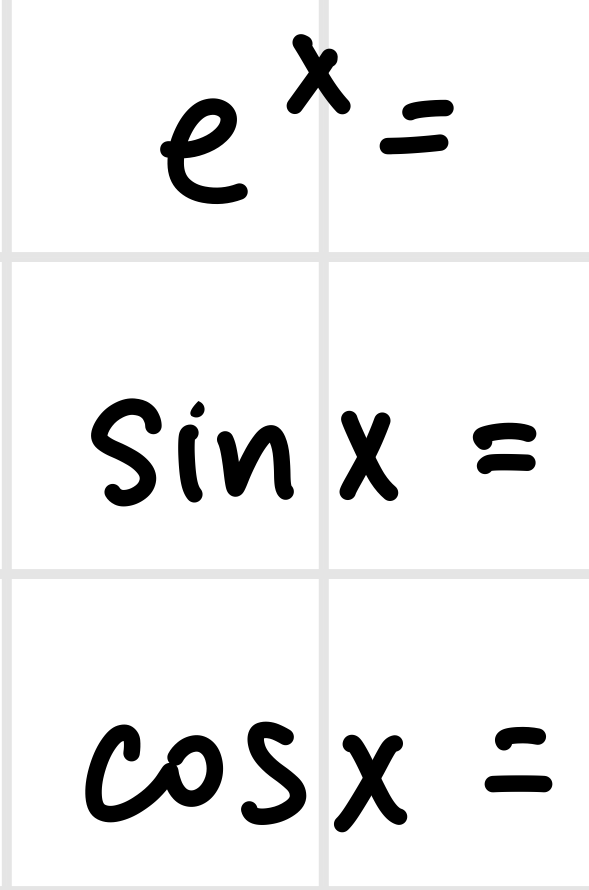
Lagrange Error Bound