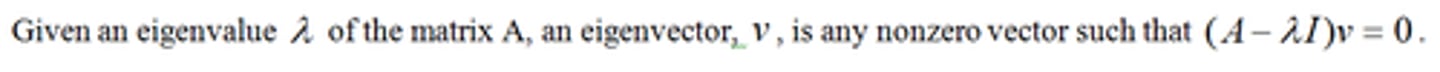Differential Equations Vocabulary

Differential Equation

An equation with derivatives of a function in it.

Linear Operator

An operator L(y) is linear if it satisfies the following conditions:

1. L(y1+y2) = L(y1) + L(y2) where y1 and y2 are functions.

2. L(cy) = cL(y) where c is a constant.

Linear Differential Equation

A differential equation is linear if the operator part of the equation (the part with all of the terms that have dependent variables in them) is a linear operator.

Order

The highest derivative which appears in the differential equation.

Forcing function

All of the terms of the differential equation which do NOT have a dependent variable in them.

Homogeneous

The forcing function is zero, or all of the terms in the differential equation have dependent variables in them.

Nonhomogeneous

The forcing function is not zero.

Exact

A first-order differential equation in differential form: M(x,y)dx + N(x,y)dy = 0 is EXACT if the partial of M with respect to y and the partial of N with respect to x are equal to each other.

Separable

A first-order differential equation is separable if you can write it in the form F(y)dy = G(t)dt.

Constant Coefficients

Only constant multiples of the dependent variable and its derivatives are in the differential equation.

Smooth

A function that has at least one continuous derivative.

Linearly Independent Functions

A set of functions is linearly independent if the only linear combination of the functions that is equal to zero has all of the coefficients equal to zero. That is:

c1y1+c2y2+...+cnyn = 0 only when c1=c2=...=cn=0

Linear Combination of Functions

A linear combination of functions is a sum of multiples of the functions: c1y1+c2y2+...+cnyn

Laplace Transform

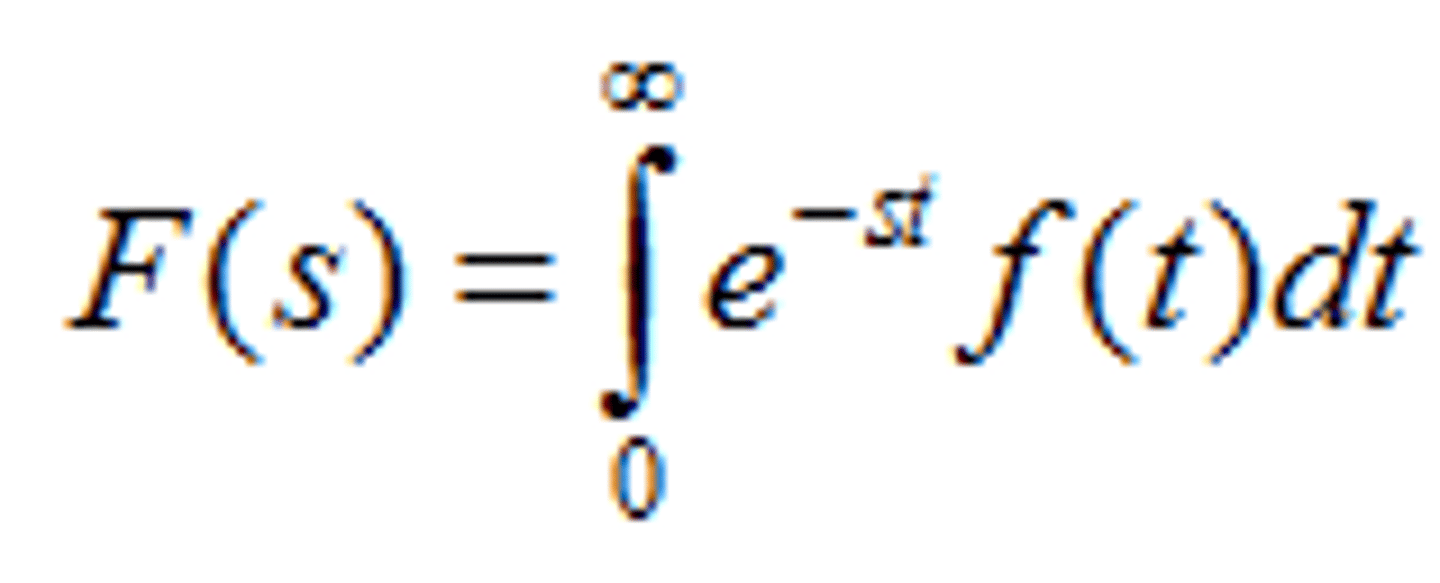
Legendre's Equation

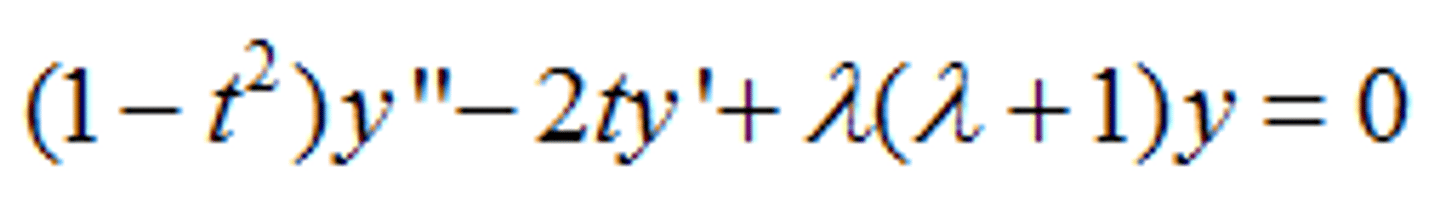
Bessel's Equation

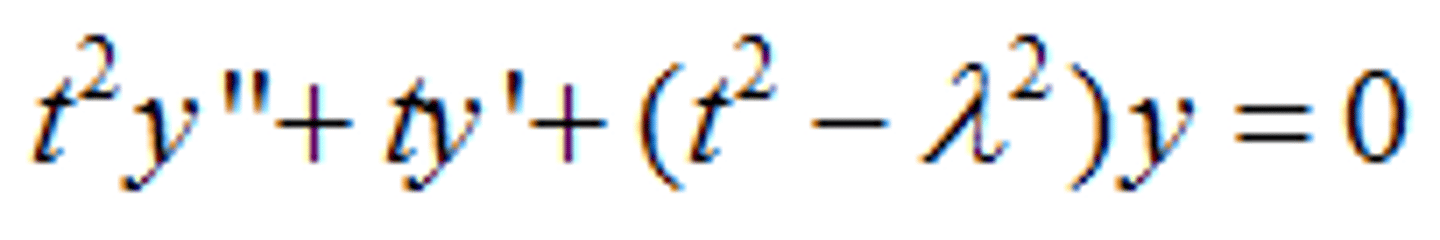
Laguerre's Equation

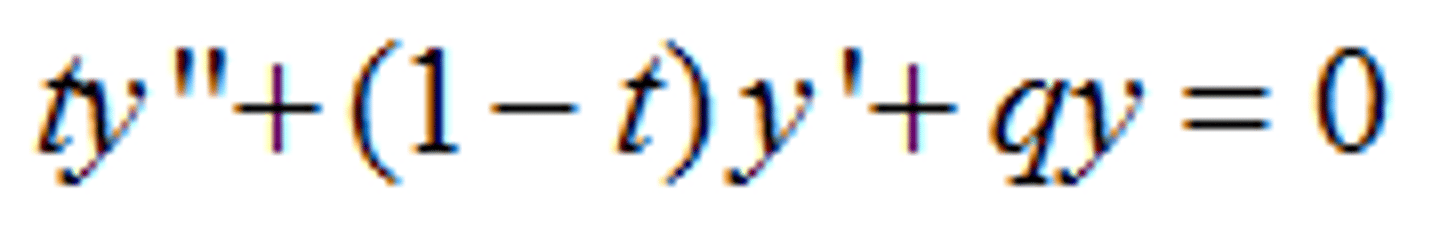
Hermite Equation

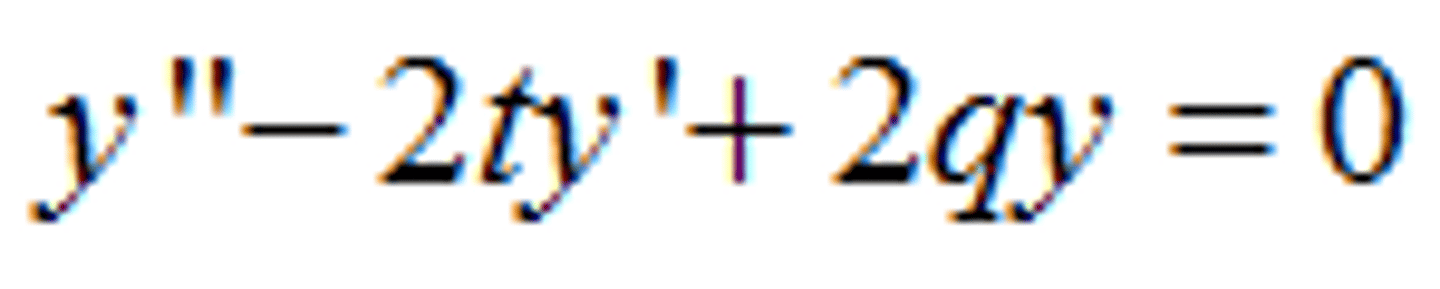
Power Series

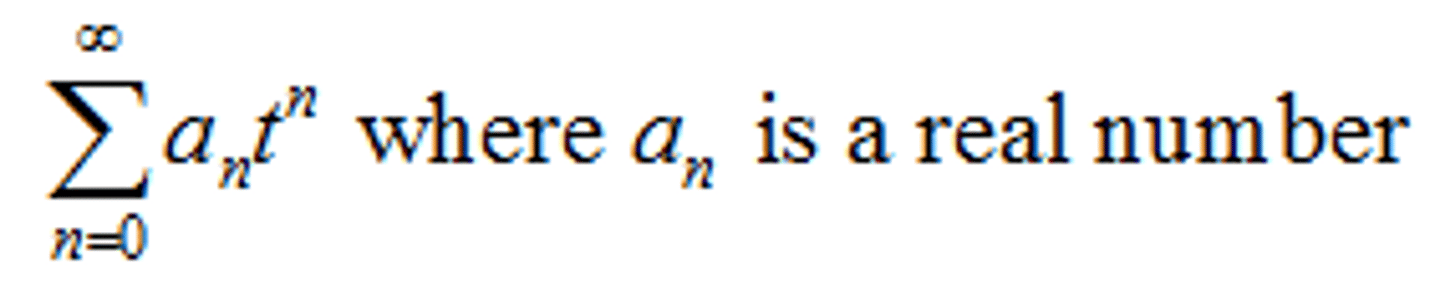
Heaviside (Unit Step) Function

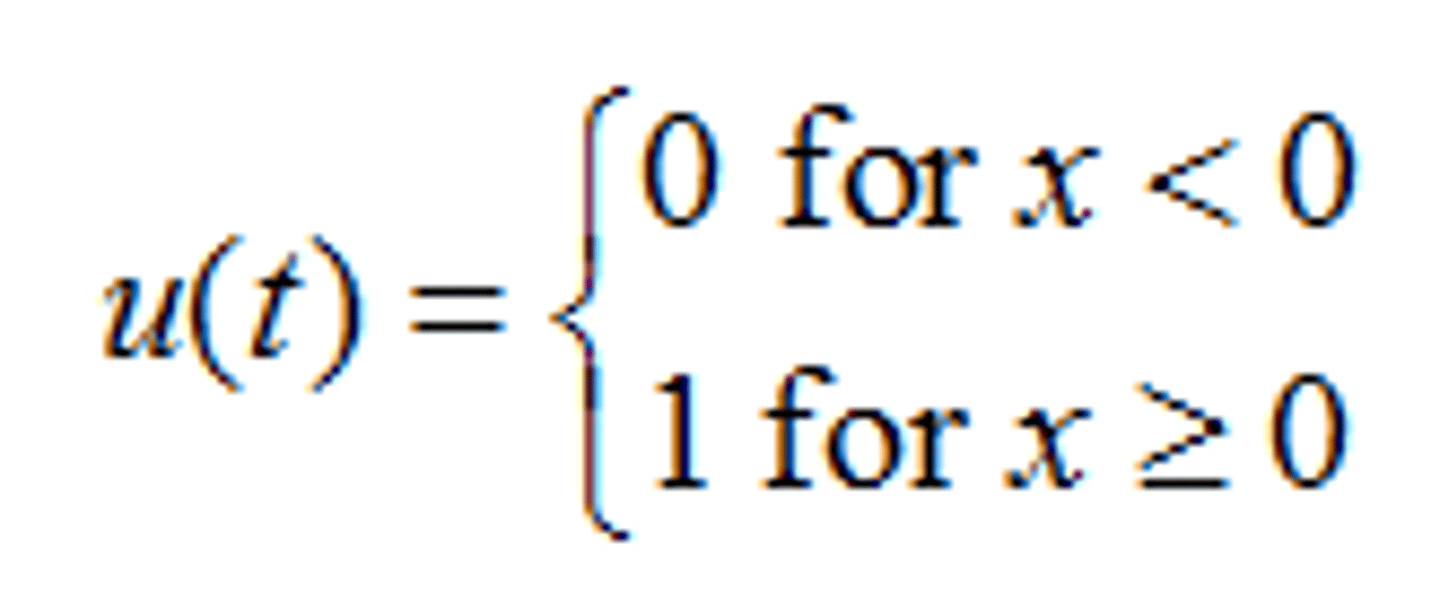
Dirac Delta function

A "function" which, when it multiplies a function inside of an integral, makes the integral equal to the value of the function at the value that makes the input to the delta function zero (see the equation).

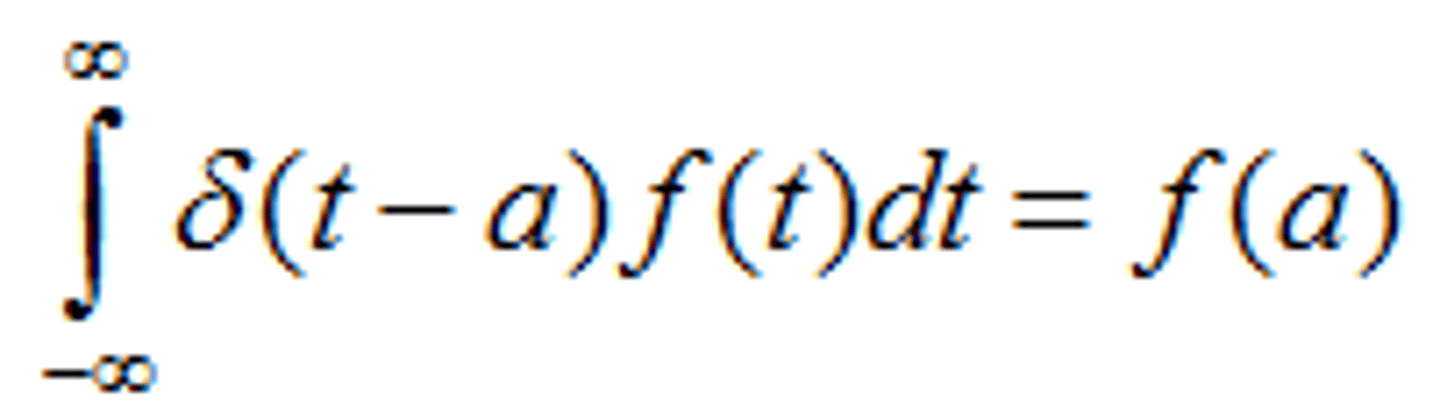
Analytic Function

A function which can be represented as a power series. That is, the function and the power series are equal to each other at all points of the domain of the function.

Ordinary Point

Put a linear differential equation in standard form. A value of the independent variable is an ordinary point, if all of the coefficient functions are analytic.

Singular Point

Put a linear differential equation in standard form. A value of the independent variable is a singular point if at least one of the coefficients is not analytic.

Regular Singular Point

(this definition is for zero being a regular singular point of a second order ODE)

Put a linear 2nd order differential equation in standard form, the zero is a regular singular point if the condition to the left is true.

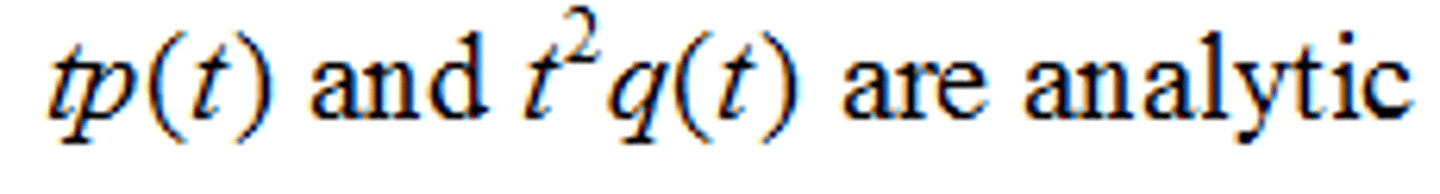
Irregular Singular Point

A value of the independent variable that is a singular point, but not a regular singular point.

Matrix Exponential

Linearly Independent Vectors

Span (of a set of vectors)

All possible linear combinations of the vectors in the set.

Determinant (of a matrix)

Row reduce the matrix to an upper (or lower) triangular matrix using only "multiply and add" operations - no row switching or just multiplication operations. The product of the diagonal elements of the reduced matrix is the determinant of the matrix.

Eigenvalue of a matrix A

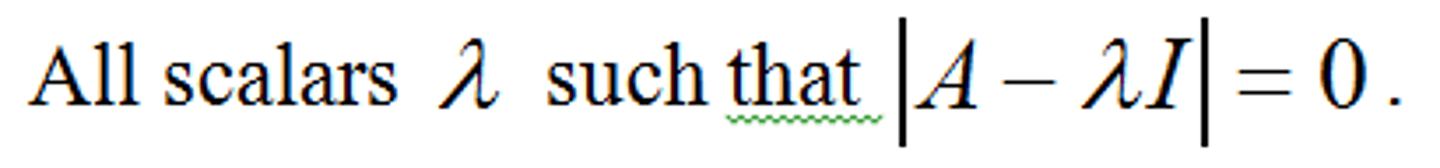
Eigenvector of a matrix A