Null hypothesis testing

The null hypothesis H0 assumes

the sample came from a population where sample mean > population mean (significant difference)

The research hypothesis H1 assumes

the sample came from a population where sample mean = population mean (no significant difference)

Stages of null hypothesis testing

1. formulate hypotheses

2. collect data - sample mean and SDM

3. infer whether the data is inconsistent with H0

4. Fail or fail to reject H0

5. Interpret result in context of hypotheses

When does one fail to reject H0 (not significant)

when p (conditional probability) > a (critical value)

When does one reject H0 in favor of H1 (significant)

when p (conditional probability) < a (critical value)

A result testing H1 - people who buy parrots are more likely to be deaf found that H0 can be rejected.

Infer in context of hypothesis

There is evidence that people who buy parrots are more likely to be deaf

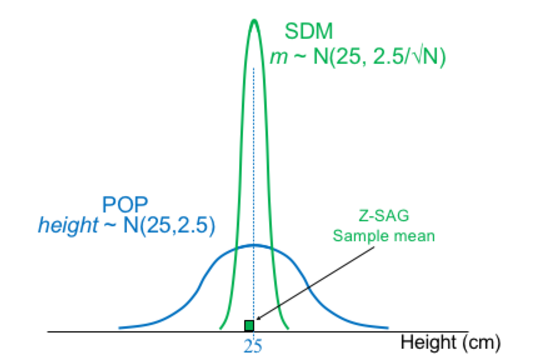
Heights are distributed normally

H1: height of sample is shorter than height of general population

n = 25, sample mean = 24.5

What conclusion can be inferred?

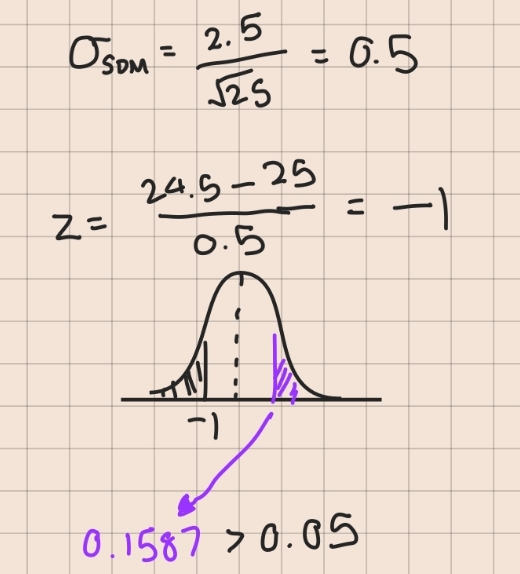
Fail to reject H0 > There is no sufficient evidence that the sample members are significantly shorter than the general population

what is the p value if you use a two tailed hypothesis?

The sum of p on both ends

Rejected H0 but H0 is actually true

Type 1 error

fAiled to reject H0 but H0 is actually false

Type 2 error

How type 1 errors arise

Random errors

How type 2 errors arise

Usually systematic errors

why is a = 5% usually

Not too large (increases risk of type 1 error) or too small (increases risk of type 2 errors)

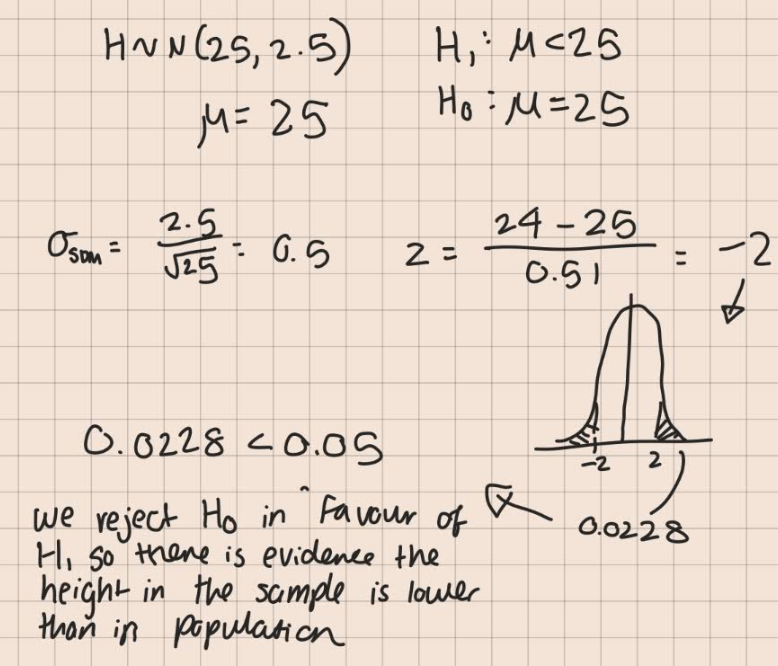
In a population H is distributed normally (25,2.5). In a sample of 25 you predict the mean is less than the population. conduct null hypothesis test at 5% significance

p (0.0228) < 0.05
We reject H0 in favour of H1 so there is evidence the heights of the sample is lower than in the population