kin 216: biomechanics - angular kinematics

what is general motion?

a combination of linear and angular motion

what is linear motion?

• translation

• change in position

• move in the same direction

describing changes in position in space

what is angular motion?

• rotation

• change in orientation

• spin around the same fixed axis

describing rotation in space

when does angular motion occur?

when a body moves along a circular path, revolving around a central line or point

angular motion can also be referred to as…?

rotation

what are the three types of angular movements or rotations?

ypr

• yaw

• pitch

• roll

how many types of linear and angluar movements?

linear: 2; rectilinear and curvilinear

angular: 3; ypr

what is yaw?

rotating to the left or right

what is pitch?

rotating up or down

what is roll?

tilting to the left or right

unlike translation, angular motion keeps a fixed point called… ?

the axis of rotation

what is an external axis of rotation?

• an imaginary line found outside of the body

• system moves in a circular path around the axis (ex. giants around a bar; where the bar is the external axis of rotation)

what is an internal axis of rotation?

• imaginary line found inside of the body

• system moves in a circular path around the axis (ex. hip joint when running/walking; where hip joint is the internal axis of rotation)

what is the standard reference position of the human body called? what does it look like?

the anotomical position

• body is erect

• facing forward

• feet aligned parallel to each other 

• toes forward

• arms hanging straight below shoulders

• fingers extended

• palms facing forward

the anatomical position is used when describing what of the body?

lpm

• locations

• positions

• movements

what is a cardinal planes?

a plane that passes through the midpoint or center of gravity of the body

cardinal planes may be useful for ?

• locating anatomical structures

• describing limb movements

body movements occur as… ?

rotations of the limbs

rotation occur around what and within what?

rotations occur around an axes and within specific planes

what movement is yaw and what axis does it rotate around?

yaw is turn to left or right (ex. saying no)

• to rotate around a longitudinal (vertical) axis

what movement is pitch and what axis does it rotate around?

to look up or down (ex. saying yes)

• to rotate around a mediolateral (a line running from side-to-side) axis

what movement is a roll and what axis does it rotate around?

tilting the head to the left or right shoulder

• rotating around an anterioposterior axis

the direction of the axis of rotation is found perpendicular to

the plane of motion

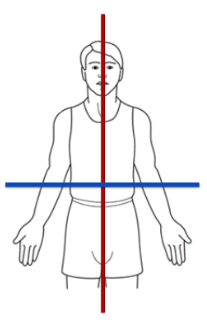
what plane corresponds with the longitudinal axis? and what movements would occur in this plane?

• the transverse (horizontal) plane

• medial/lateral rotation, YAW

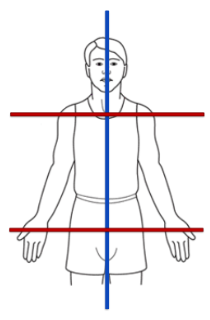
what plane corresponds with the mediolateral axis? and what movements occur in this plane?

• the sagittal plane

• flexion/extension, hyperextension, PITCH

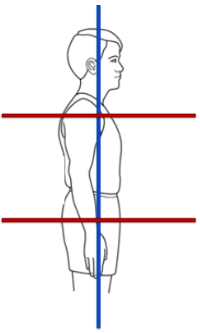
what plane corresponds to the anterioposterior axis? and what movements would occur in this plane?

• the frontal plane

• abduction/adduction, elevation/depression, lateral flexion, ROLL

what is the instant centre?

where the movement is coming from

what information do we first require when measuring angular movement?

• identify the location of three joint centers of rotation (instant center)

• identify the orientation of the two logitudinal segments

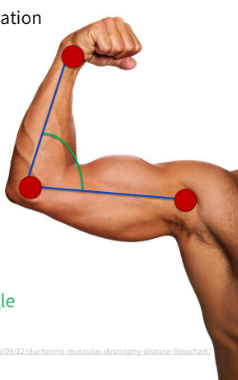
3 joint centers and 2 longitudinal segments will identify what?

1 joint angle

what is a relative angle?

the space between the longitudinal axes of adjacent segments. can be:

• internal

• external

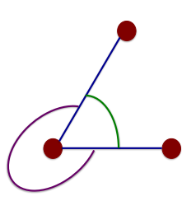
what is the internal angle

the angle formed inside the joint

what is the external angle

the angle formed on the exterior surface of the joint

what is an absolute angle?

the space between a body segment with respect to a fixed line of reference

• can be between the longitudinal segment and EITHER the x- or y- axes

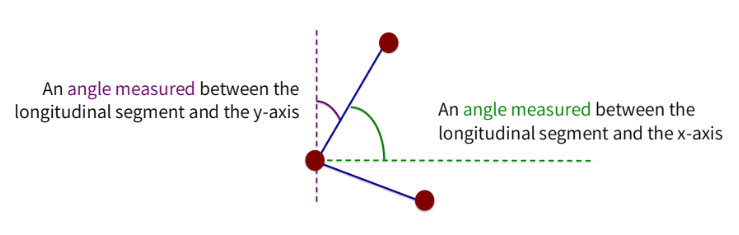
what is a degree?

a common method for measuring angles

• arbituary unit of measurment

• useful to ancient astronomers

• once around the circle is 0degrees to 360degrees

what is a revolution?

simple and natural measurment

• once around the circle

• 1 full turn

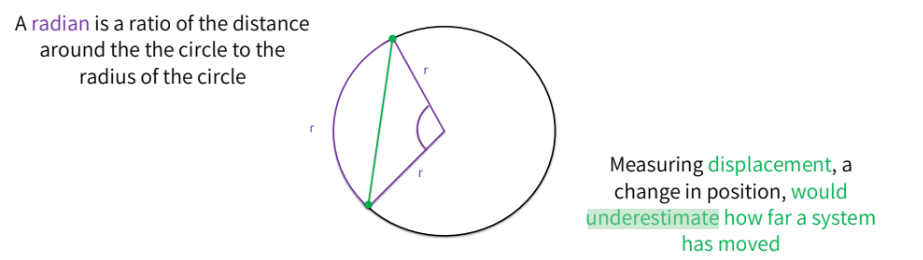
what is a radian?

equal to 57.3degrees

• invented in the 1700s by mathematicians who wanted to define angles rationally 

• a ratio between the angle in a circle and the length of the arc

• where the arc length is equal to the radius

what do radians take into account?

take Pi into account

Pi = 3.14

which of the following is the standard unit of measure for angular variables when measuring human movement?

a) degrees

b) radians

c) revolutions

d) all of the above

all of the above (degrees, radians, and revolutions) are acceptable units of measure

360 degrees is equal to how many revolutions?

1 revolution

1 revolution is equal to how many radians?

2Pi rad

2Pi rad is equal to how many degrees?

360 degrees

how many degrees is in one rad?

57.3 degrees

what is a goniometer? in what profession is it widely used and why?

an instrument that measures an angle

• widely used in physical therapy to assess range of motion before and after intervention (tracking progress over time)

(gonia-angle) (metron-measure)

what is a basic goniometer useful for?

• static analysis

• angles in pictures

what is an electrogoniometer useful for?

• dynamic analysis

• taking measurements during movement

what is different about measuring body angles when compared to angles such as a moving door, for example?

• a door rotates in a fixed position around a hinge; the axis of rotation is usually in a fixed position

• in the body, the axis of rotation at a joint is not fixed; the longitudinal segment shifts position because the axis migrates

how can you be certain of the precise location of the origine of movement  (instant center)?

you cant! haha

• when analyzing human movements, we estimate the position of the axis of rotation

what is angular distance?

phi

the total amount of rotation - scalar quantity

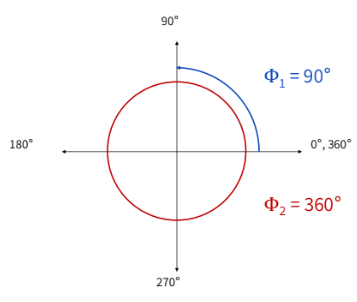
what is angular displacement?

theta

the change in angular position - vector quantity

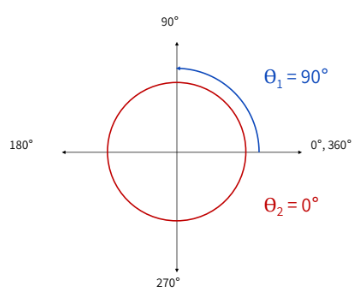
what do we use to describe the objects position in space?

• phi - angular distance (scalar)

• theta - angular displacement (vector)

what do we use to decribe the temporal patterns of movement?

• sigma - angular speed (scalar)

• omega - angular velocity (vector)

what is angular speed?

sigma

change in angular distance (phi) over a change in time - scalar quantity

what is angular velocity

omega

change in angular displacement (theta) over a change in time - vector quantity

what is dynamic motion characterized by?

dynamic motion is characterized by a change in angular velocity

what producs a change in angular velocity?

torque

what is angular acceleration

alpha

change in angular velocity (omega) over a change in time

what do the signs in front of the displacement and velocity values tell us about human movement?

• positive values mean that the system is rotating counter-clockwise

• negative values tell us that the system is rotating clockwise

what does the sign in front of acceleration value mean?

you dont know! because it could either be:

• the direction

OR

• weather the system is speeding up or slowing down

further detail (context) is necessary to answer this question

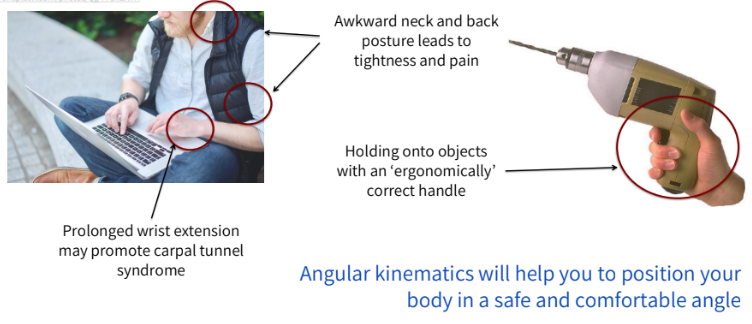
angular kinematics in the everyday can helps with what?

angular kinematics will help you position your body in a safe and comfortable angle

• can help decrease risk for carpal tunnel

most examples of human movement are: 

general motion (both)

• we could analyze the rotation at the joints 

• we could analyze the translation of the limbs

what is the relationship between the two forms of motion (rotation and translation)?

• the more the ball spins the further the ball travels

• the faster the ball rotates the faster the ball translates

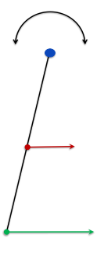
if this line segment was to represent ur arm, what part is the axis of rotation? and what part is translating?

• the blue part would be the axis of rotation (the origin of motion) at your shoulder

• the red and green parts would represent your elbow and hand respectively. as the arm swings back and forth, they each change position (or translate)

the linear change in position on a rotating object will be different where? what is this dependant on?

at EACH point along the system

• the amount of change is dependant upon the radius of rotation

what is the radius of rotation (r)?

the distance between the axis of rotation and the point of interest on a system

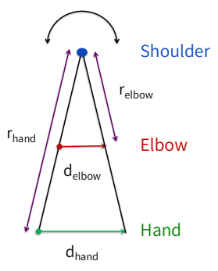
what equation is used for determining how far a point on that system translates when a system rotates about an axis?

length = radius of rotation x angular distance (phi)

what equation is used for determining how fast a point on a system translates when a system rotates about an axis?

velocity = radius of rotation x angular velocity

what equation is used for determining the size of the dynamic change when a system rotates about an axis?

acceleration = radius of rotation x angular speed

why do we use linear and distance (scalar quantities) and also velocity and acceleration (vector quantities)?

measuring displacement, a change in position, would underestimate how far a system has moved

• in order to account for angular movement, we take into account the total amount of linear movement (distance), not the displacement

• a radian is the ratio of the distance around the circle to the radius of the circle

why does a batter “choke up” (slide their hands away from the handle)?

if distance is not a factor — and the athlete just wants to ensure they make contact with the ball, players will often grab up on the bat to improve accuracy by decreasing the radius of rotation; as velocity decreases, accuracy increases

why does a batter “choke down” (slide their hands as low on the bat as possible)?

in order to hit as far as possible (1/2mv²) - as fast as they can, they grab on to the end of the bat to increase the radius of rotation so that velocity is increased.

the direction of the linear movement is _______ to the rotating object

tangent.

• if the ball spins in a clockwise direction the ball would translate to the right” etc.

tangentional

reminds you that there was an angular movement that gave rise to a linear change

both formulas for tangentional velocity and linear velocity do what? why

solve for linear velocity

• tangentional velocity takes into acount angular velocity which is important when discussing centripital motion: if an object is moving around a curve at a constant speed, even though its magnitude of velocity isn’t changing, its direction (sign) changes through the different points; i.e. if velocity is changing then acceleration is present (even though its moving with a constant speed)

a point on an opject spinning at a constant velocity is constantly changing _____ and is experiencing ______________.

direction, linear acceleration (centripital acceleration)

centripital (or radial) acceleration is present when…?

when an object changes direction

where is the force that causes centripetal acceleration to occur directed?

it is directed towards the axis of rotation, this force causes a change in direction

ar = v²/r

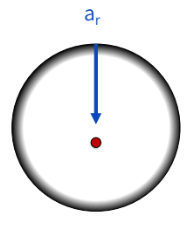
what is centripital acceleration?

the linear acceleration directed towards the axis of rotation

ar = v²/r

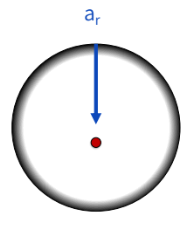
what is the relationship between the radius of rotation, force, and turn velocity

ar = v²/r

• ar increases as radius of rotation decreases; more force would be required to make a sharper turn

• ar increases as velocity increases; more force would be required to make a faster turn

as the sharpness of turn increases, the velocity must decrease

when competing a 400 meter race, is there one lane that offers a biomechanical advantage?

the outside because, with a larger radius of rotation, velocity increases

what is the total acceleration of a system?

the vector sum of the tangentional acceleration and the centripetal acceleration

what is the relationship between the lengths of golf clubs and the distance they can hit

the longest club is the driver and the shortest club is the pitching wedge

• even with the same movement input, drivers hit the ball farther than the pitching wedge

what is the importance of stretching our joints before exercise? 

• stretching increases range of motion at a joint.

a greater rage-of-motion (angular displacement; linear displacement is related to the amount of angular rotation) will affect both linear and angular changes — leading to improved performance

there is a non-linear relationship between which linear and angular variables when it comes to what?

internal movements; movements inside the human body

• linear changes occur at the muscle

• Angular changes occur at the joint

THERE IS A NONLINEAR RELATIONSHIP BETWEEN VELOCITY AND ANGULAR VELOCITY