Research Methods Midterm

experiment

any process producing an outcome

outcome

the result of a trial

event

a specific outcome or set of outcomes

sample space (S)

all possible outcomes

mutually exclusive

events that cannot occur together (e.g., dead/alive)

independent events

one event does not affect the other

complement

the opposite of an event (A and A’)

P(A)

Probability of event A occurring (e.g., rolling a 4 on a die).

P(A′)

Probability of A not happening (the complement).

Complement rule

The probability that an event does not occur = 1 minus the probability it does occur.

[ P(A’) = 1 - P(A) ] 

A∪B (“A or B”)

The union of A and B — means A happens, or B happens, or both happen.

Mutually Exclusive Events

Two events that cannot occur together.

P(A and B) = 0

Independent Events

Two events where the outcome of one does not affect the other.

P (A and B) = P(A) x P(B)

Dependent Events

Two events where the outcome of one changes the probability of the other.

Conditional Probability

Probability of A occurring given that B has already happened.

P(A∣B)= P(A and B) / P(B)

Law of Addition (General Form)

Used for “A or B”

P(A or B) = P(A) + P(B) − P(A and B)

Law of Addition (Mutually Exclusive)

If A and B can’t happen together:

P(A or B) = P(A) + P(B)

Law of Multiplication (Independent Events)

Used for “A and B.”

P(A and B) = P(A) × P(B)

Law of Multiplication (Dependent Events)

When one event affects the other.
P(A and B) = P(A∣B) × P(B)

“Or” in probability

Means union (either event or both). Symbol: ∪

“And” in probability

Means intersection (both events occur). Symbol: ∩

P(A∣B) (“Given that”)

Means one event has already happened. Used in conditional probability

Probability Range

All probabilities fall between 0 and 1.

0 ≤ P(E) ≤ 1

Sum Rule of Complements

An event and its complement together always equal 1.

P(A) + P(A’) = 1

random variable

a variable whose possible values are outcomes of a random process (e.g., number of sick patients)

discrete random variable

a variable that takes countable values (whole numbers only)

(ex: number of hospital visits, number of smokers)

continuous random variable

a variable that takes any value in a range (including decimals)

(ex: height, weight, blood pressure)

probability distribution

a function that shows all possible outcomes and their probabilities

discrete probability distribution

probability distribution for a discrete random variable (counted data)

(ex: bionomial, poisson)

continuous probability distribution

probability distribution for a continuous variable (measured data)

(ex: normal, exponential, gamma)

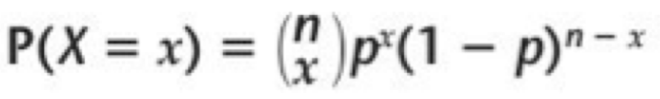
bionomial distribution

A discrete distribution showing the probability of a given number of “successes” in n independent trials.

Requirements for Binomial Distribution

• Fixed number of trials (n)

• Two outcomes per trial (success/failure)

• Independent trials

• Constant probability of success (p)

n (in Binomial formula)

number of trials

x (in Binomial formula)

number of successes

p (in Binomial formula)

the probability of success on each trial

(1−p) (in Binomial formula)

the probability of failure on each trial

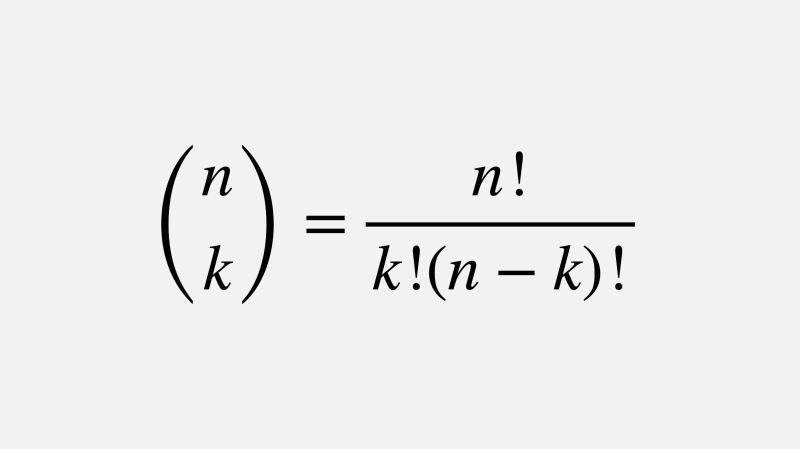
(n choose k) (usually denoted as (n choose x)

Number of ways to choose x successes from n trials.

Factorial (!)

Product of all positive integers up to that number.

4!=4×3×2×1=24

Complement in Binomial Problems

Sometimes easier to find the opposite event and subtract from 1.

ex: “At least one” = 1−P(X=0)1 - P(X=0) 1−P (X=0)

Normal Distribution

Continuous, bell-shaped distribution that’s symmetric around the mean.

Mean (μ) of Normal Distribution

The center of the distribution; where the curve is highest.

Standard Deviation (σ) of Normal Distribution

Measures spread; how far data fall from the mean.

Properties of Normal Distribution

• Bell-shaped and symmetric

• Mean = median = mode

• Total area under curve = 1

Empirical Rule (68–95–99.7 Rule)

• 68% of values fall within 1σ of mean

• 95% fall within 2σ

• 99.7% fall within 3σ

Standard Normal Distribution

A normal distribution with mean = 0 and standard deviation = 1.

Z∼N(0,1)

Z-Score

Measures how many standard deviations a value is from the mean.

Z = X - μ​ / σ

Z-Table

A table that gives the probability (area) under the standard normal curve up to a given Z-score.

P(Z < a)

Probability that Z is less than a given value (area to the left of a on a curve.

P(Z>a)

1 minus the probability to the left.

P(Z > a) = 1 − P (Z < a)

P(a<Z<b)

Area between two Z-scores.

P(Z < b) − P(Z < a)

Area Under the Normal Curve

Represents probability; total area = 1 (or 100%).

Shape of Normal Curve

Bell-shaped, symmetric, and unimodal (one peak).

Example of Normal Variable

Height, weight, blood pressure, or test scores.

Hypothesis Testing

A statistical method for making decisions about population parameters based on sample data.

Statistical Hypothesis

A statement about a population parameter that can be tested using sample data.

Null Hypothesis (H₀)

The statement that is there is no effect, no difference or no relationship in the population

Alternative Hypothesis (H₁ or H_a)

The statement that there is an effect, difference, or relationship in the population.

Example of a Null Hypothesis

There is no significant difference in blood pressure between men and women.

Example of an Alternative Hypothesis

There is a significant difference in blood pressure between men and women.

Type I Error (α)

Rejecting H₀ when it is actually true (a false positive)

ex: saying a treatment works when it doesn’t

Type II Error (β)

Failing to reject H₀ when it is false (a false negative)

ex: saying a treatment doesn’t work when it actually does

Power of a Test

The probability of correctly rejecting a false null hypothesis

Power = 1 - β

Significance Level (α alpha)

The threshold for deciding when to reject H₀.

Common values are 0.05 or 0.01

P-value

The probability of obtaining results as extreme as (or more extreme than) your sample, assuming H₀ is true

Decision Rule for Hypothesis Testing

If p < α: Reject H₀

If p > α: Fail to reject H₀

Interpretation of Small P-value

The data provide strong evidence against H_0; an effect likely exists

Interpretation of Large P-value

There is not enough evidence to reject H₀

Level of Significance vs P-Value

α is chosen before the test; the p-value is calculated after data collection to compare against α.

Step 1 of Hypothesis Testing

State the null and alternative hypotheses

Step 2 of Hypothesis Testing

Choose the significance level (α alpha)

Step 3 of Hypothesis Testing

Collect data and calculate the test statistic

Step 4 of Hypothesis Testing

Find the p-value using tables or software

Step 5 of Hypothesis Testing

Compare p-value to α (alpha) and make a decision (reject or fail to reject H₀)

Step 6 of Hypothesis Testing

Draw a conclusion and interpret results in context

One-sided (One-tailed) Test

Tests for a difference in one direction only (e.g., “greater than” or “less than”).

Two-Sided (Two-tailed) Test

Tests for a difference in either direction (e.g., “not equal to”).

Statistical Inference

Using sample data to make general conclusions about a population

Example of a statistical decision

“At α = 0.05, since p = 0.02 < 0.05, we reject the null hypothesis.”

Common Mistake in Interpretation

Saying “we accept H₀.” Instead, say “we fail to reject H₀​.”

Classical Probability

Based on equally likely outcomes (e.g., fair dice)

Empirical Probability

Based on observed data or repeated trials

Subjective Probability

Based on personal judgement or belief

Upper-tail test

Tests if the sample mean is greater than the hypothesized mean

Lower-tail test

Tests if the sample mean is less than the hypothesized mean

Two-tail test

Tests if the sample mean is simply different (either direction)

Example of Hypothesis Pair

H₀: No difference between males and females in mean BP

H₁: There is a difference between males and females in mean BP

Two diseases can occur in a patient independently of each other. What probability rule should you use to find the chance that both occur?

Law of Multiplication for independent events → P(A and B) = P(A) × P(B)

A patient is either “HIV positive” or “HIV negative.” What kind of events are these?

Mutually exclusive — they cannot occur together, so P(A and B) = 0

If 20% of the population smokes, what is the probability that someone selected does not smoke?

Complement rule → 1 − 0.20 = 0.80

You roll a die. A = “roll even,” B = “roll greater than 3.” What outcomes belong to “A or B”?

{2, 4, 5, 6} → includes all in A, all in B, and the overlap (4, 6)

A coin is flipped twice. What is the probability of getting two heads?

Independent events → 0.5 × 0.5 = 0.25

What probability concept do you use when a question says “Given that”?

Conditional probability → P(A∣B) = P(A and B) / P(B)

In a survey, 60% like tea, 40% like coffee, and 20% like both. What’s the probability someone likes tea or coffee?

P(A or B )= 0.6 + 0.4 − 0.2 = 0.8

A public health researcher wants to know the chance that a lab test correctly detects disease given the person is infected. What probability type is this?

Conditional probability — the condition “given infected” affects the probability.

If you toss a fair coin 10 times, what type of probability distribution applies to the number of heads?

Binomial distribution (discrete outcomes: success or failure)

What is the probability of getting 0 heads in 10 flips of a fair coin?

P (X = 0) = (10 choose x) (0.5)⁰ (0.5)¹⁰ = 0.00098

A student’s test score has μ = 80 and σ = 10. What is the z-score for a score of 90?

Z=(90−80)/10=1

What proportion of data in a normal distribution lies within 2 standard deviations of the mean?

About 95% (empirical rule)

If a z-score is 1.25, what does that mean?

The value is 1.25 standard deviations above the mean.

A researcher finds P(Z < 1.42) = 0.9222 and P(Z < 1.25) = 0.8944. What is P(1.25 < Z < 1.42)?

0.9222 - 0.8944 = 0.0278