Section 6.3: Centripetal Force

Centripetal acceleration

a_c = v²/r

Centripetal acceleration with angular velocity

a_c = rw²

Magnitude of centripetal force

F_c = ma_c

Centripetal force

Any net force causing uniform circular motion

Two expressions for the centripetal force F_c in terms of mass, velocity, angular velocity, and radius of curvature:

1. F_c = (m* v²)/F_c

2. F_c = mrw²

Finding r for Centripetal force

r = mv²/F_c

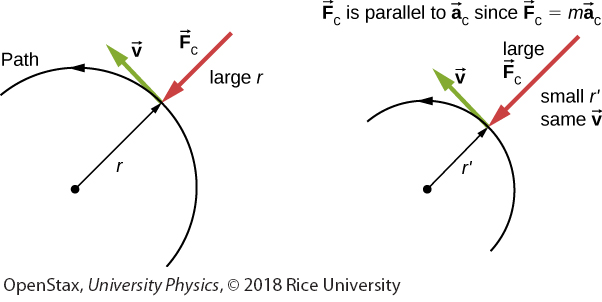
The frictional force supplies the centripetal force and is numerically equal to it. Centripetal force is perpendicular to velocity and causes uniform circular motion. The larger the F_c,t he smaller the radius of curvature r and the sharper the curve. The second curve has the same v, but a larger F_c produces a smaller r’.

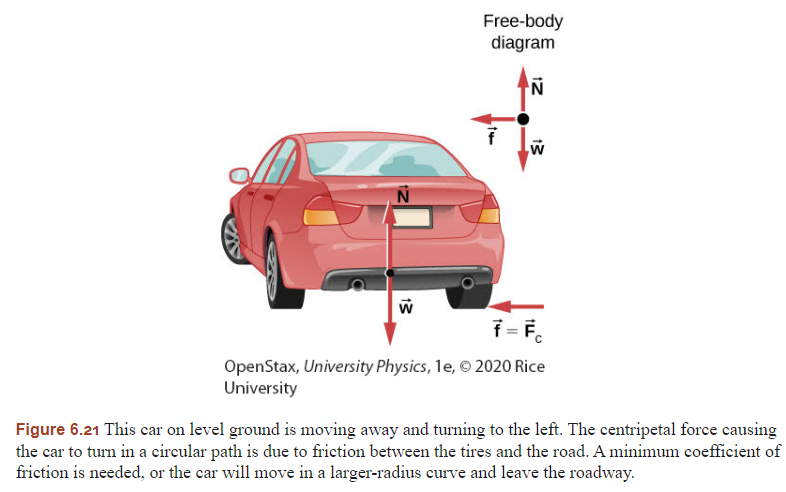
What is the formula for centripetal force needed for a car to negotiate a flat curve, and how does it relate to the coefficient of friction?

The formula for centripetal force is Fc = mv²/r, where:

• m = mass of the car

• v = velocity

• r = radius of the curve For a car to successfully navigate the curve, the friction force must provide this centripetal force. The relationship between friction and centripetal force is: μs = v²/(rg) where μs is the coefficient of static friction and g is acceleration due to gravity.

A car is traveling 18.0 m/s on a flat country road with a curve radius of 100 m. What must be the minimum coefficient of static friction to keep the car from slipping?

To solve this:

1. Use the formula μs = v²/(rg)

2. Plug in the values:

   • v = 18.0 m/s

   • r = 100 m

   • g = 9.80 m/s²

3. Calculate: μs = (18.0 m/s)²/(100 m × 9.80 m/s²) μs = 324/(980) ≈ 0.33 The minimum coefficient of static friction needed is 0.33 to prevent slipping.

Banked curves

Curve in the road that is sloping in a manner that helps a vehicle negotiate the curve.

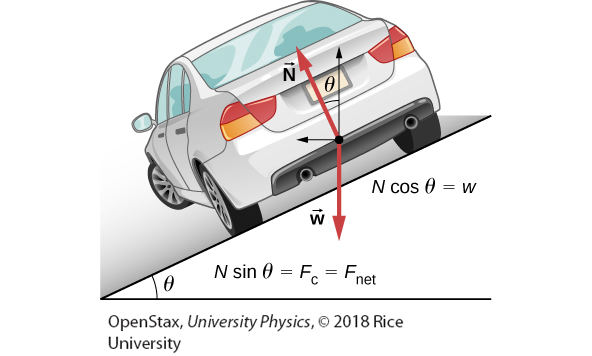
The car on this banked curve is moving away and turning to the left.

Ideal banking

sloping of a curve in a road, where the angle of the slope allows the vehicle to negotiate the curve at a certain speed without the aid of friction between the tires and the road; the net external force on the vehicle equals the horizontal centripetal force in the absence of friction.

Inverse tangent

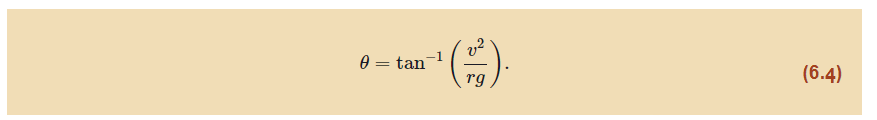
What determines the ideal speed for a banked curve without friction, and what is the formula to calculate it?

• For a frictionless banked curve, the ideal speed depends on:

  • Radius of the curve (r)

  • Banking angle (θ)

  • Acceleration due to gravity (g)

• Formula: v = √(rg tan θ)

• Key points:

  • This formula applies when no friction is needed (ideal banking)

  • Speed increases with:

    • Larger curve radius

    • Steeper banking angle

  • Example calculation: For a curve with r = 100.0 m and θ = 31.0°: v = √(100.0 m × 9.80 m/s² × 0.609) = 24.4 m/s ≈ 165 km/h

• Application:

  • Used in designing race tracks and test courses

  • Similar principles apply to airplane banking during turns

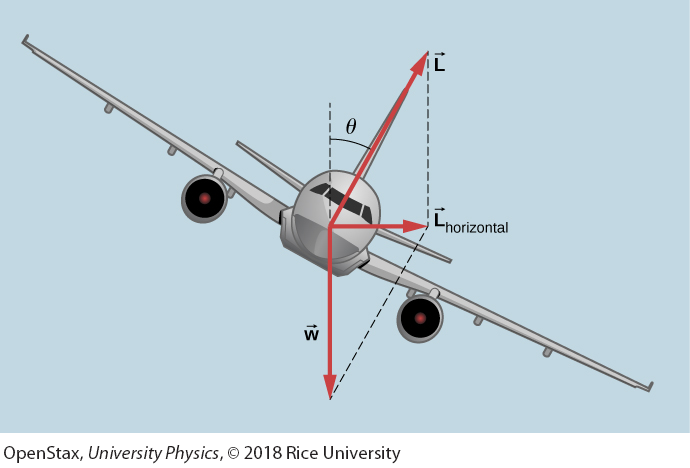
In a banked turn, the horizontal component of lift is unbalanced and accelerates the plane. The normal component of lift balances the plane’s weight. The banking angle is given by theta.

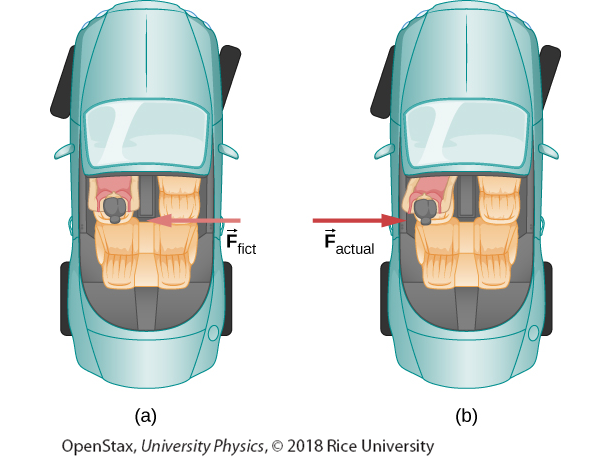
a. The car driver feels herself forced to the left relative to the car when she makes a right turn. This is an inertial force arising from the use of the car as a frame of reference.

b. In Earth’s frame of reference, the driver moves in a straight line, obeying Newton’s first law, and the car moves to the right. There is no force to the left on the driver relative to Earth. Instead, there is a force to the right on the car to make it turn.

noninertial frame of reference

accelerated frame of reference

Inertial force

Force that has no physical origin

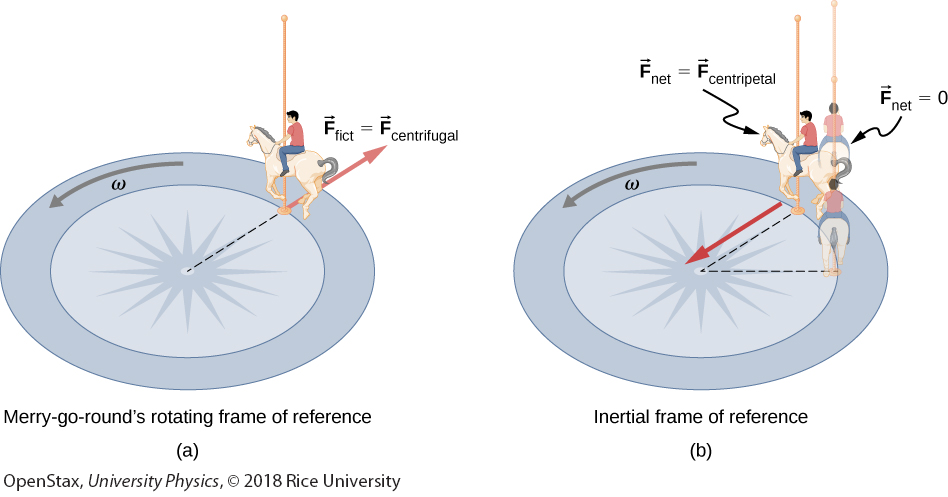
a. A rider on a merry-go-round feels as if he is being thrown off. This inertial force is sometimes mistakenly called the centrifugal force in an effort to explain the rider’s motion in the rotating frame of reference.

b. In an inertial frame of reference and according to Newton’s laws, it is his inertia that carries him off (the unshaded rider has F_net = 0 and heads in a straight line). A force, F_centripetal, is needed to cause a circular path.

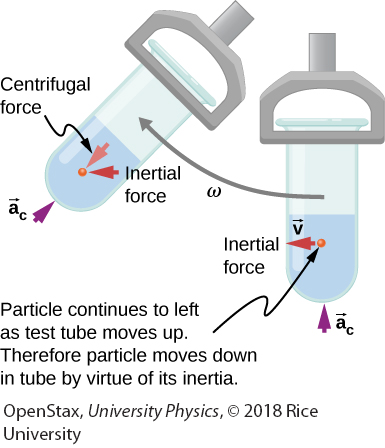
Centrifuges use inertia to perform their task. Particles in the fluid sediment settle out because their inertia carries them away from the center of rotation. The large angular velocity of the centrifuge quickens the sedimentation. Ultimately, the particles come into contact with the test tube walls, which then supply the centripetal force needed to make them move in a circle of constant radius.

Coriolis force

inertial force causing the apparent deflection of moving objects when viewed in a rotating frame of reference

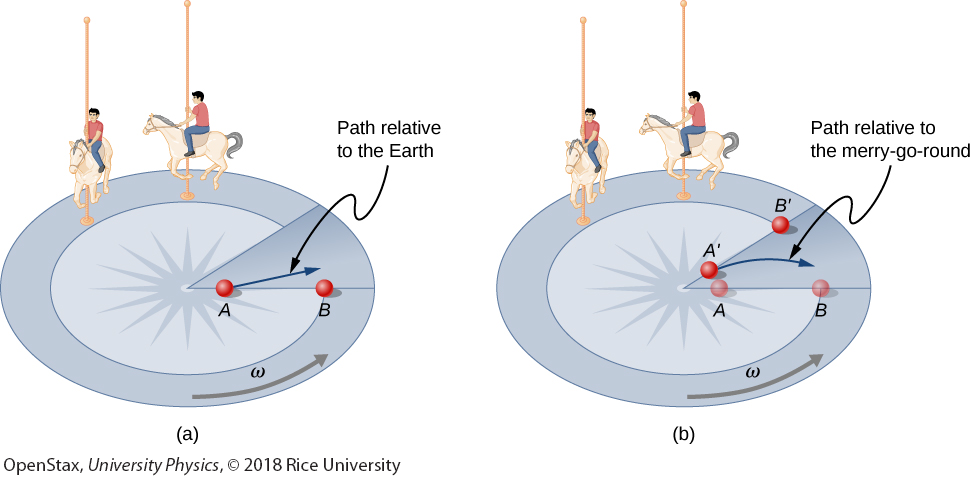
Looking down on the counterclockwise rotation of a merry-go-round, we see that a ball slid straight toward the edge follows a path curved to the right. The person slides the ball toward point B, starting at point A. Both points rotate to the shaded positions (A’ and B’) shown in the time that the ball follows the curved path in the rotating frame and a straight path in Earth’s frame.

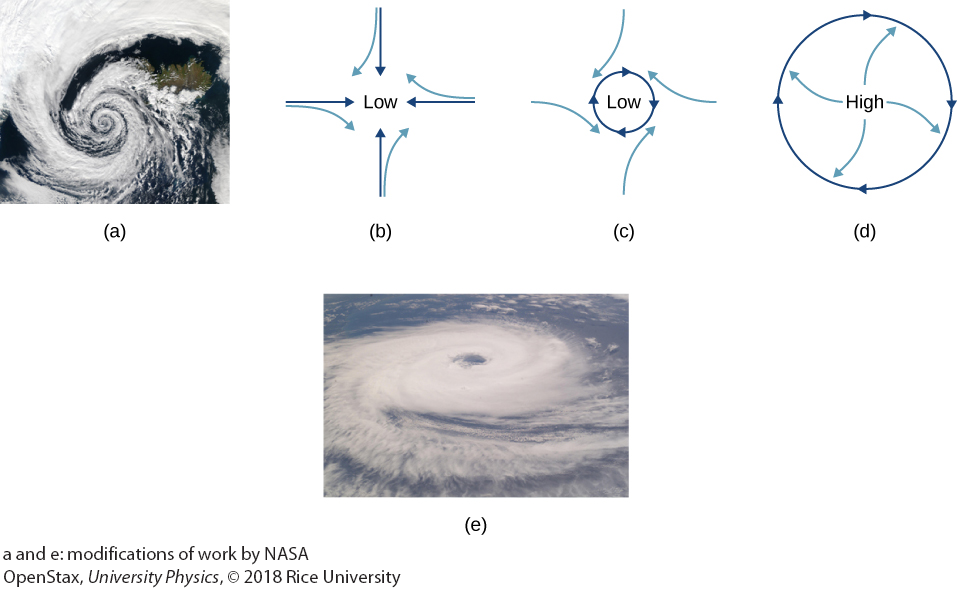
(a) The counterclockwise rotation of this Northern Hemisphere hurricane is a major consequence of the Coriolis force.

(b) Without the Coriolis force, air would flow straight into a low-pressure zone, such as that found in tropical cyclones.

(c) The Coriolis force deflects the winds to the right, producing a counterclockwise rotation.

(d) Wind flowing away from a high-pressure zone is also deflected to the right, producing a clockwise rotation.

(e) The opposite direction of rotation is produced by the Coriolis force in the Southern Hemisphere, leading to tropical cyclones.