MA225- Exam 3 Prep

Define what it means for a function to be Reflexive.

R is reflexive on 𝐴 if for all 𝑥∈𝐴, xRx.

Ex: S = {(x,y) ∈ R x R: x² = y²}

Proof

Let x be a real number. Then x²=x². Therefore xSx. Thus, S is reflexive on R.

Define what it means for a function to be Symmetric.

R is symmetric on 𝐴 if for all 𝑥,y∈𝐴, if xRy, then yRx.

Ex: S = {(x,y) ∈ R x R: x² = y²}

Proof

Assume that x and y are real numbers and xSy. Then x²=y². Therefore, y²=x². Thus ySx. We can conclude that S is symmetric on R.

Define what it means for a function to be Transitive.

R is transitive on 𝐴 if for all 𝑥,y,z∈𝐴, if xRy and yRz, then xRz.

Ex: S = {(x,y) ∈ R x R: x² = y²}

Proof

Assume that x, y, and z are real numbers and that both xSy and ySz. Then x²=y² and y²=z². Therefore, x² must also equal z². Thus, xSz. This proves that S is transitive on R.

When is a relation an Equivalence Relation?

When the relation is reflexive, symmetric, AND transitive.

What is the definition of a Function?

If and only if f is a subset of AxB and (x,y), (x,z) are elements of f is f a function.

What is the definition of a Function from A to B?

A function (or mapping) from A to B is a relation 𝑓 from A to B such that:

(i) the domain of 𝑓 is A

(ii) if (x,y) ∈ 𝑓 and (x,z) ∈ 𝑓, then y = z

𝑓: 𝐴→𝐵 is read as “𝑓 is a function from 𝐴 to 𝐵” or “𝑓 maps 𝐴 to 𝐵”. The set 𝐵 is called the codomain of 𝑓. In the case where 𝐵=𝐴, we say 𝑓 is a function on 𝐴.

When (x,y) ∈ 𝑓, we write y = f(x). We say that y is the image of 𝑓 at x and that x is a pre-image of y.

What makes a function Injective?

A function 𝑓 : 𝐴→𝐵 is an injection (or one-to-one) if whenever 𝑓(x)=𝑓(y), then x=y.

What makes a function Bijective?

A function 𝑓 : 𝐴→𝐵 is a bijection (or a one-to-one correspondence) if 𝑓 is one-to-one onto B.

What makes a function Surjective?

A function from A to B is a surjection (or onto B) if Rng(𝑓) = B. When 𝑓 is a surjection, we write that 𝑓 : A onto B.

Prove the Following Theorem (4.3.1):

If 𝑓 : 𝐴→𝐵 is onto 𝐵 and 𝑔 : 𝐵→𝐶 is onto 𝐶, then 𝑔∘𝑓 is onto 𝐶.

Prove the Following Theorem (4.3.3):

If 𝑓 : 𝐴→𝐵 is one-to-one and 𝑔 : 𝐵→𝐶 is one-to-one, then 𝑔∘𝑓 is one-to-one.

Assume the (𝑔∘𝑓)(x) = (𝑔∘𝑓)(z). Thus 𝑔(𝑓(x)) = 𝑔(𝑓(z)). Because 𝑔 is one-to-one, we have that 𝑓(x) = 𝑓(z). Because 𝑓 is one-to-one, we have that x = z. Therefore, 𝑔∘𝑓 is one-to-one.

Prove that the composite of two functions is a function.

Question 6a (Page: 172-173)

Prove the relation is an equivalence relation. Then give information about the equivalence classes as specified.

The relation S on R given by xSy iff x-y ∈ Q. Give the equivalence classes of 0, 1, and Sqrt(2).

Question 6b (Page: 172-173)

Prove the relation is an equivalence relation. Then give information about the equivalence classes as specified.

The relation R on N given by mSn iff m and n have the same digit in the tens place. Find an element of 106 that is less than 50; between 150 and 300; greater than 1,000. Find three such elements in the equivalence class 635.

Question 6c (Page: 172-173)

Prove the relation is an equivalence relation. Then give information about the equivalence classes as specified.

The relation V on R given by xVy iff x=y or xy=1. Give the equivalence classes of 3, 0, and -2/3.

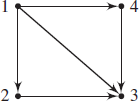
Question 8a (Page: 172-173)

Does the digraph represent a relation that is reflexive on the given set, symmetric, or transitive?

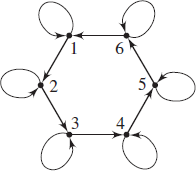
Question 8b (Page: 172-173)

Does the digraph represent a relation that is reflexive on the given set, symmetric, or transitive?

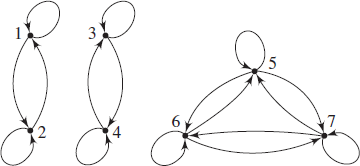
Question 8c (Page: 172-173)

Does the digraph represent a relation that is reflexive on the given set, symmetric, or transitive?

Question 9a (Page: 172-173)

Determine the equivalence classes for the relation of congruence module 2.

Question 9b (Page: 172-173)

Determine the equivalence classes for the relation of congruence module 8.

Question 9c (Page: 172-173)

Determine the equivalence classes for the relation of congruence module 1.

Question 10a (Page: 172-173)

Name a positive integer and a negative integer that are congruent to 0 (mod 5) and not congruent to 0 (mod 6).

Question 10b (Page: 172-173)

Name a positive integer and a negative integer that are congruent to 0 (mod 5) and congruent to 0 (mod 6).

Question 10c (Page: 172-173)

Name a positive integer and a negative integer that are congruent to 2 (mod 4) and not congruent to 8 (mod 6).

Question 1b (Page: 209-211)

Is the following relation a function? If so, give the domain and two sets that could be a codomain.

{(1,2),(1,3),(1,4),(1,5),(1,6)}

Question 1c (Page: 209-211)

Is the following relation a function? If so, give the domain and two sets that could be a codomain.

{(1,2),(2,1)}

Question 3a (Page: 209-211)

Identify the domain, range, and another possible codomain for each of the mapping below. Assume that the domain is the largest possible subset of R.

{(x,y) ∈ RxR: y = 1/x+1}

Question 3b (Page: 209-211)

Identify the domain, range, and another possible codomain for each of the mapping below. Assume that the domain is the largest possible subset of R.

{(x,y) ∈ RxR: y = x²+5}

Question 3c (Page: 209-211)

Identify the domain, range, and another possible codomain for each of the mapping below. Assume that the domain is the largest possible subset of R.

{(x,y) ∈ RxR: y = tan(x)}