COMP 2131- Module 2- Data Representation & Boolean Logic

Word size?

-the number of bits processed by a computer's CPU in one go

-eg. typically 32 bits or 64 bits

-Data bus size, instruction size, address size are

usually multiples of the word size

What are two conventions to store the values?

Little endian byte order

-Intel-compatible machines

Eg.

Assume x has the value 0x1234567

0x103 0x102 0x101 0x100 address

0x01 0x23 0x45 0x67 value

Big endian byte order

-Machines from IBM and Sun Microsystems

0x103 0x102 0x101 0x100 address

0x67 0x45 0x23 0x01 value

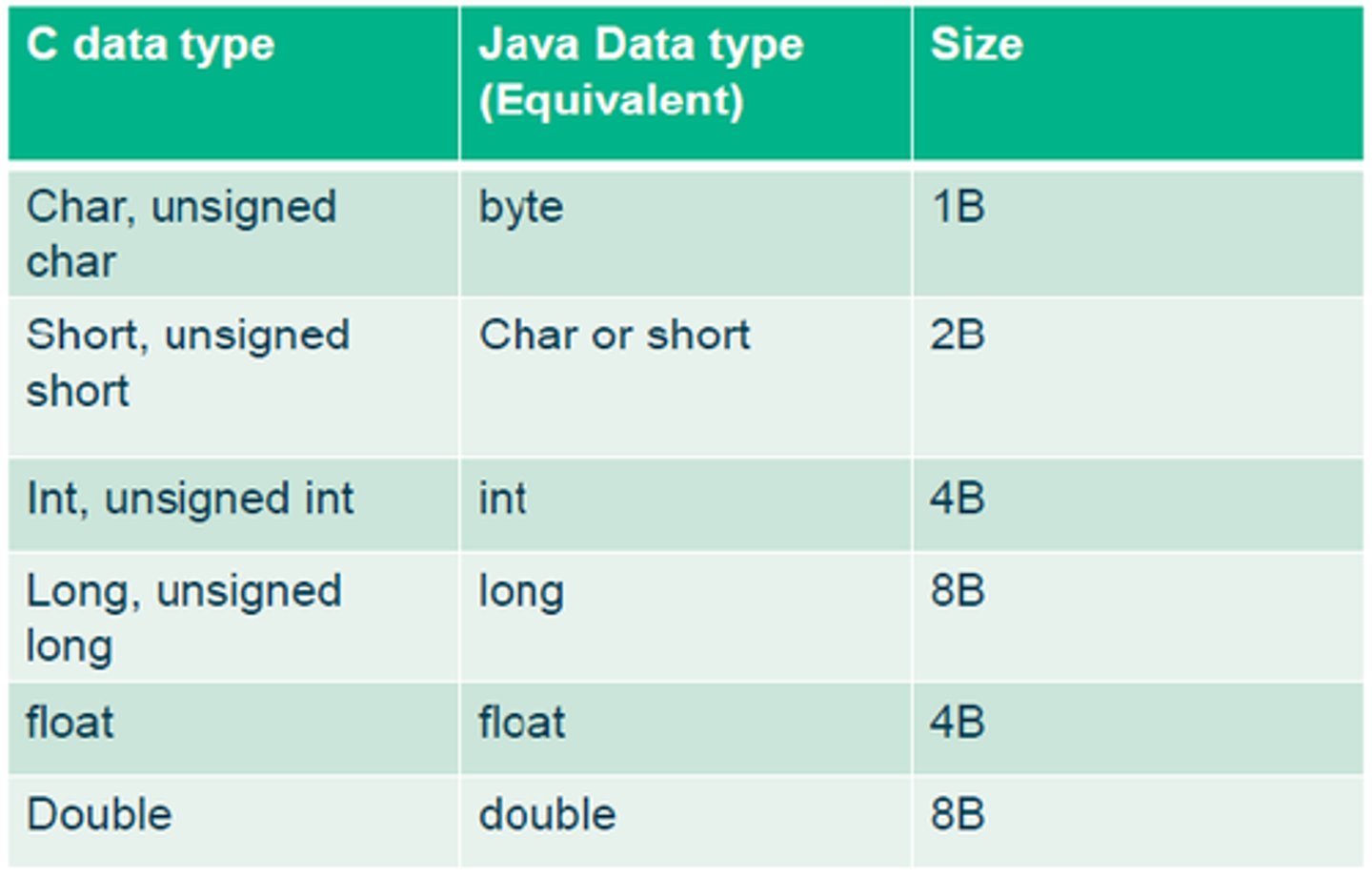
What is the size of each integer type below?

-Char (unsigned char)

-Short (unsigned Short)

-Int (unsigned Int)

-Long (unsigned Long)

-Float

-Double

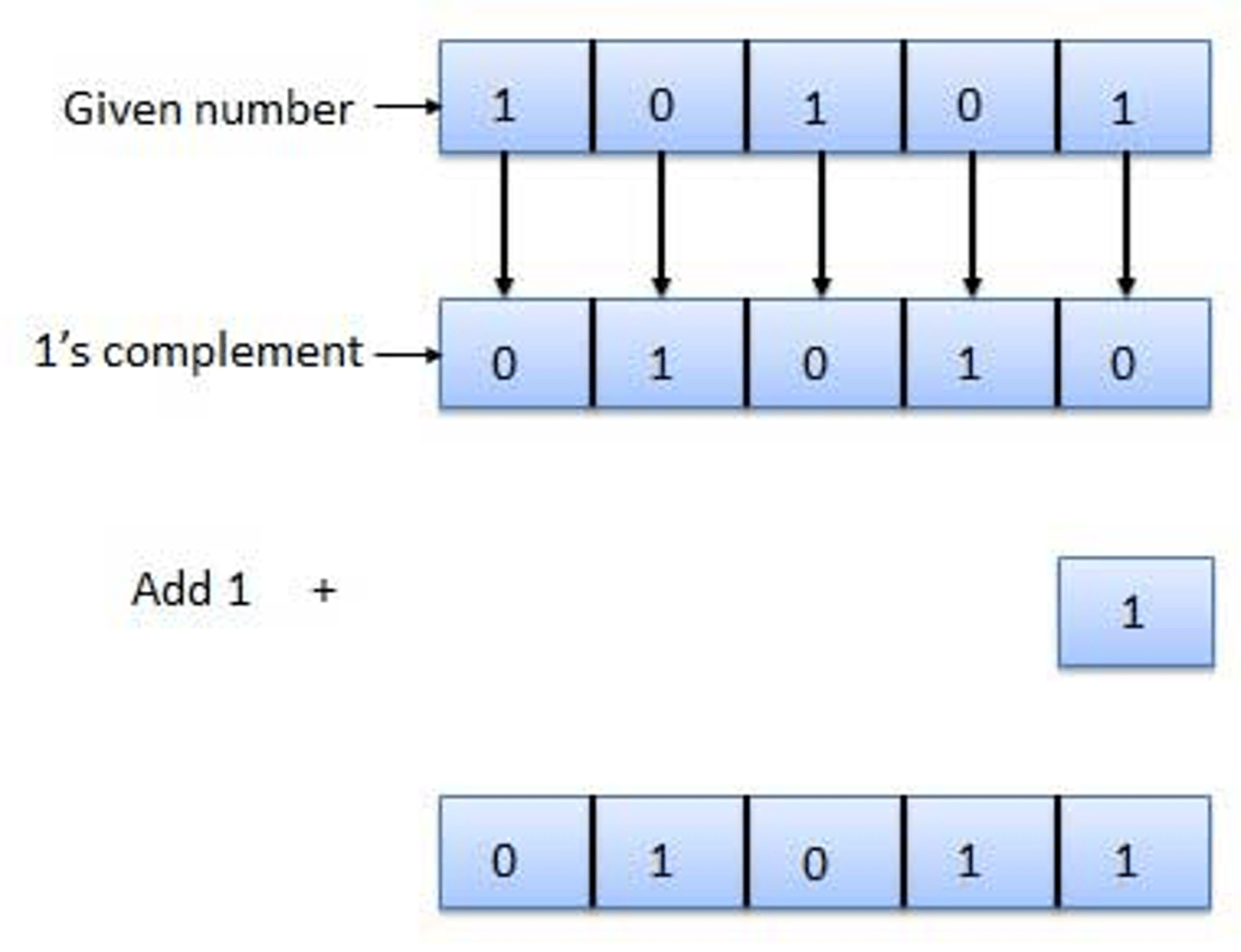
What is the method for subtraction?

-1's complement

-2's complement

How are signed integers represented in binary?

-2's complement for negative integers

Weight (in terms of Binary number systems)

(base)^position

Magnitude (in terms of Binary number systems)

Sum of "bit x weight"

Nibble

4 bits

Byte

8 bits

Magnitude (in terms of Octal number systems)

sum of "digit x weight"

Decimal to any base?

-Divide by base

How are fractional numbers represented in binary?

Fractional numbers in binary are represented using binary points, like decimal points in base 10. Each digit after the point represents a negative power of 2.

Example:
The binary number 10.101 means:

• 10 = 1×2^1 + 0×2^0 = 2

• .101 = 1×2^-1 + 0×2^-2 + 1×2^-3 = 0.5 + 0 + 0.125 = 0.625

• Total = 2.625

What are the three cases of single precision floating point values?

-Case 1 : Normalized Values

-Case 2 : Denormalized values

-Case 3 : Special values

Describe case 1: normalized values

A value where the leading bit of the mantissa is 1 (assumed, not stored).
Used for most non-zero floats to keep full precision.

Example:
Bits: 0 10000001 010...0

• Exponent: 129 → 2 (after bias)

• Mantissa: 1.01 = 1.25

• Value = 1.25 × 2^2 = 5.0

Describe case 2: de-normalized values

A value where the exponent is all zeros, and the leading bit of the mantissa is 0 (not 1).
Used for very small numbers close to zero.

Example:
Bits: 0 00000000 010...0

• Exponent = -126 (assumed)

• Mantissa = 0.01 = 0.25

• Value = 0.25 × 2^-126

Describe case 3: special values

When exponent = all 1s (255 in single precision):

• Mantissa = 0 → ∞ or -∞ (based on sign bit)

• Mantissa ≠ 0 → NaN (Not a Number)

Examples:

• 0 11111111 000...0 → +∞

• 1 11111111 000...0 → −∞

• 0 11111111 100...0 → NaN

What does ASCII stand for and what is it?

-American Standard Code for Information

Interchange

-It uses 7-bits to represent:

• 94 Graphic printing characters

• 34 Non-printing characters

What are the hexadecimal ASCII values for:

-Digits 0-9

-Upper case A-Z

-Lower case a-z

-Digits 0 to 9 span Hexadecimal values 0x30 to

0x39

-Upper case A-Z span 0x41 to 0x5A

-Lower case a-z span 0x61 to 0x7A

-Lower to upper case translation (and vice versa) occurs by flipping bit 6

What are the two categories of logic blocks?

-Combinational Logic (eg. Adders and multiplexors)

-Sequential logic (eg. Counter)

What are combinational logic circuits?

Circuits where output depends only on the current inputs, not on past inputs (no memory).

Examples:

• Adders

• Multiplexers

• Encoders

• Decoders

Key Point:
No feedback loops or storage elements—just logic gates!

What are the three main ways of specifying the function of a combinational logic circuit?

• Truth Table – Lists all input combinations and their corresponding outputs.

• Boolean Expression – Uses logic algebra to describe the relationship.

• Logic Diagram – A circuit made of logic gates showing how outputs are computed.

What is an asserted signal?

-A signal that is (logically) true, or 1

What is an deasserted signal?

-A signal that is (logically) false, or 0

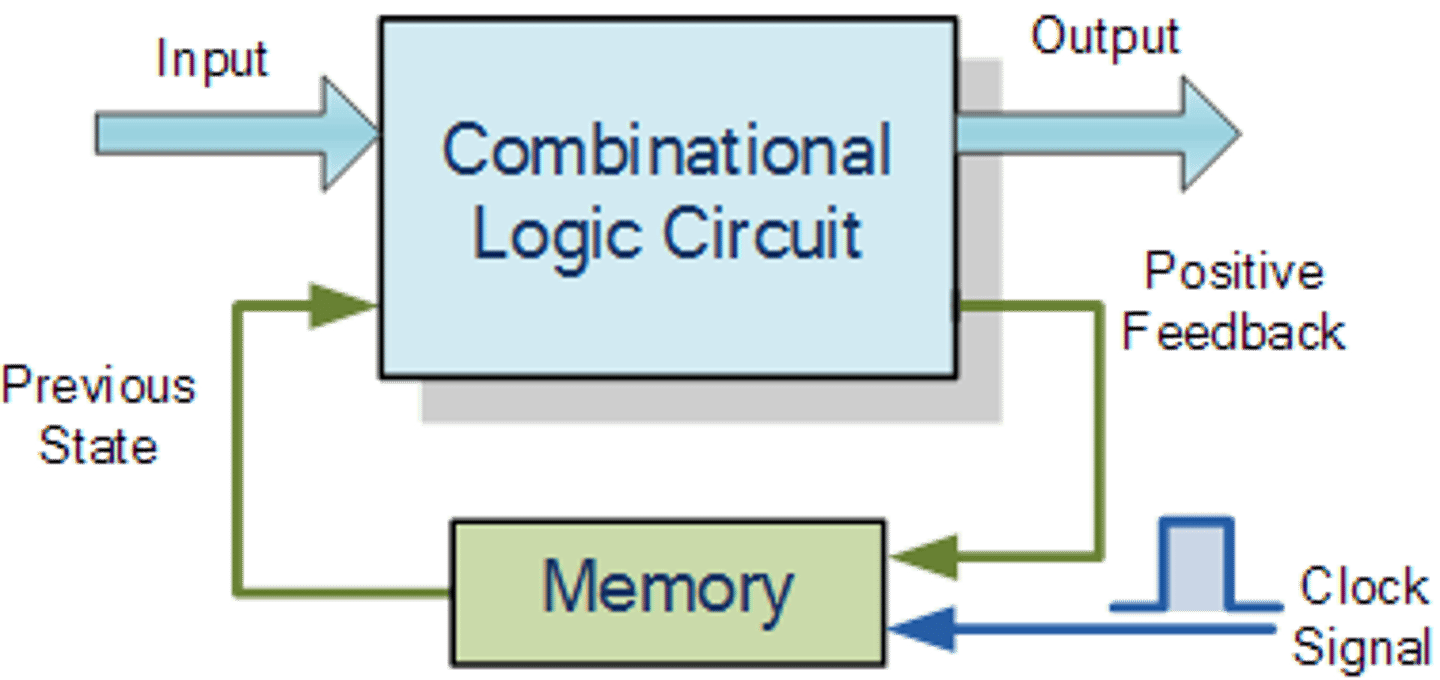
What are sequential logic circuits/blocks?

-A group of logic elements that contain memory

-The outputs can depend on both the inputs and the value stored in memory

What are the laws of Boolean algebra?

Identity law: A+ 0 =A and A · 1= A

Zero and One laws: A+ 1 = 1 and A · 0 = 0

Inverse laws: A+ NOTA= 1 and A · NOTA = 0

Commutative laws: A + B = B + A and A · B = B · A

Associative laws: A+ (B+C) = (A+B) +C

and A · (B · C) = (A · B) · C

Distributive laws: A · (B+C) = (A · B) + (A · C)

and A+ (B · C) = (A+B) · (A+C).

What is a decoder?

A decoder is a combinational circuit that converts n input lines into a maximum of 2ⁿ unique output lines. Only one output is active for each input combination.

Example:

• A 3-to-8 decoder takes 3 inputs and activates 1 of 8 outputs based on the binary input.

Use:
Used in memory address decoding, data routing, and control logic.

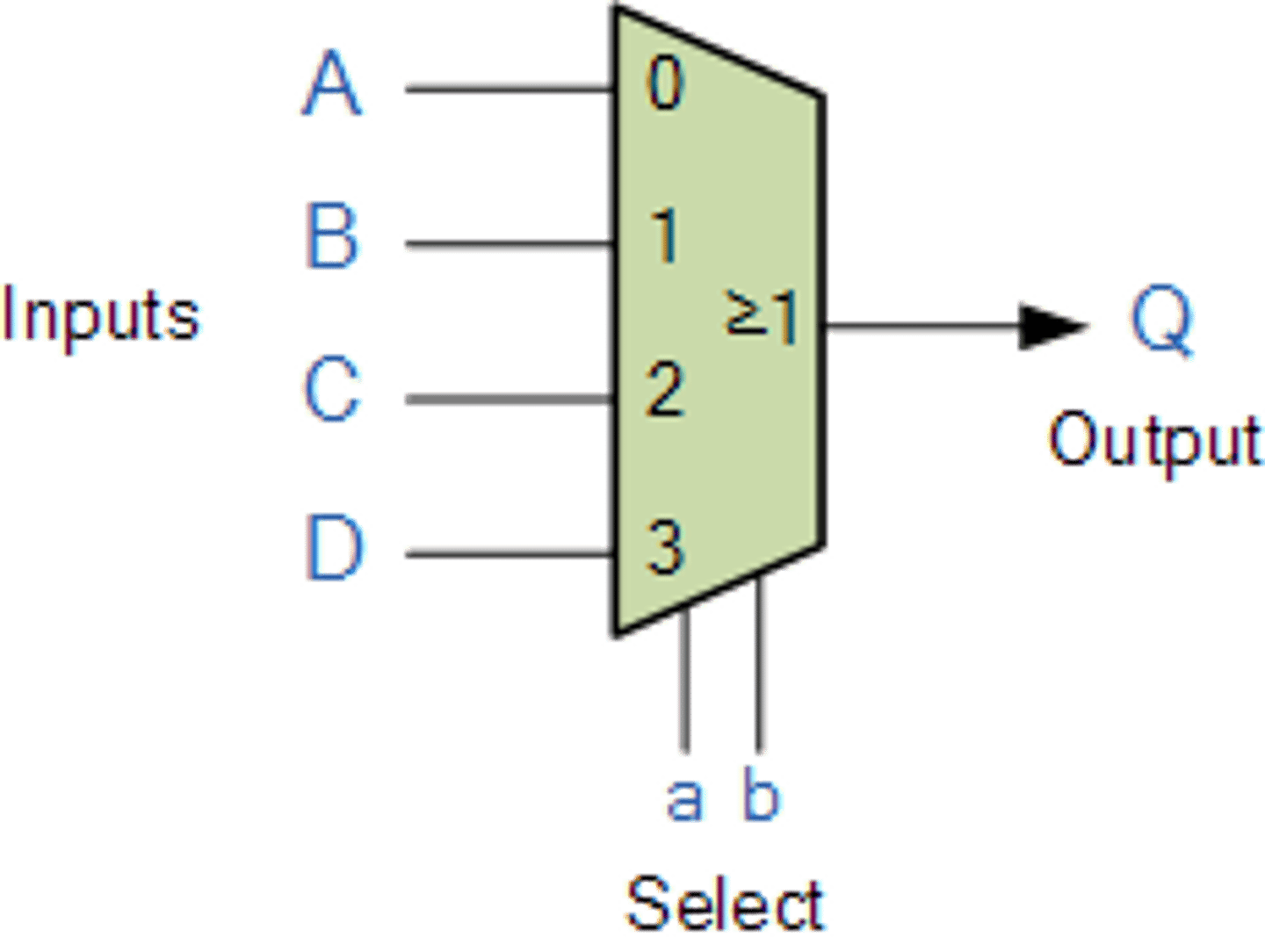
What is a multiplexor/selector?

-its output is one of the inputs that is selected by a control

-The selector (or control) value determines which of the inputs becomes an output

What are the two forms of two-level representation?

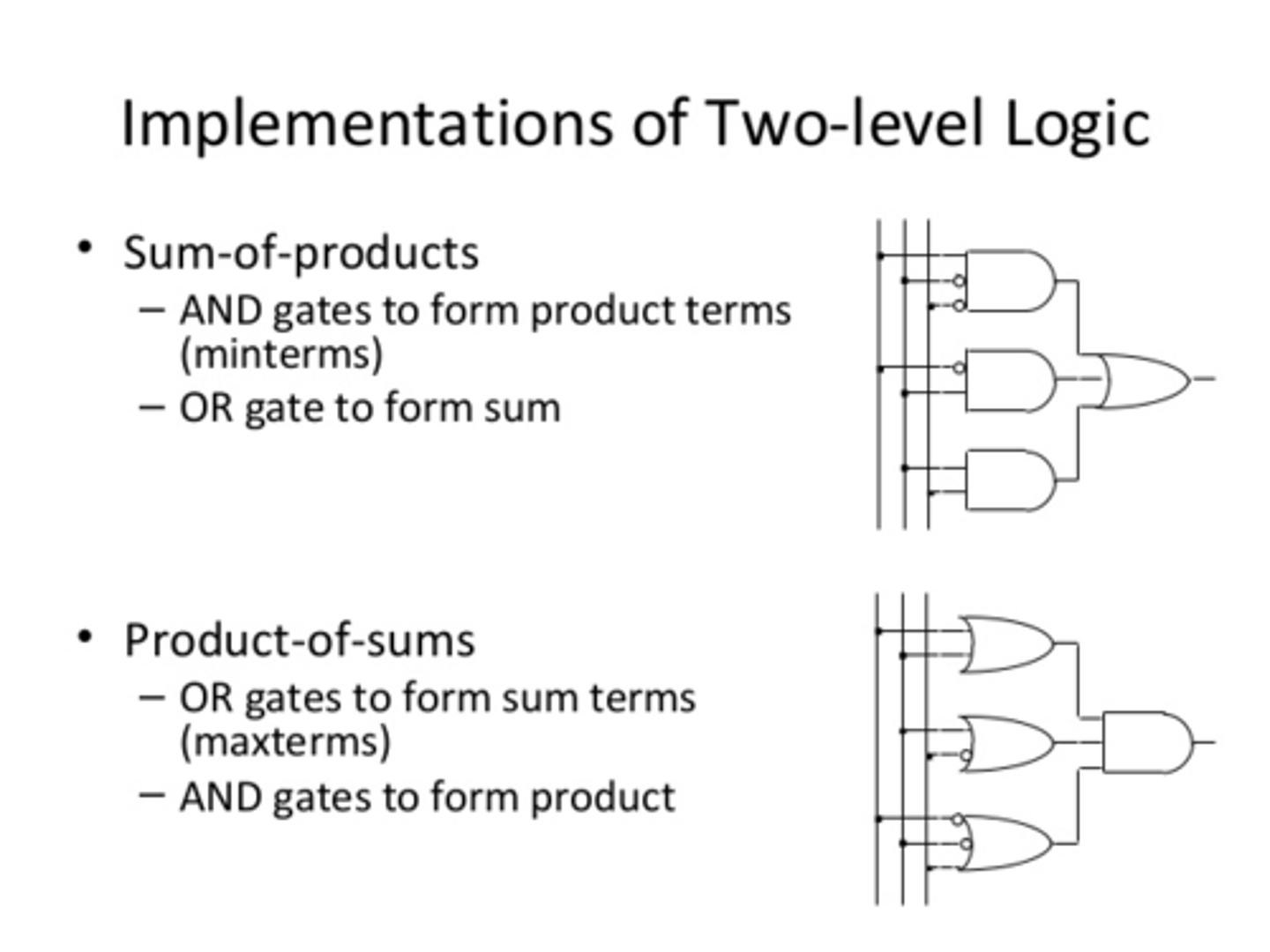
What is Sum of products (SOP)?

-A form of logical representation that employs a logical sum (OR) of products (terms joined using the AND operator)

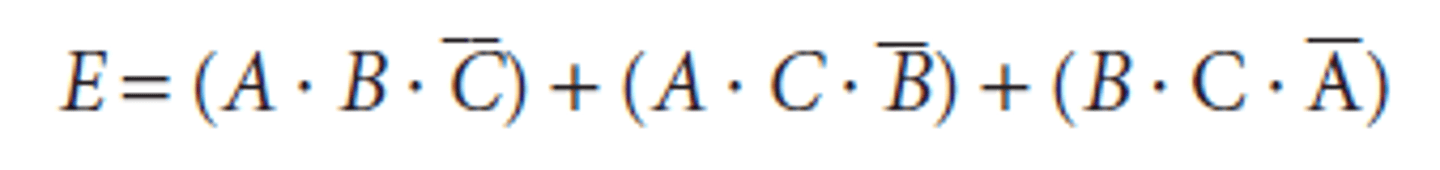
What is a progammable logic array (PLA)?

A PLA is a programmable digital device that can implement combinational logic circuits. It consists of a programmable AND array followed by a programmable OR array.

• The AND array generates minterms (product terms) of inputs.

• The OR array combines these minterms to produce the final outputs.

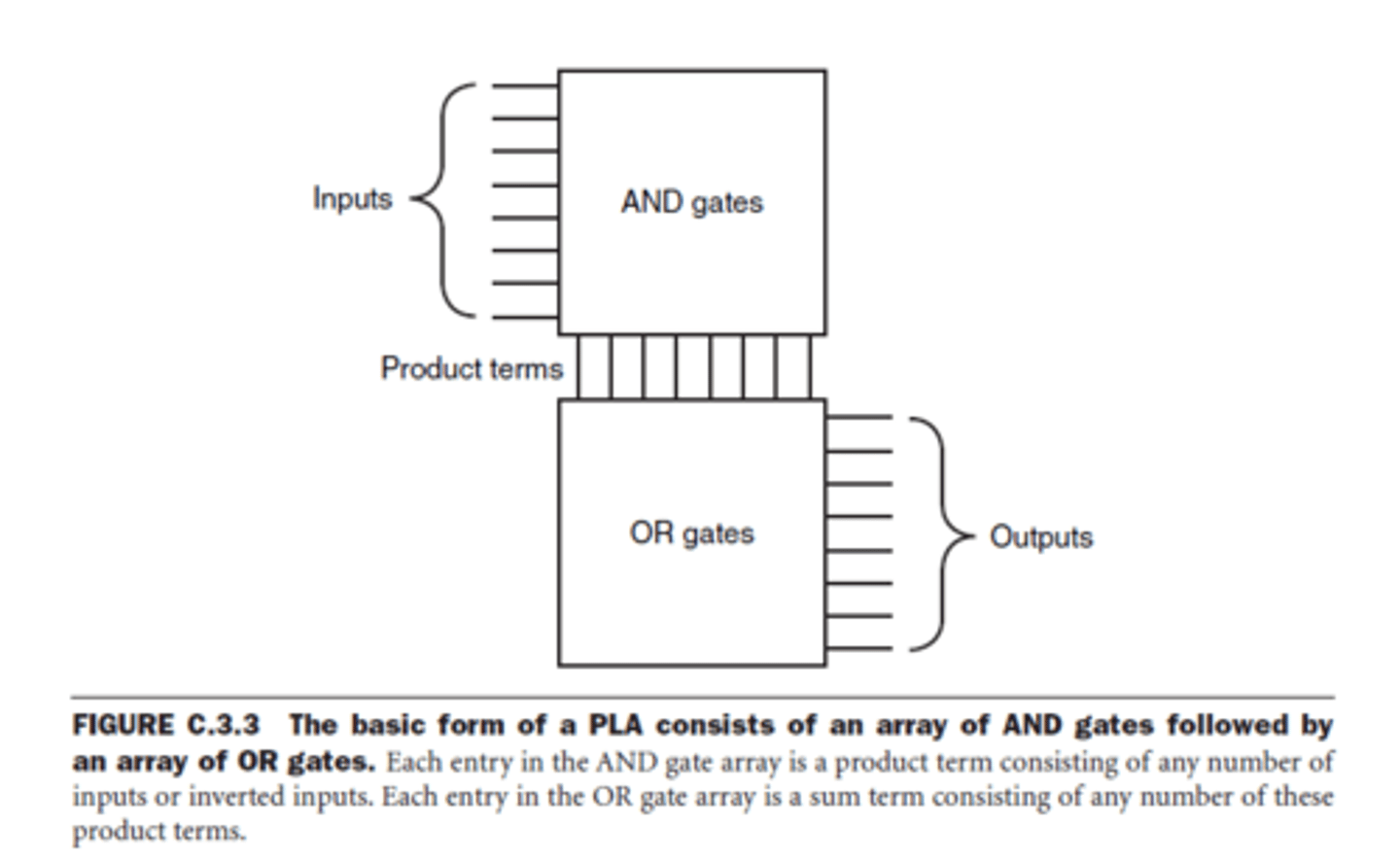
What are minterms (aka product terms)?

-The first stage in an array of AND gates form a set of product terms

-Each product term can consist of any of the inputs or their complements

Explain a logical shift right

-Fills the left end with k zeros

eg.

0110 0011 x>>4 (logical)

0000 0110

Explain an arithmetic shift right

-Fills the left end with k repetitions of the MSB

eg.

1001 0101 x>>4 (logical)

1111 1001