Precalculus CPM Chapter 1 Quiz Prep

Properties of Exponents (General)

For reference if this image is too small these rules can be found at CPM 1.1.2 Page 10

Factoring: Greatest Common Factor (GCF)

The largest factor that two or more numbers have in common.

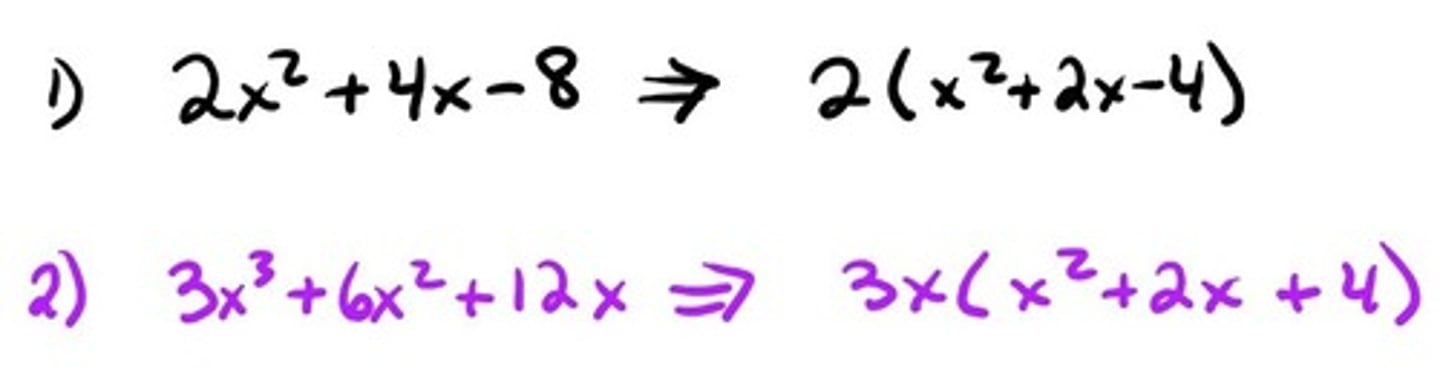
Using SohCahToa to solve for a side of a triangle

Sine of an angle is equal to the opposite side divided by the hypotenuse
Cosine of an angle is equal to the adjacent side divided by the hypotenuse
Tangent of an angle is equal to the opposite side divided by the adjacent side

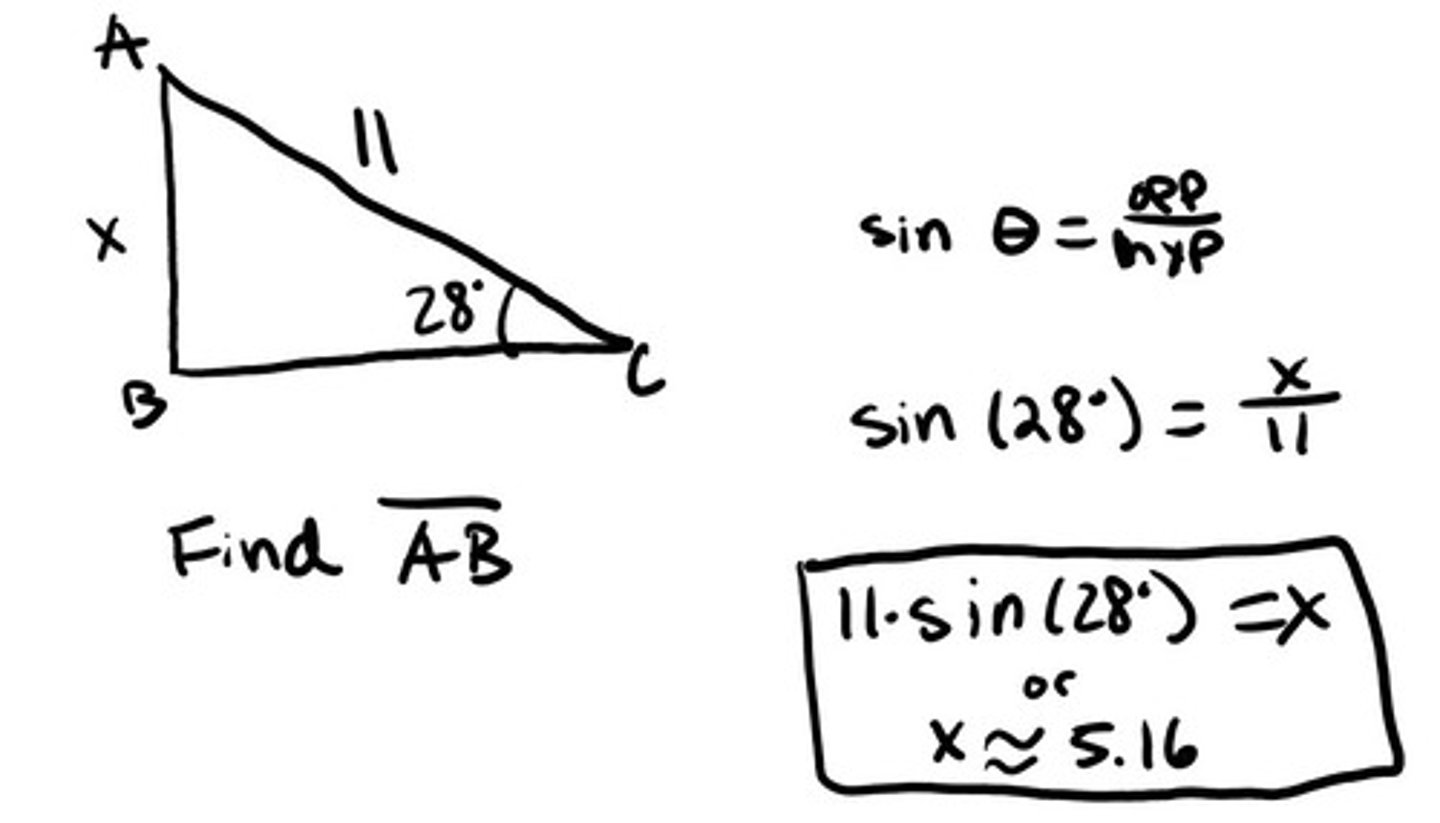
Multiplying Polynomials

Many use the box method or FOIL (distributive property) to multiply polynomials. Either can work but we need to know how to multiply polynomials

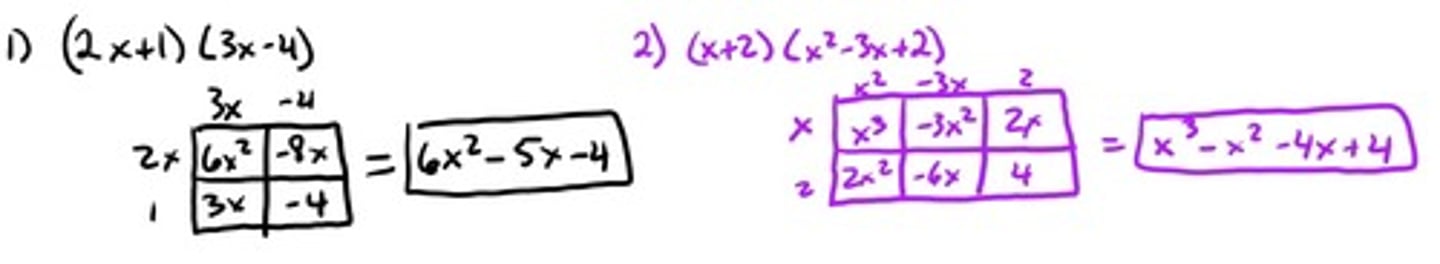
Simplifying Radicals (Cube Root and more)

Simplifying Radicals that are cube roots (and fourth roots, etc.) can be simplified similarly to square roots. The only difference is we need to match up factors in groups of 3 (or four etc.) to be able to "pull it out" of the radical. Anything that is pulled out, or left in should be multiplied back together in the end.

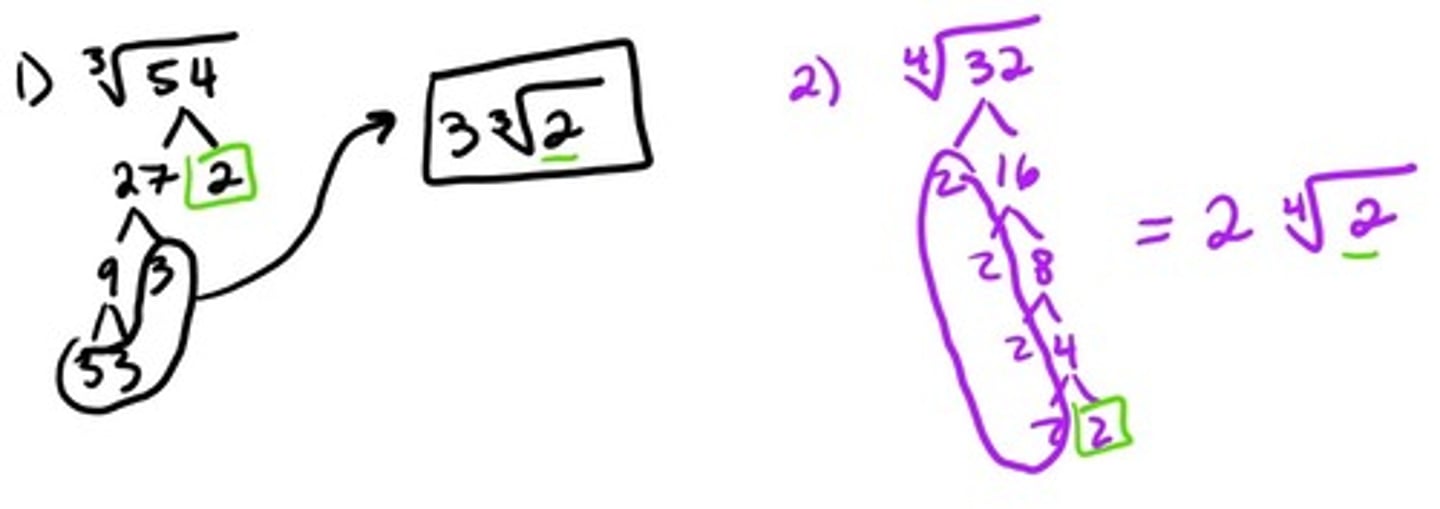
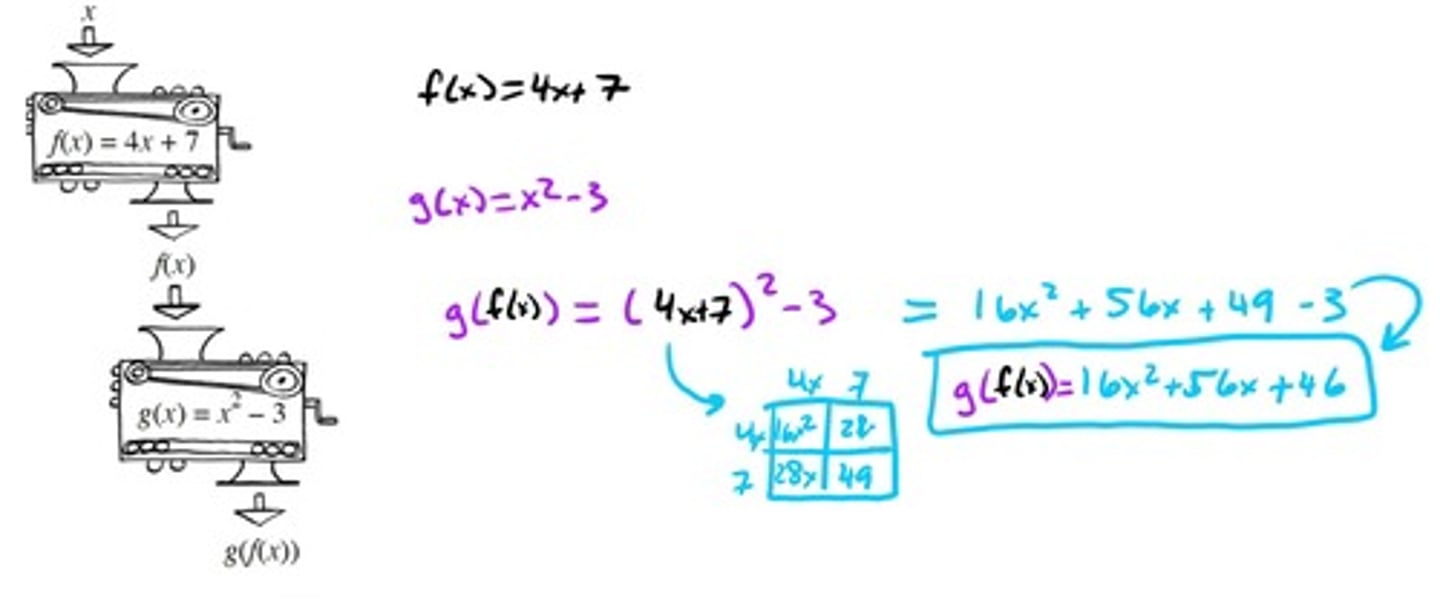
Composition (of two functions) 1.2.1 for image

If we plug in another function into f(x) we can just replace x with the entire function we are plugging in.

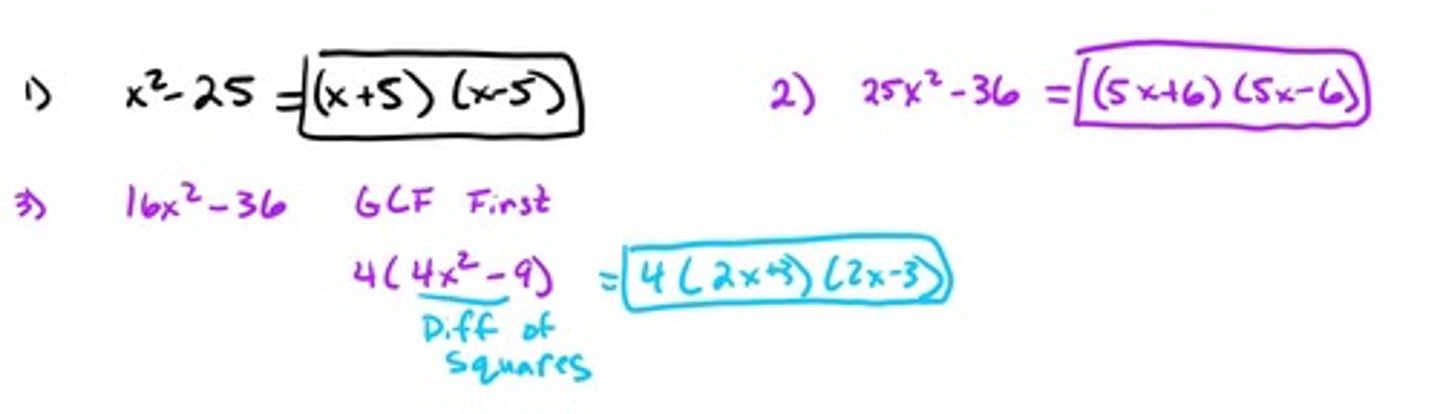
Factoring: Difference of Squares

a² - b² = (a - b) (a + b)If we have a binomial (two terms) and they are being subtracted AND they are both perfect squares we can use this formula to factor them quickly.

Point Slope Form

This is a helpful form to write a linear function when we are given points and can find the slope (or are given a point and the slope). The slope formula can be helpful when using this as well (y2-y1)/(x2-x1).
If this image is too small it can be found in your CPM book or website 1.1.6 Page 21

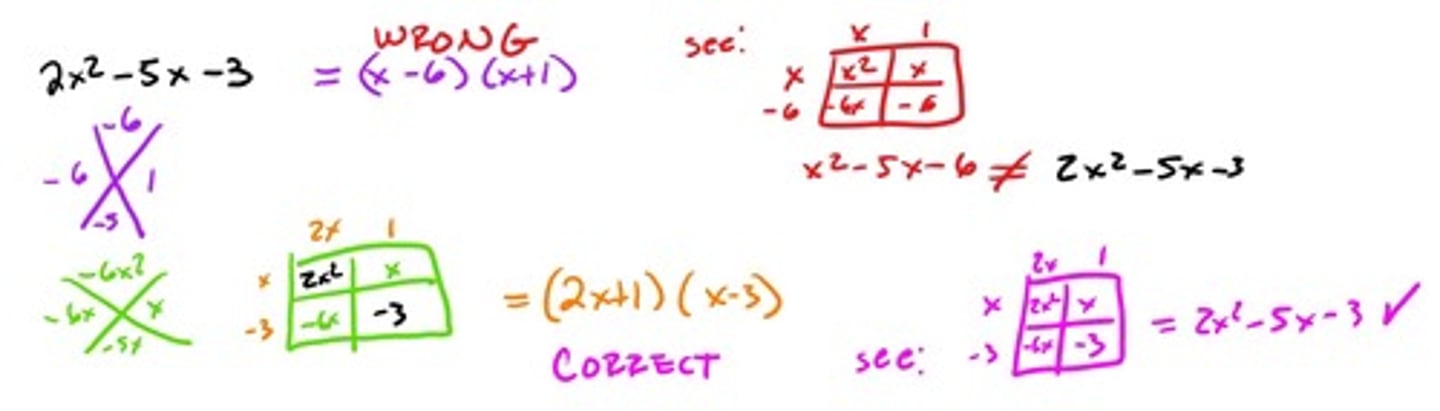
Factoring: Diamond/Box (a value not 1)

If the a value is not 1 and we skip the "Box" part of factoring we will not be factoring correctly.

Solving a Rational Equation for a Variable

-Get rid of the denominator by multiplying it on both sides-Distribute and get rid of any parentheses-move desired variable to one side (since you've distributed there will be multiply terms including that variable THAT'S OK)-move every other term to the opposite side-your GCF should now be the desired term you are solving for-divide both sides by whatever is now in parentheses

Simplifying Complex Fractions

If the image is too small this image can be found on CPM 3.1.3 on page 124

Polynomial Long Division (simple)

One way to divide two polynomials is to use long division. You first look at what you need to multiply to get from the first term of the outside to the first term on the inside (in this example it's 6 because 2x times 6 is 12x) then you multiply both outside terms by the number you chose. Then subtract. When you're left with a single digit we consider that our remainder and it because the numerator in our final answer. We subtract the two pieces because our remainder was negative. If our remainder was positive we would add the two.