12. The Normal Distribution Part I

A _________ random variable has infinitely many values, and those values are often associated with measurements on a continuous scale with no gaps or interruptions

continuous

A _______ ______ is a graph of a continuous probability distribution

density curve

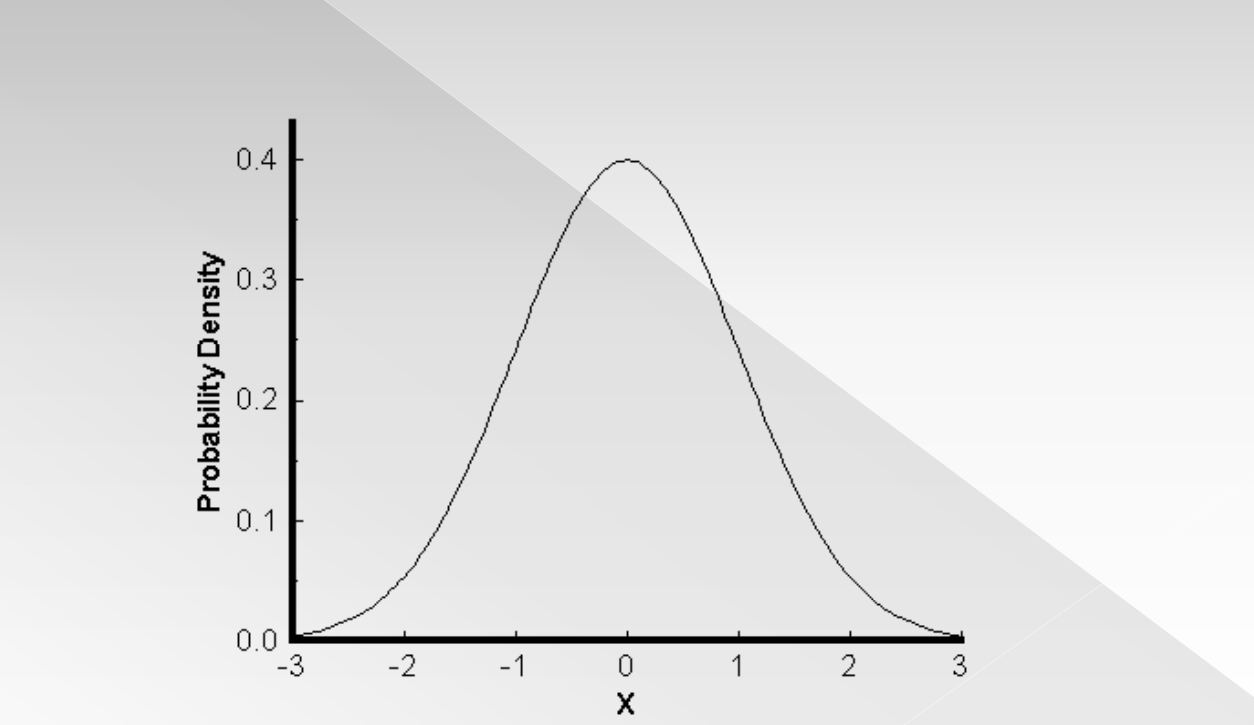
Continuous random variables are represented by ________ _______ _______ (pdf)

probability density functions

Probability density functions are used to compute ___________

→ Areas under the density curve (pdf) correspond to _____________

probabilities

The total area under a density curve must equal __

1

For continuous random variables, the probability that the random variable 𝑋 is equal to a single value, 𝑥 is always __

P(X = x) = __

0

Normal distributions are extremely important:

1) Moving forward, the statistical tests we will learn assume a normal distribution.

2) With a normal distribution, the mean and variance are ___ dependent on each other.

3) Many natural phenomena are approximately normally distributed (height, weight, blood pressure, etc)

not

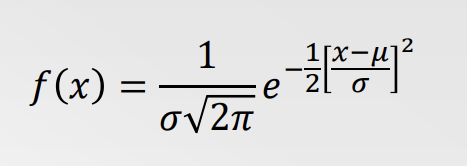
A continuous random variable has a normal distribution if:

→ It has a distribution with a graph that is __________ and bell-shaped, and

→ Can be described by the following probability density function (pdf) (we won’t use it)

symmetric

The Standard Normal Distribution has a mean of 0 and a standard deviation of __

1

Shorthand to describe normal RVs:

𝑿~𝑵 (𝝁, 𝝈)

where 𝜇 is the _____ and 𝜎 is the ________ _________ of the random variable 𝑋.

› 𝑿~𝑵 𝟎, 𝟏 signifies that 𝑋 is a normally distributed random variable with mean 𝜇 = 0, and standard deviation 𝜎 = 1.

› 𝒀~𝑵 𝟓, 𝟐 indicates that 𝑌 is a normally distributed random variable with mean 𝜇 = 5, and standard deviation 𝜎 = 2.

mean

standard deviation

The 68-95-99.7 rule is a helpful guide when working with normal random variables. This rule states that:

› About 68% (actually 68.26%) of all values fall within __ standard deviation of the mean.

› About 95% (actually 95.44%) of all values fall within __ standard deviations of the mean.

› About 99.7% (actually 99.74%) of all values fall within __ standard deviations of the mean.

1

2

3

All normal distributions are the same if we measure in units of size 𝜎 about the mean 𝜇 as center.

› Changing to these units is called ___________.

› To ___________ a value, subtract the mean of the distribution and then divide by the standard deviation

standardizing

standardize

If 𝑥 is an observation from a normal distribution that has mean 𝜇 and standard deviation 𝜎, the standardized value of 𝑥 is

𝑧 = ( 𝑥 − 𝜇 )/ 𝜎

› A standardized value is often called a _-score. › A _-score tells us how many standard deviations the original observation falls away from the mean, and in which direction

z

If a variable 𝑿 has any ________ distribution 𝑵 (𝝁, 𝝈) , then its standardized values have the standard normal distribution.

𝒁~𝑵 (𝟎, 1)

normal

Areas under a normal curve represent ___________ of observations from that normal distribution.

› They also represent probabilities of randomly selecting an individual from that normal distribution.

› There is not a direct formula for areas under a normal curve.

Must use either a software or a table

proportions

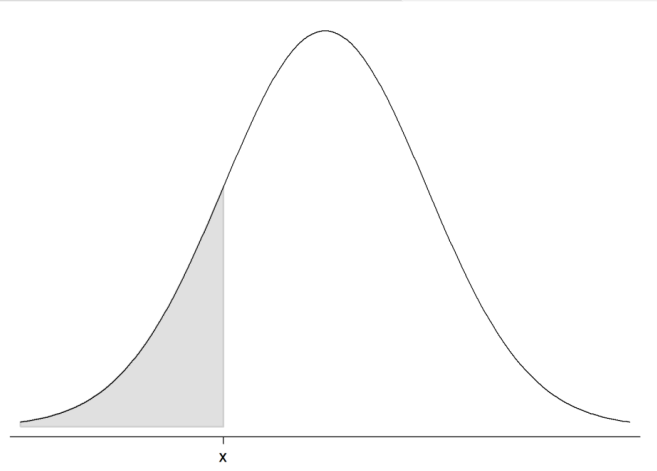
Most software and tables give ________ probabilities.

› The __________ probability for a value 𝑥 in a distribution is the proportion of observations in the distribution that lie at or below 𝑥.

cumulative