2: symmetry and bonding

define

• symmetry element

• symmetry operation

element = geometrical feature i.e. point, axis, plane

operation = act of moving in space w.r.t. element i.e. rotation about an axis, reflection in a plane, inversion in/through a point

what are the 5 kinds of symmetry operations

• proper rotations

• reflections

• identity

• improper rotations

• inversion

describe proper rotations

C(n)

rotation about an axis by 360/n

there are (n-1) rotations for any C(n) axis

what is the principal axis of rotation

C(n) with highest value of n

describe reflections

σ(v) = reflection plane containing principal axis of rotation

σ(h) = reflection plane perpendicular to principal axis of rotation

σ(d) = reflection plane diagonal to principal axis of rotation

describe identity

E = doing nothing to an object

σ² = i² = E

describe inversion

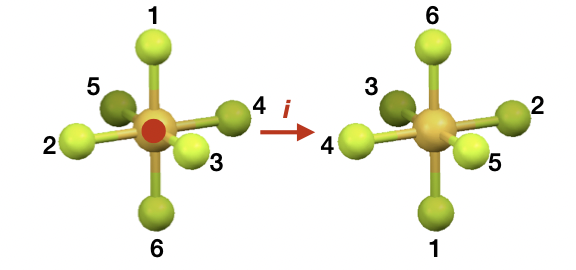
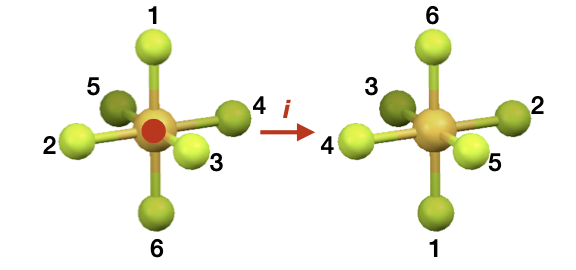
describe improper rotations

composite operation = rotation around principal axis and reflection in σ(h)

describe the process of assigning point groups

• principal axis of rotation

• perpendicular C2 axis?

yes:

= D

σ(h) = Dnh

σ(d) = Dnd

or Dn

no:

σ(h) = Cnh

σ(v) = Cnv

S2n (improper rotation w.r.t to C2 axis) = S2n

or Cn

σ(h) takes precedent

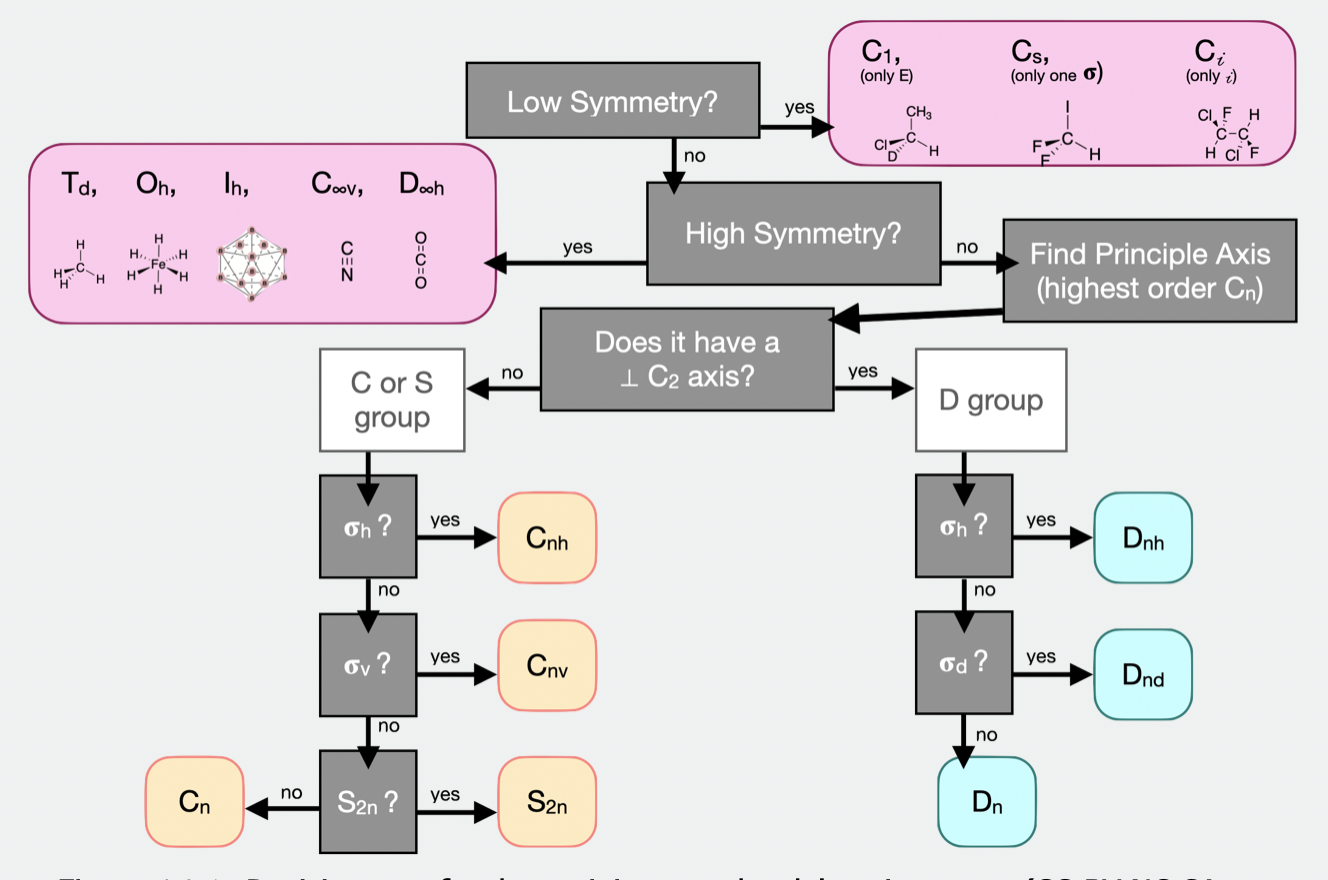
what are the low symmetry point groups?

no symmetry (only E) = C1

only σ = Cs

only i = Ci

what are the high symmetry point groups?

tetrahedral = Td

octahedral = Oh

isohedral = Ih

linear with same end = D∞h

linear with different end = C∞v

what is a group in group theory?

collection of elements that obey certain well-defined criteria

what is a point group w.r.t. group theory?

an objects symmetry operation form a point group, where the group operation “ ° “ is understood to be the successive application of symmetry operations

what is the criteria of group theory?

• closure

= results of two elements by an operation is another element

• identity

= set includes an identity element which leaves another element unchanged after operation

• inverse

= each element has an inverse which returns element to identity after operation

• associativity

( A ° B ) ° C = A ( B ° C )

(generally not commutative)

what are group multiplication tables?

to obey the closure criteria, application of two subsequent symmetry operations must be equivalent to a single symmetry operation

form the group multiplication table for C(2v)

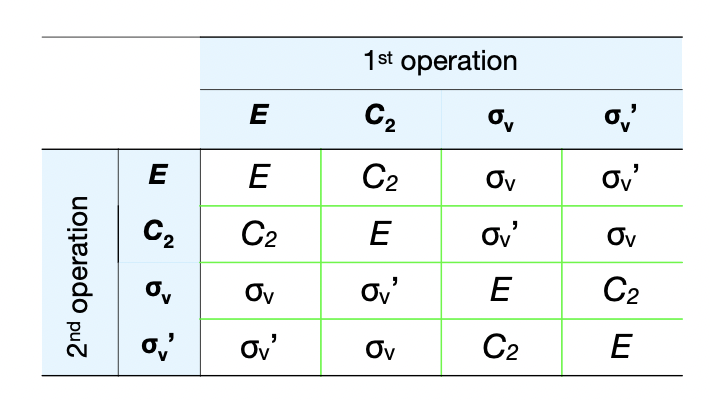
in what order are symmetry operations applied

successive operations are written from right to left i.e. apply operation to whats on its right first

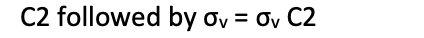
how do wavefunctions have a sign?

they change sign between different regions of space
probability = square of the wavefunction

hence, sign is not observable

what is a character?

= X
= defines how a feature/property (typically an orbital) is affected by a particular symmetry operation

what are the possible characters?

+1 = no change
0 = moves
-1 = no change, sign flip

what is an invariant point?

= point which does not move upon application of symmetry operations

what is a representation?

= Γ

= the complete set of characters for a particular feature/property from application of all symmetry operations

= encapsulates the symmetry behaviour of a feature/property

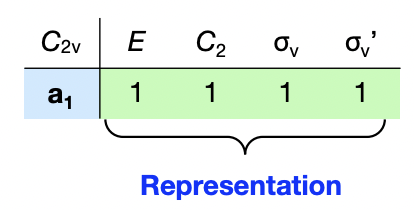
what is a Mulliken symbol

= a label for a (irreducible) representation

how can we describe the symmetry of a particular feature/property?

the ‘feature/property’ on X forms a basis for the ‘Mulliken symbol’ of the ‘point group’

what is a character table?

lists all the irreducible representations of a point group

what is meant by ‘classes of symmetry operations’?

symmetry operations in character table can be multiples = a class of the symmetry operation

the character in the irreducible representation refer to classes of symmetry operations = single character = SUM THE RESULTING CHARACTERS

how can the orbitals represented by a symmetry species be determined?

by the right hand column

describe the linear combination of atomic orbitals (LCAO)

the many electron wavefunction of a molecule is constructed from the one electron wavefunctions

orbital = one electron wavefunction

atomic orbital = one electron wavefunction of an atom

molecule orbital = many electron wavefunction of a molecule

how does wavefunction interference arise?

overlapping of atomic orbitals

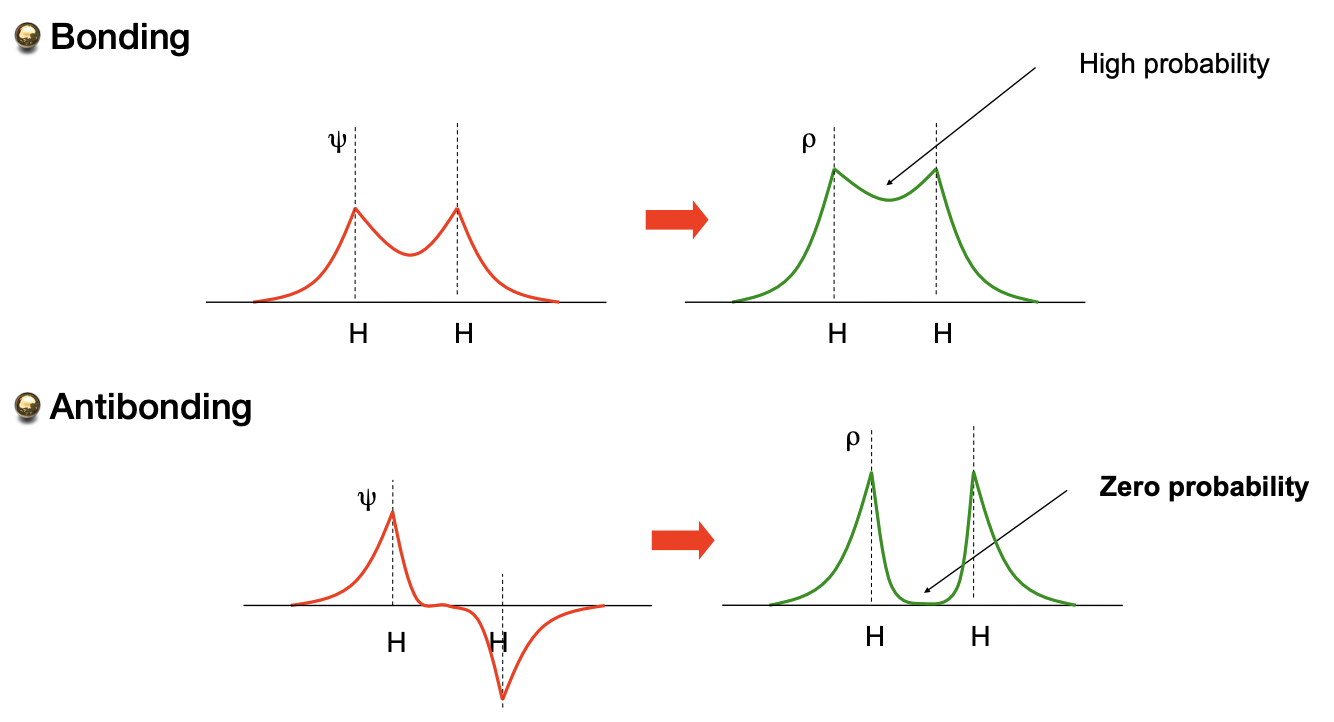
describe the two types of wavefunction interference

constructive = bonding MO

destructive = anti-bonding MO

describe the probability of finding an electron in bonding/anti-bonding MOs

BMO = finding an electron between nuclei is increased w.r.t separated AOs

ABMO = finding an electron between nuclei is decreased (=0) w.r.t. separated AOs

define the overlap integral

interference and the formation of bonding/anti-bonding orbitals is a result of AO overlap. the overlap integral quantifies the overlap

*not given*

how can symmetry be used to simplify the evaluation of integrals

symmetry tells us which integrals ‘vanish’ (= 0) → which bonding does not occur → non-bonding

if the integral does not vanish (> 0) → calculation to find overlap integral

describe how to construct an MO diagram for a polyatomic

• generate SALC and reduce

• assign symmetry species (invariant + SALC)

• only orbitals of the same symmetry can interact

2 orbital interaction = anti-bonding and bonding

3 orbital interaction = anti-bonding, non-bonding, bonding

closer in e AOs = larger interaction

no. of AOs = no. of MOs

what is a SALC?

symmetry adapted linear combination

describe how to generate a SALC

• apply each symmetry operation to each orbital in turn

+1 = no change

0 = moves

-1 = no change, sign flip

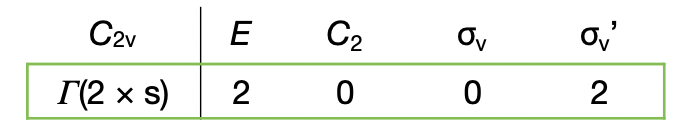
• sum the characters to give a character table of the reducible representation (pictured)

• reduce by either 1) reduction by inspection or 2) reduction formula

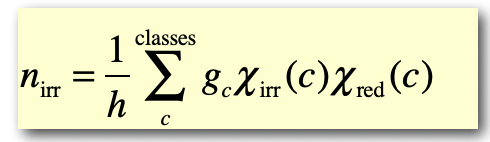
what do the characters in the reduction formula represent?

n(irr) = number of times the irreducible representation occurs in the reducible representation

h = order of the group = total number of symmetry operations =

g(c) = number of symmetry operations in class c

X(irr)(c) = character of class c in the irreducible representation

X(red)(c) = character of class c in the reducible representation

checks:

n(irr) > 0

the dimension (= character under E = number of orbitals combined) = sum of dimensions of the irreducible representations it reduces to

Γ = symmetry species + symmetry species

the ‘orbitals’ form a basis for the ‘symmetry species’ representations in ‘point group’.

describe how to assign symmetry species at an invariant point

s-orbital = ALWAYS totally symmetric symmetry species

other orbitals = read from table

i.e. p(x) = x in table

p(y) = y in table

p(z) = z in table

describe how to determine the shape of SALCs

1. guess

i.e. add and subtract

2. projection operators

describe how to determine the shape of SALCs via projection operators

1. label the orbitals involved i.e. s1, s2, …

2. select one orbital and for each symmetry operation, note which orbital it is converted into

3. multiply each “result” by corresponding character in each symmetry species

4. sum the result to give the linear combination

what do symmetry species e and t mean?

e = accounts for 2 orbitals which are double degenerate

t = accounts for 3 orbitals which are triply degenerate

what does it mean when two features/properties (orbitals) have the same symmetry species?

they are degenerate

symmetry operations must leave the physical properties, including energy, unchanged

what happens when there are >1 (n) degenerate orbitals contributing to a MO?

the resulting MOs (bonding, anti-bonding, non-bonding) are (n) degenerate

describe how to determine the shape of SALCs via projection operators for degenerate orbitals

1. label the orbitals involved i.e. s1, s2, …

2. select one orbital and for each symmetry operation, note which orbital it is converted into

3. multiply each “result” by corresponding character in each symmetry species

4. sum the result to give the linear combination

5. repeat 2-4 for the other orbitals we have labelled

6. sum (MINUS) the result

describe Walsh/correlation diagrams

= shows how the electron structure (MO diagram) varies as a function of a change in molecular structure

y = energy

x = structural coordinate = often bond angle

why do the orbitals between linear and triangular 3H have different energies?

= increasing/decreasing overlap

linear = less overlap possible = more anti-bonding = higher E

triangular = more overlap possible = less anti-bonding = lower E

how is the optimal number of electrons for a molecule found?

fill all the bonding and non-bonding MOs; leave the anti-bonding MOs empty

i.e.

linear H3 = 4e- optimal = H3(-)

triangular H3 = 2e- optimal = H3(+)

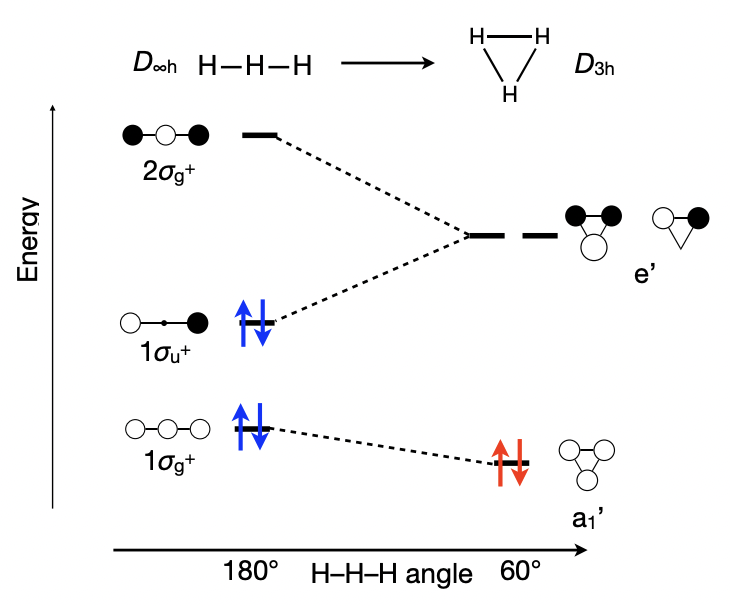
what is Walsh’s rule?

a molecule adopts the structure that best stabilises its HOMO

= hence, changes in the number of electrons can trigger structural change

what type of transition does UV/Vis spectroscopy monitor?

electronic

what is the intensity of electronic transitions defined? *given*

gs = ground state wavefunction

es = excited state wavefunction

μ^ = electric dipole moment operator

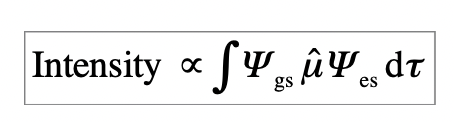
how can group theory be applied to electronic spectroscopy?

= to identify where the integral (of intensity) vanishes (=0) for symmetry reasons

integral vanishes (=0) = transition is dipole-forbidden for symmetry reasons

integral does not vanish (>0) = transition is dipole-allowed

what is the selection rule of a transition being dipole-allowed for symmetry reasons?

a transition is dipole allowed, if and only if, the triple product (of reducible representations) contains the totally symmetric representation

Γgs = symmetry (species) of the ground state

Γes = symmetry (species) of the excited stae

Γ(μ) = symmetry (species) of the dipole-moment operator

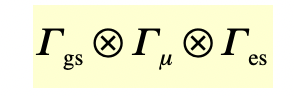
what is the Γ of an electronic state

= direct product of each and every symmetry species of each electron (= AO/MO it occupies)

Γgs = configuration before transition

Γes = configuration after transition

filled/empty orbitals = symmetric = +SS (x) (-SS) = completely symmetric symmetry species

[ SS = symmetry species ]

what is the direct product of 2 symmetry species?

multiply each character in a symmetry species with the equivalent character in the other symmetry species

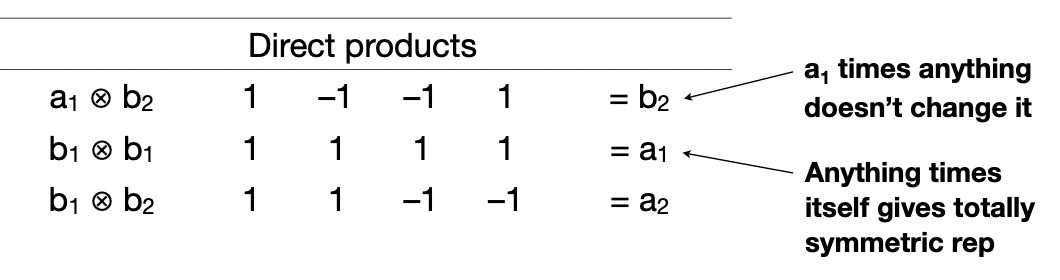
what is the symmetry of the dipole-moment operator, Γ(μ)?

= same symmetry as the x, y, and z in the point group

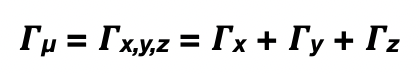
what are the 2 types of spectroscopy measuring bond vibrations?

• IR

• raman

describe IR spectroscopy

(lower = IR region) energy photon is absorbed by the molecule and excites a vibration

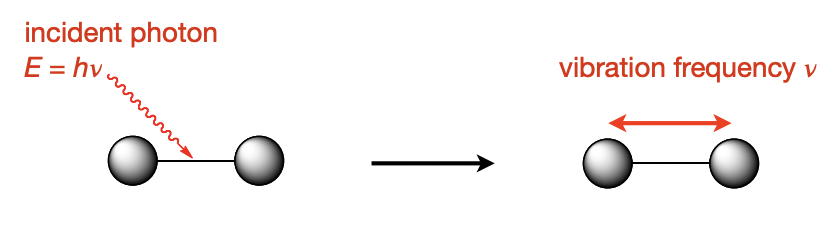
describe raman spectroscopy

(higher = Vis region) energy photon is scattered by the molecule

= the molecule absorbs some energy which triggers vibration

= outgoing photon has lower energy than the incident one

how can group theory be applied to vibrational spectroscopy?

vibrations are displacement of atoms

use Cartesian displacement vectors as a basis to construct representations

describe how to construct a Cartesian displacement reducible representation

1. determine the point group

2. place the molecule in the Cartesian coordinate system as defined by the character table

   principle rotational axis = z-axis

   plane of page = y-axis

3. apply Cartesian coordinate system to each atom

4. determine the character of applying each symmetry operation to each Cartesian basis vector (=axis) to each atom

5. reduce into sum of irreducible representations by reduction formula

what are the 3 types of displacement?

• translations

• rotations

• vibrations

what does the Cartesian displacement reducible representation span?

all 3 types of displacement

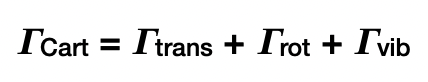
how can the symmetry of translation and rotations be determined?

= in the character table

x, y, z = translations

R(x, y, z) = rotations

how can the symmetry of vibrations be determined?

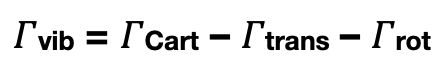
what does a Γ(vib) = 2a1 + b2 mean?

there are two distinct vibrational modes

1 vibrational mode = 1 symmetry species

what is the selection rule of a vibration being IR-active for symmetry reasons?

for any process that involves the absorption of light, the transition is allowed, if and only if, the triple product contains the totally symmetric representation

Γgs = always totally symmetric ~ 1

Γes = Γvib = TREAT EACH VIBRATION SEPARATELY

Γ(μ) = sum of x, y, and z representations in the point group

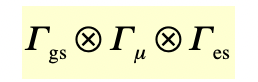
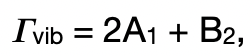
describe the IR-active transition in C2v

a1: IR active

b2: IR active

hence, there are 3 IR-active transitions → 3 IR bands

what is the overall selection rule of IR transitions

a vibration must have the same symmetry (species) as one of the x, y, or z

(i.e. must have a symmetry species matching the dipole moment operator)

what is the selection rule of a vibration being raman active for symmetry reasons?

for any process that involves the absorption of light, the transition is allowed, if and only if, the triple product contains the totally symmetric representation

Γgs = always totally symmetric ~ 1

Γes = Γvib = TREAT EACH VIBRATION SEPARATELY

Γ(a) = symmetry of the polarisability operator = sum of x², y², and z², xy, xz, yz representations in the point group

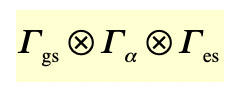
what is the difference in the selection rules for IR and raman activity?

IR activity = triple product w.r.t. symmetry of the dipole-moment operator

Raman activity = triple product w.r.t. symmetry of the polarisability operator

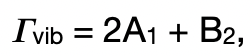
describe the raman-active transition in C2v

a1: raman active

b2: raman active

hence, there are 3 raman active transitions → 3 raman bands

what is the overall selection rule of raman transitions

a vibration must have the same symmetry (species) as one of the x², y², z², xy, xz, zy

(i.e. must have a symmetry species matching the polarisability operator)