Secants, Tangents, Limits, Continuity

secant

• average rate of change

• f(b) - f(a) / b - a

tangent

• instantaneous rate of change

• slope at a specific pt of graph

• f(a+h) - f(a)/h (as h approaches 0, therefore a very tiny interval)

a real limit only exists if

• it approaches a REAL, UNIQUE NUMBER

• both sides of value approaches the same number (right lim = left lim)

• even tho limits at infinity and negative infinity technically DNE, we still use them to get info about graph

get limits for restricted x values by

• testing how values very near the restricted value behave

• from both left and right side

• if it approaches a real number, there is likely a hole at the restricted value

• and factors on top and bottom can cancel out

if a restricted value of a fn has infinity limits, that means that graphically, there is a

vertical asymptote at the restricted lim (evaluated on both sides)

ceiling fn

output = the input rounded up

ex: input = 3.01, output = 4

input = 3, output = 3

input = 2.8, output = 3

input = 2.01, output = 3

the limit at 3 would not exist even though f(3) exists since the left and right side do not approach the same value

ways to evaluate limits

1. numerically (plug in nearby values)

2. graphically (studying the graph of fn)

3. using limit laws

4. using direct substitution (if the value is in the domain of the fn)

5. using algebraic tricks (cancelling out factors/manipulating fn to obtain a diff fn)

limit laws

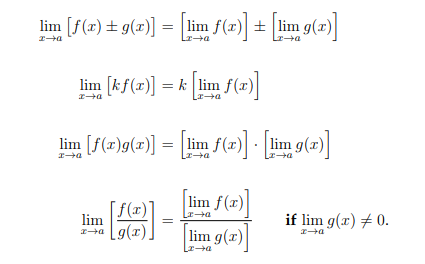
reasons why f could be discon at x = a

• a is not in the domain of f

• limit of x→a DNE

• limit of x→a exists but does not equal f(a)

on graphs, discontinuities happen at

holes, jumps, vertical asymptotes

if f and g are continuous at a, then the following functions are also continuous at a

the given functions are continuous at every real number IN THEIR DOMAINS

• poly

• rat fn

• root fn

• trig fn

• inv trig fn

• exp fn

• log fn

if you are taking the lim of a composition of fns at x → a, then you can move the lim to the inner fn PROVIDED THAT:

the outer fn is continuous

you can check that there’s a root in a certain interval PROVIDED THAT the interval is continuous on all x-vals in the interval by using INTERMEDIATE VALUE THEOREM

EX. on interval [1,2]

f(1) = 3

f(2) = -10

therefore, the fn must cross the x-axis at some pt meaning there is a root

to determine horizontal asymptotes

• take limit of fn at x → infy and x → -infy

• factor out the x with the highest degree

• directly substitute in the infy (NOTE: 1/infy is approx 0)

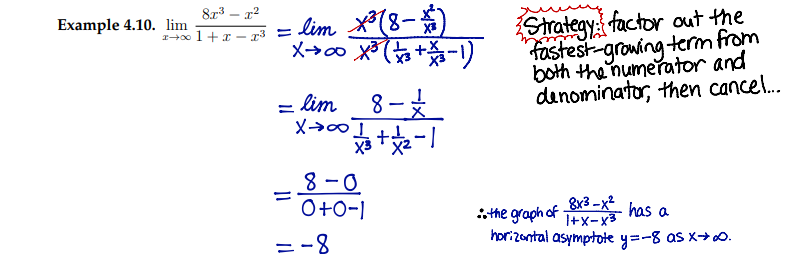
squeeze theorem example

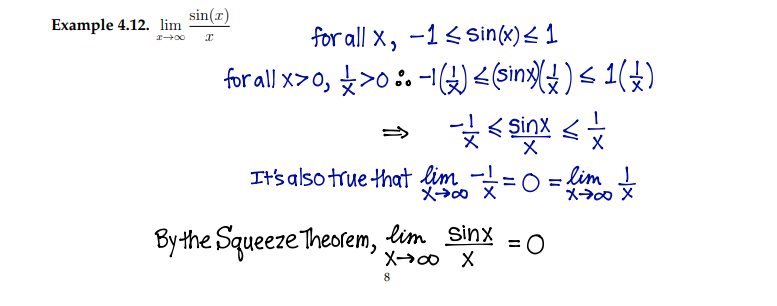
taking infy limit for absolute value fns

• if x → infy, then |x| = x

• if x → -infy, then |x| = -x