Reflection of light - Part 2

rules of sign conventions: distances ALONG the axis

distances are measure from the vertex A of the mirror

distances measured in the SAME direction that the light rays are travelling in - positive sign

distances measured in the OPPOSITE direction that the light rays are travelling in - negative sign

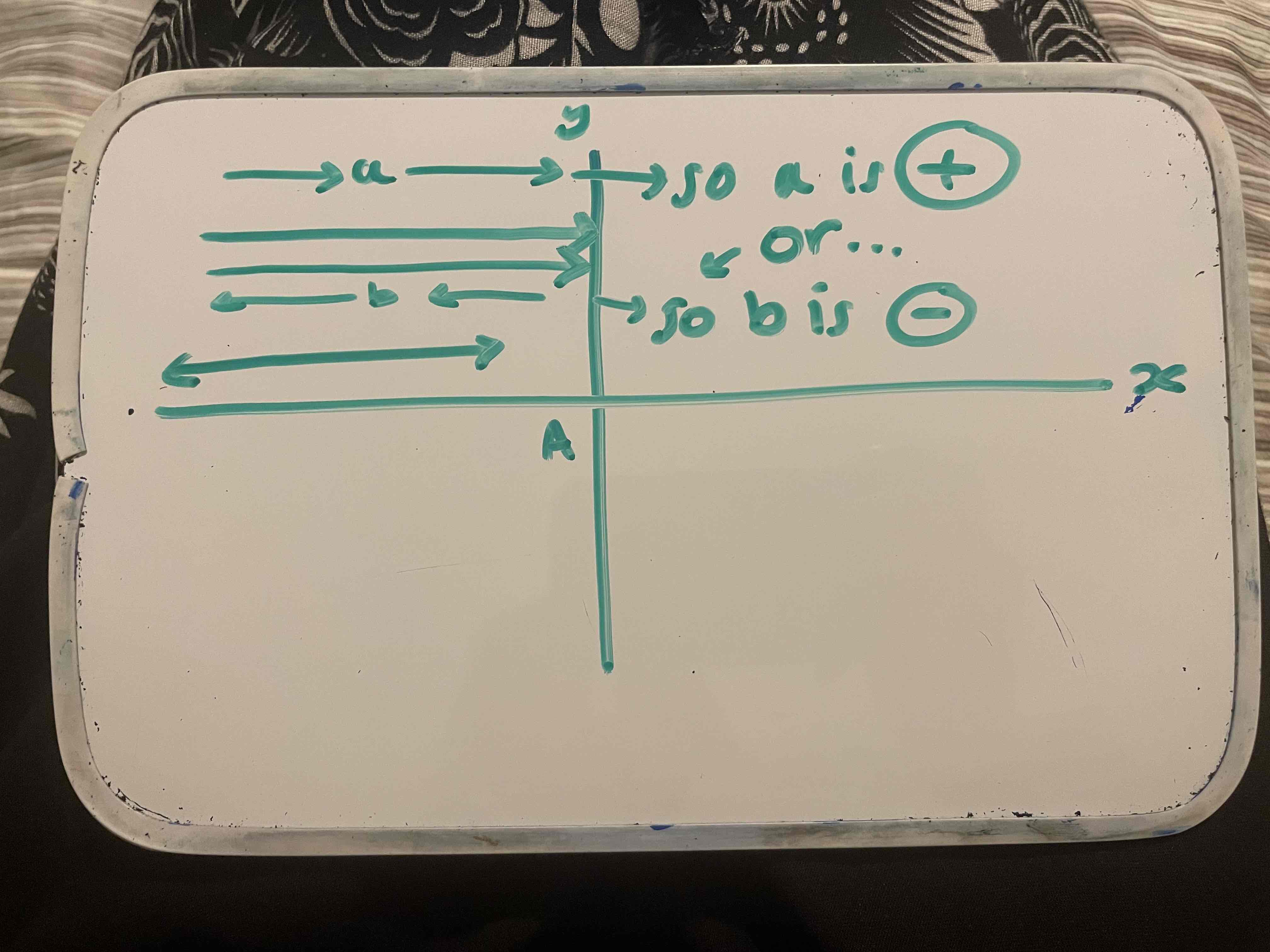
what does r represent

radius of curvature

what does f represent

focal length

what is the relationship between r and f in BOTH concave and convex mirrors

radius of curvature = 2 x focal length

r = 2f

or f = r / 2

purpose of spherical mirrors

change the direction of rays of light and to alter the curvature of the incident wave front

what does the formation of an image by a spherical mirror depend on

the type of mirror - concave or convex and the position of the object

the position, nature and size of the image depends on the above^^^

two methods to calculate the position and size of the image

1 - graphical construction method

2- analytical method

how are spherical mirrors represented in the graphical construction method

straight vertical line with the top indicating convex or concave

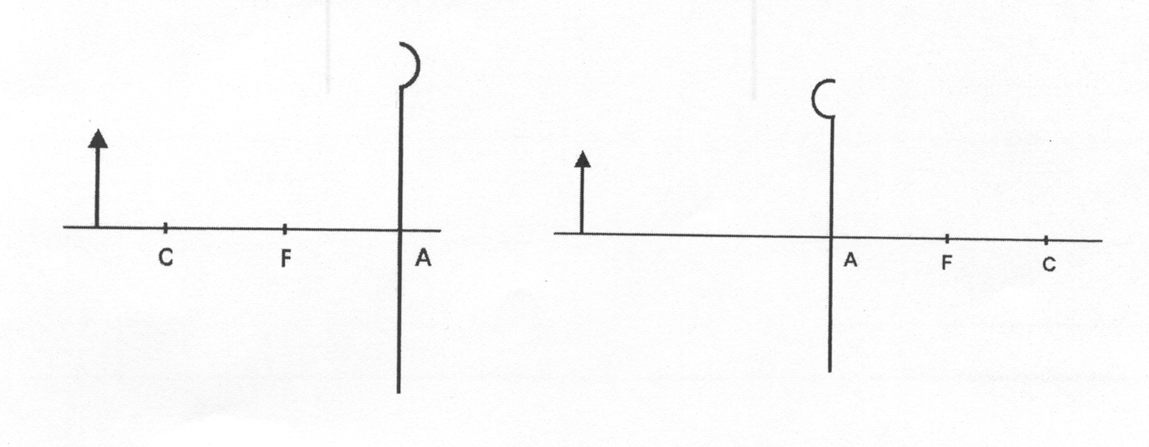
explain the components of a graphical construction diagram and what they are briefly

A = pole/vertex

C = center of curvature (AC = r)

F = focus (AF = f = r/2)

a scale drawing method which makes use of construction rays

these rays of light take a definite predictable paths following reflection

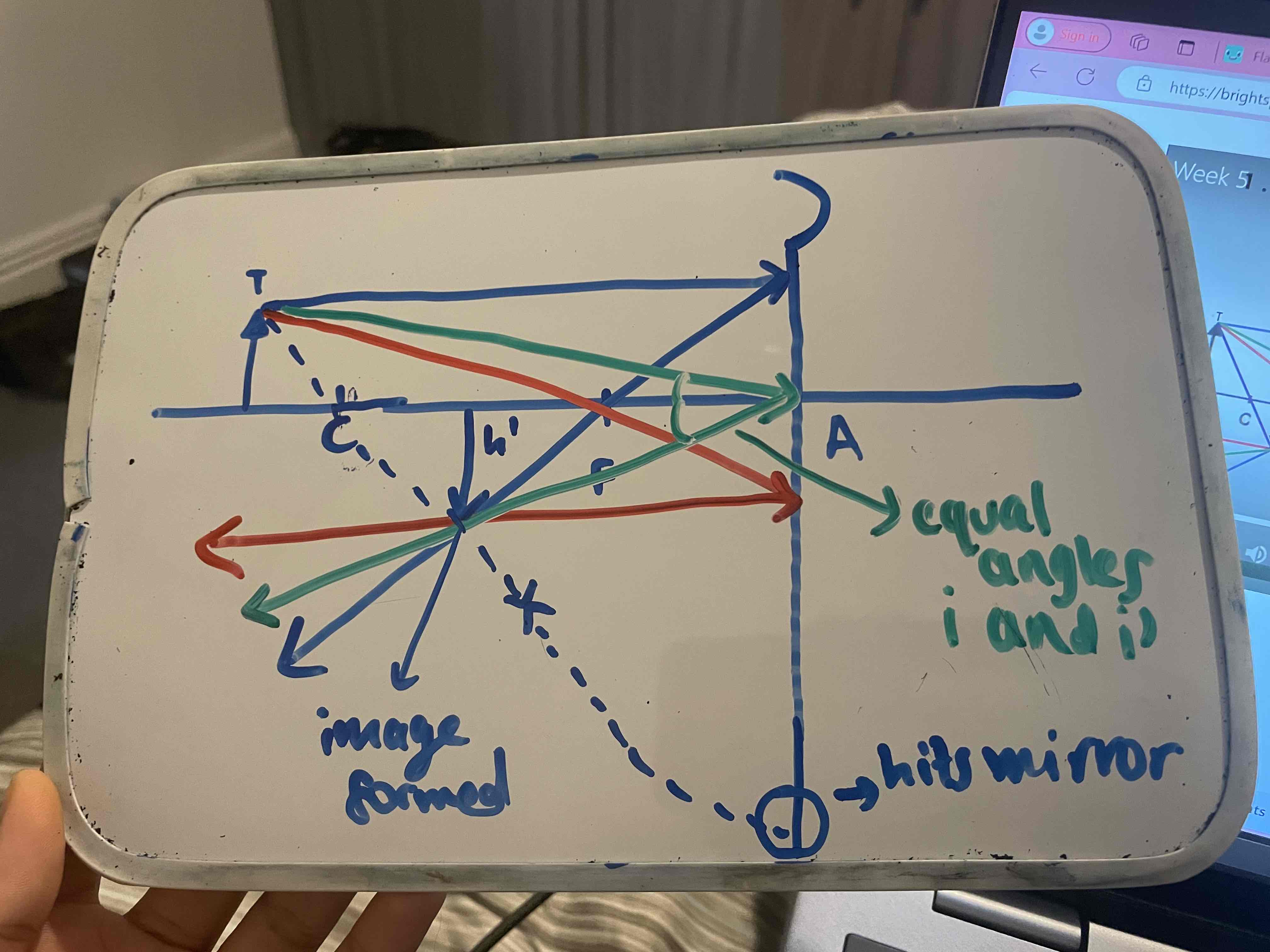
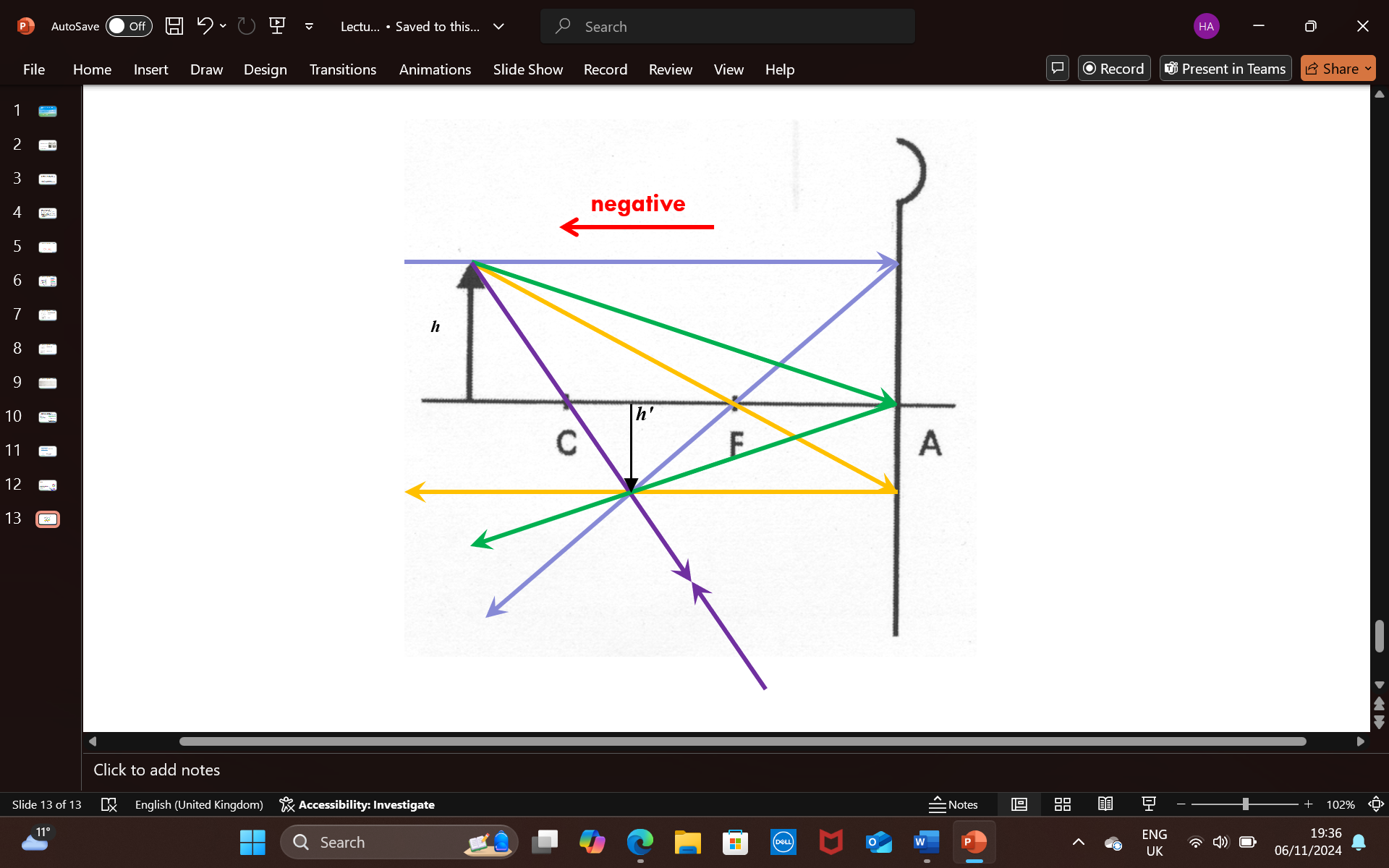
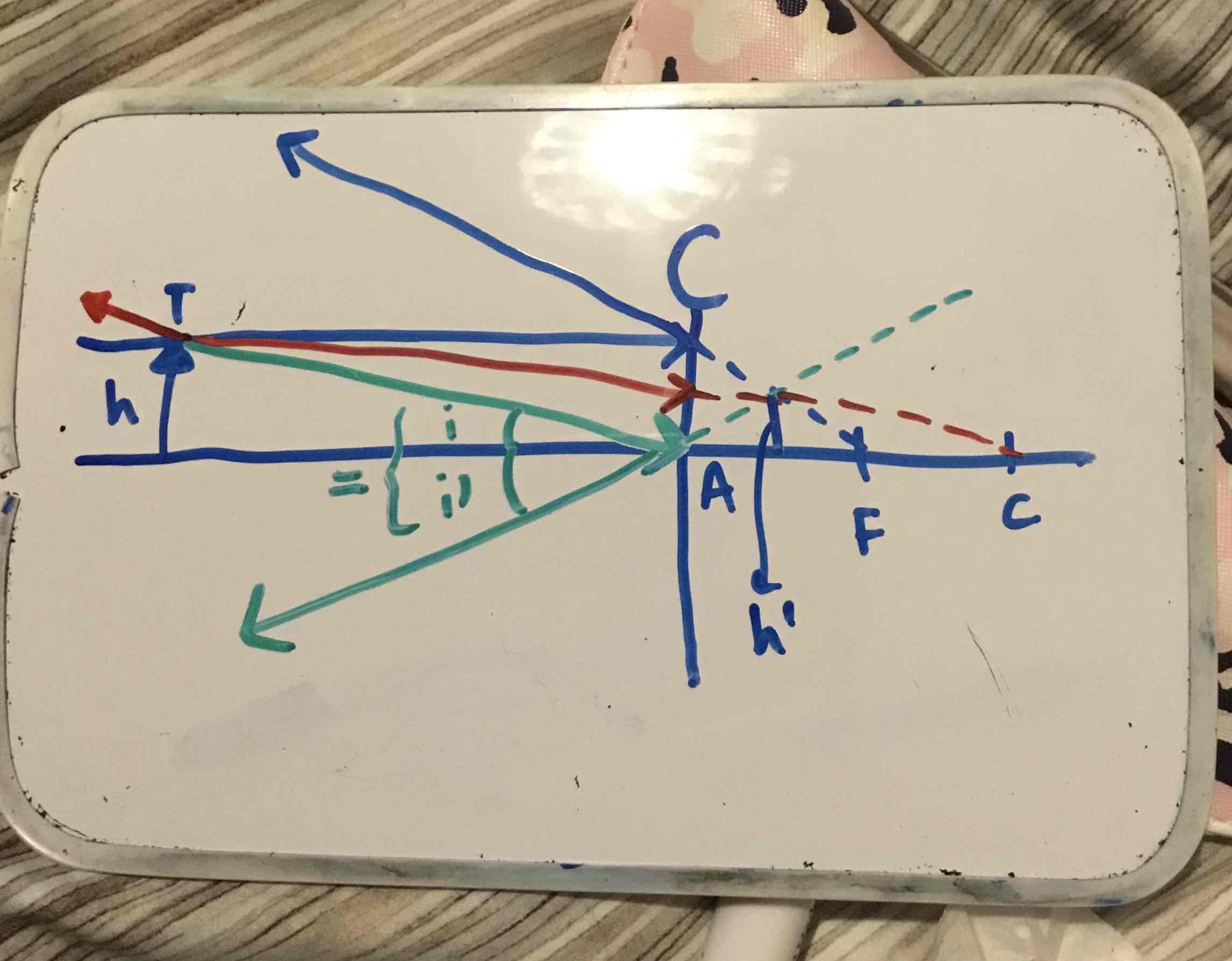
explain the path of light rays (4) in a graphical construction drawing to produce an image in a CONCAVE mirror

1- ray from T which is parallel to the principle axis hits the mirror and is reflected back through F

2- a ray from T passes through F and hits the mirror, after reflection it becomes parallel to the principle axis

3- a ray from T meets the vertex/pole (A) at some angle of incidence (i), and is reflected back at the same angle i, / law of reflection i = i’

4- a ray from T passes through C (center of curvature), strikes the mirror normally (in the periphery) and is reflected BACK along the same path

the point where all the rays intersect = where an image is formed ( a real and inverted image, slightly smaller than object)

h = height of object, so h’ = height of the image

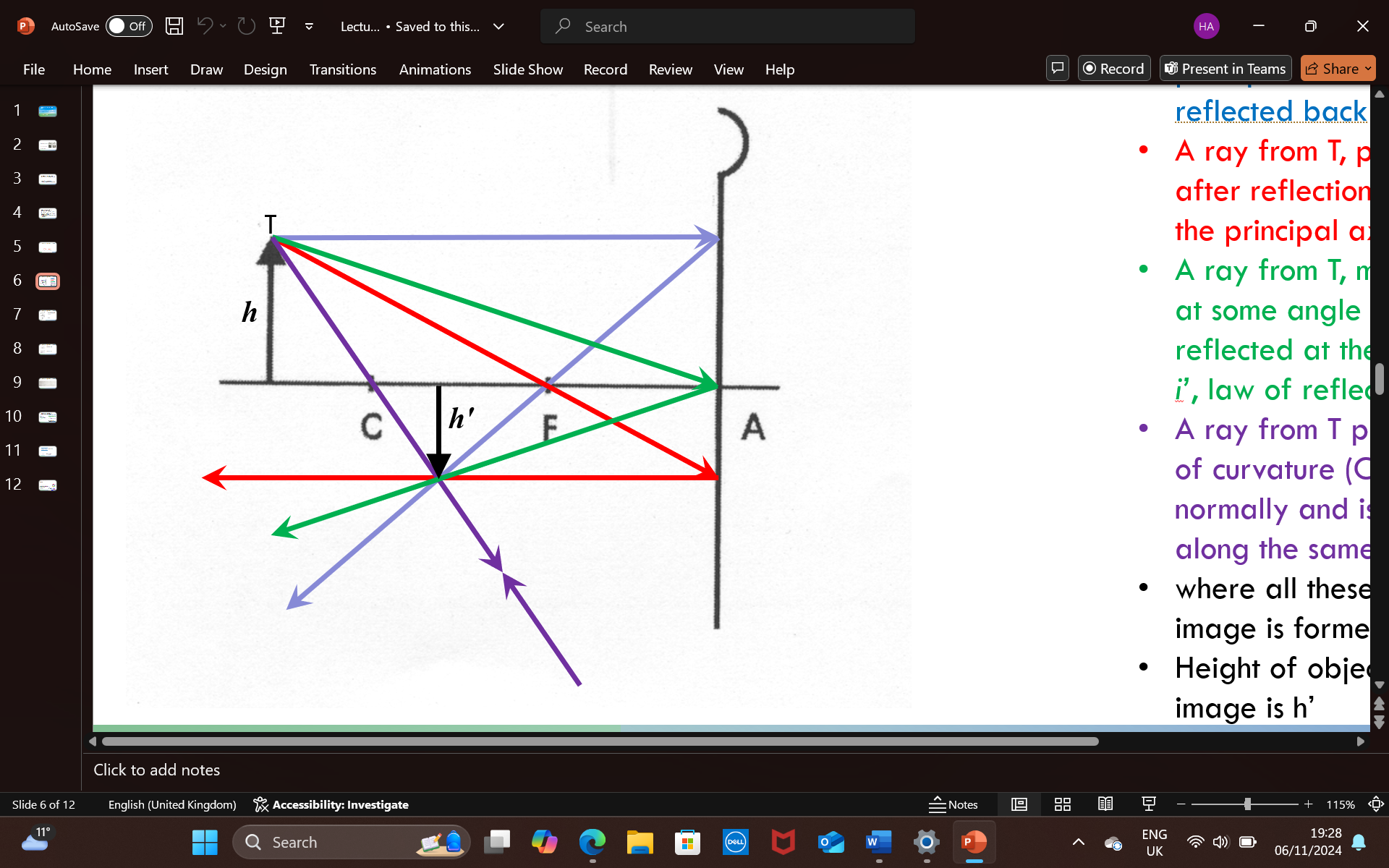
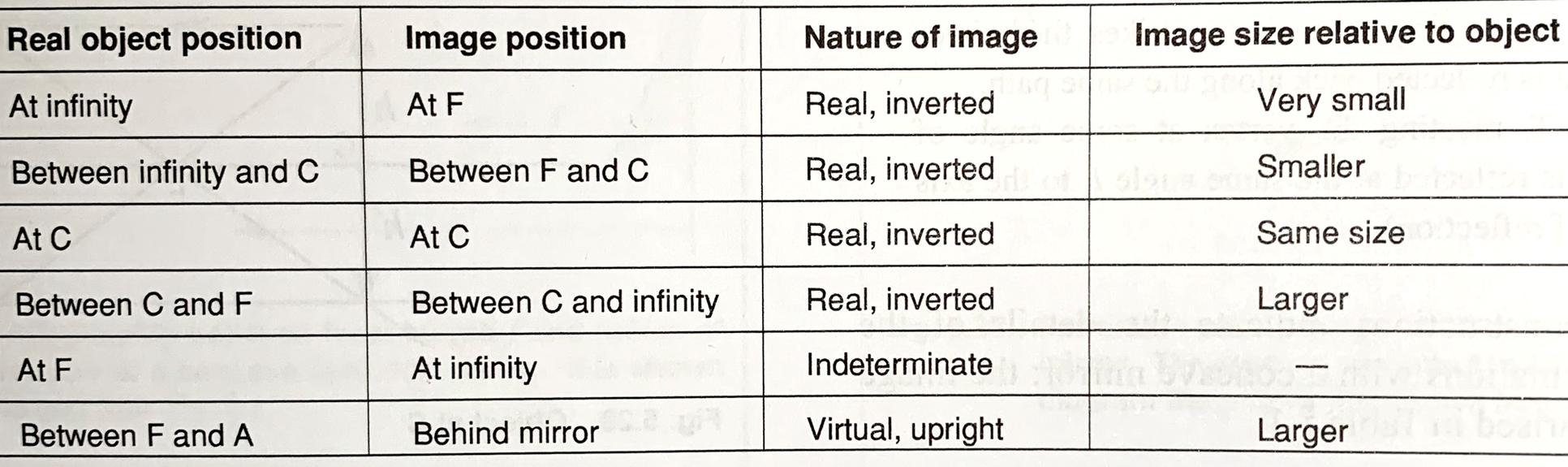
explain the different conditions in which we can use only 2 light rays from the object to find the position of the image formed (4)

1 - the object (h) is beyond/further away than C, and a real and inverted image is formed between F and C, the image is smaller than the object

2- the object (h) is at C, and a real inverted image is formed at C, the size of the image is the same as the size of the object, h = h’

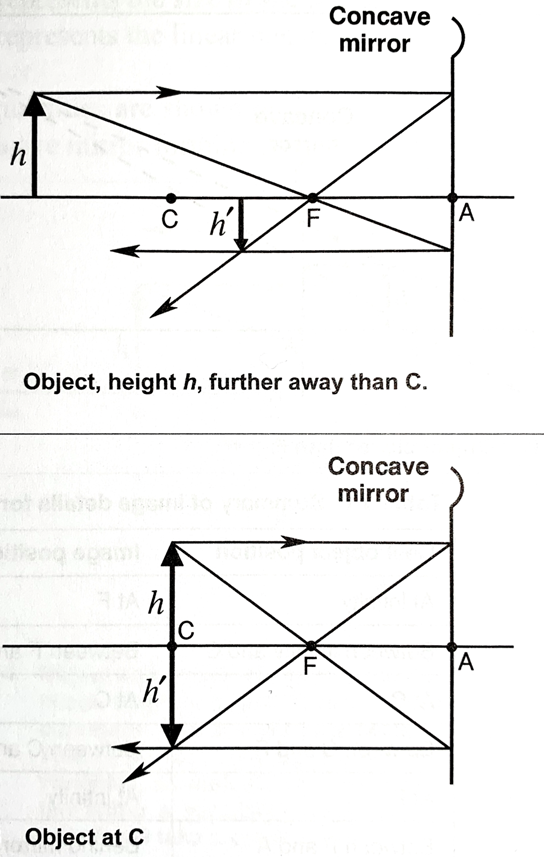
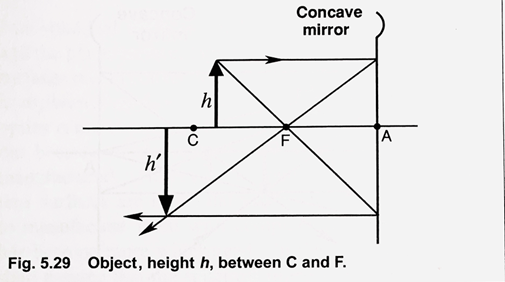
3- the object is between C and F, and a real inverted image is formed beyond C, the size of the image will be slightly bigger than the object

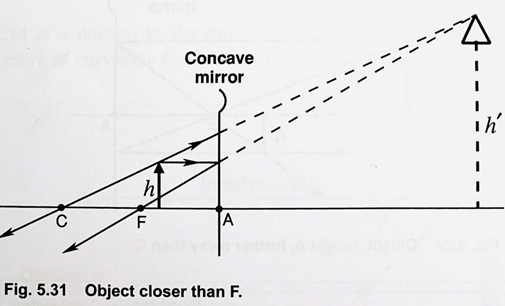
4- the object is between F and A, and a virtual upright image is formed behind the concave mirror, size of image is greatly larger than the object

the position of the object in relation to the position of the image formed and its nature and size in relation to the object at different points

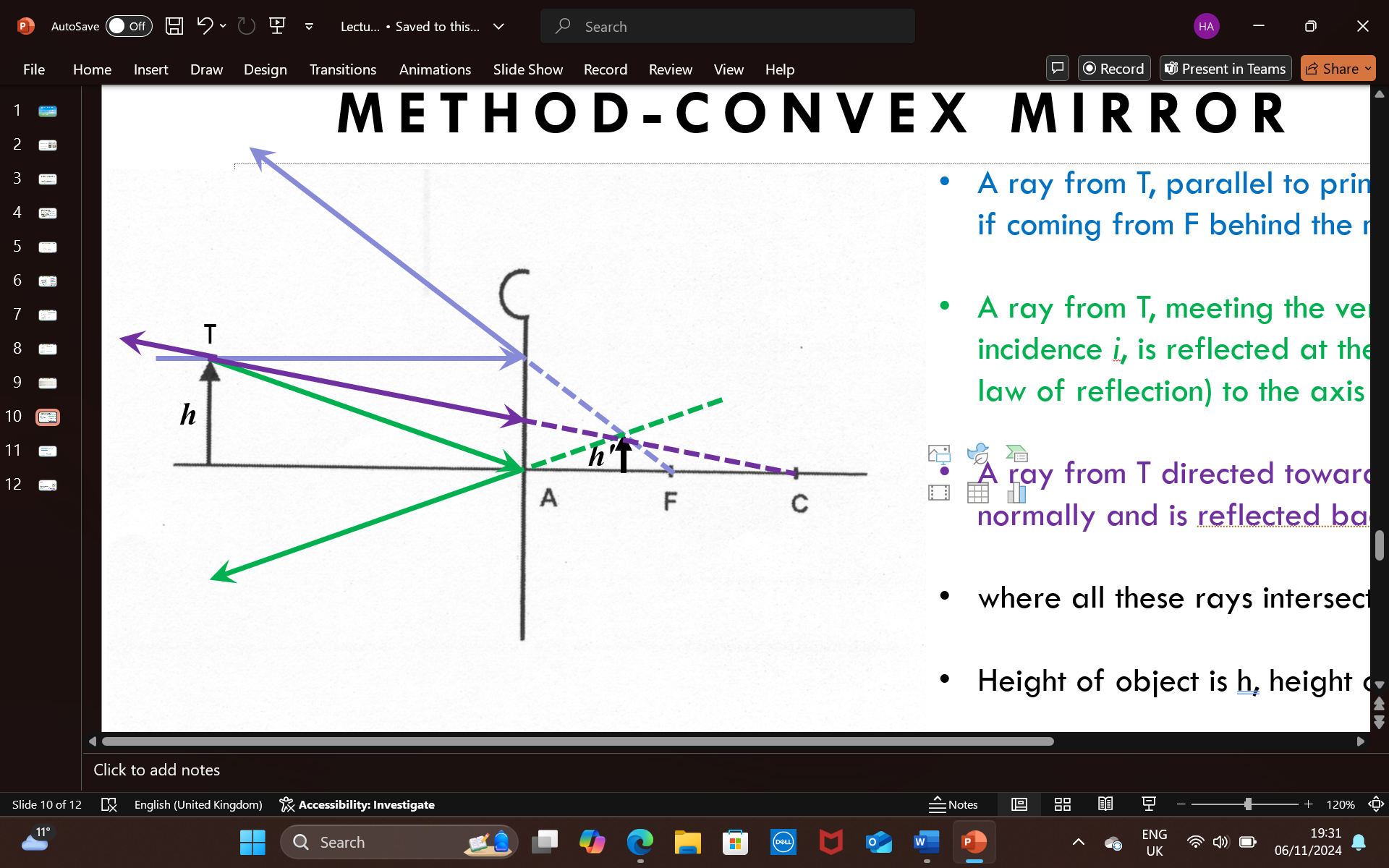
explain the path of light rays (3) in a graphical construction drawing to produce an image in a CONVEX mirror

1 - a ray from T, parallel to the principle axis is reflected as if it is coming from F behind the mirror

2- a ray from T meets the vertex/pole (A) at some angle of incidence (i), and is reflected at the same angle i’ (angle of i = angle of i’) to the axis

3- a ray from T directed towards C meets the convex mirror normally and is reflected back along the same path

where all the rays intersect = a virtual upright and (always) smaller image (than the object) is formed - irrespective of where the object is it will ALWAYS produce this kind of image ^^^

h = height of object and h’ = height of image

formula for the analytical method and each symbol (mirror formulae)

2 / r = 1 / f = 1 / l + 1 / l’

f - focal length of mirror

r - radius of curvature of the mirror

l - distance of the object from the mirror

l’ - distance of the image from the mirror

formula to calculate m (linear magnification)

m = - l’ / l = h’ / h

m = linear magnification

h = object height

h’ = image height

rules of sign conventions: distances (height) perpendicular (vertical) to the optical axis

all heights should be measured from the principle axis AC

a height measured above the axis is given a positive sign (+)

a height measured below the axis is given a negative sign (-)

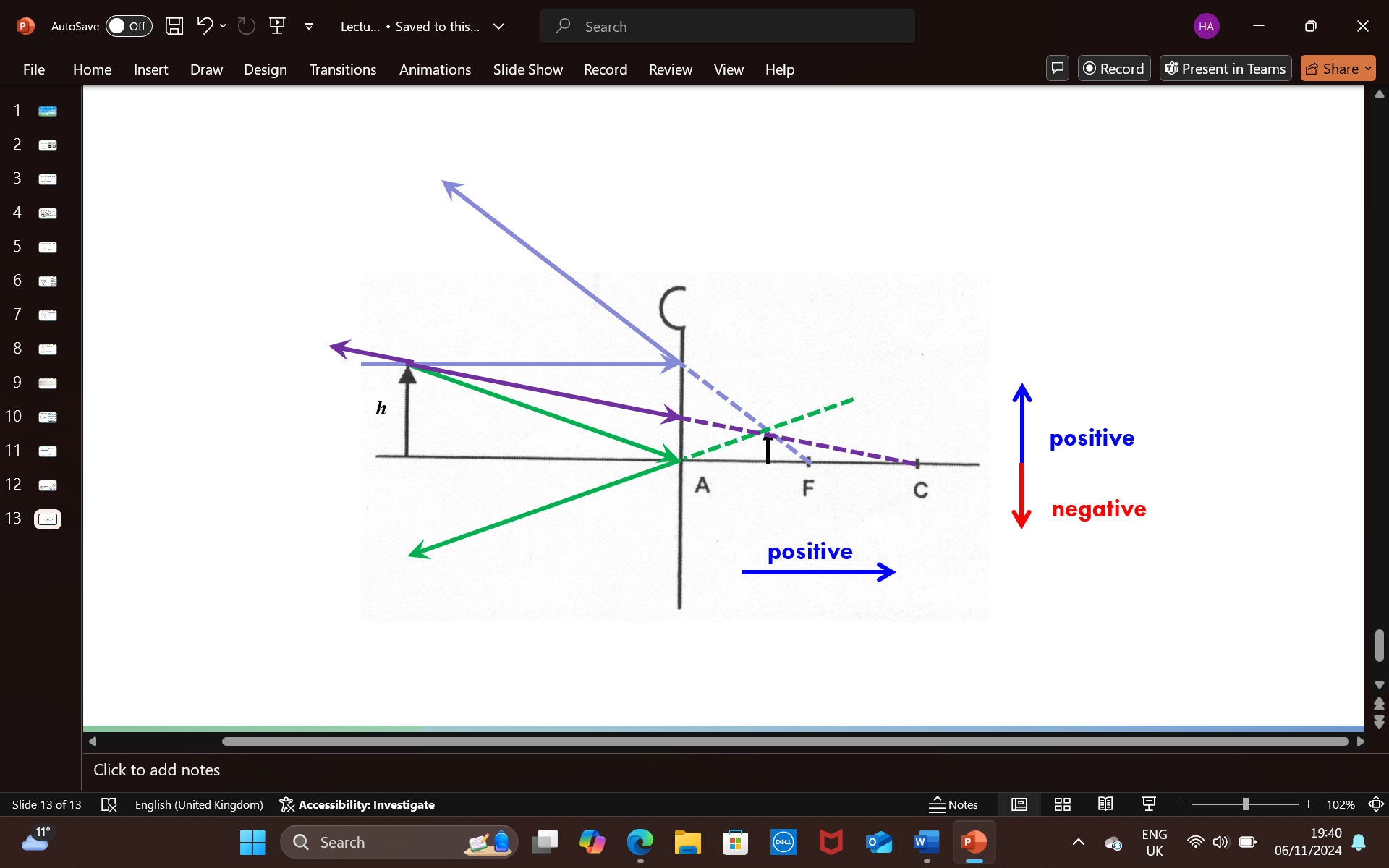
what are the signs of focal length and radius in concave and convex mirrors

concave: focal length and radius - negative values

convex: focal length and radius - positive values