Ap Calculus AB - Unit 3 Review
0.0(0)
0.0(0)
Card Sorting
1/9
Earn XP
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
10 Terms
1
New cards
chain rule
d/dx[f(x)gx)] = f’[g(x)]*g’(x)
![<p>d/dx[f(x)gx)] = f’[g(x)]*g’(x)</p>](https://knowt-user-attachments.s3.amazonaws.com/9225a5ed-c264-4607-bad7-353cf4a10609.png)
2
New cards
implicit differentiation
Take the derivative like normal except for anything except any variable that is not based on x, then take derivative in context of the variable. For example, d/dx(5y²) → 10y*dy/dx

3
New cards
Inverse derivatives
Function must be invertible and differentiable.
If f(x)=0, then the inverse function is differentiable, and the inverse of the derivative of the original function is equal to the derivative of the inverse function.
4
New cards
d/dx[arcsin(u)]
u’/sqrt(1-u²)
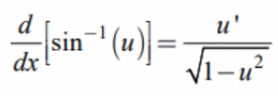
5
New cards
d/dx[arccos(u)]
-u’/sqrt(1-u²)
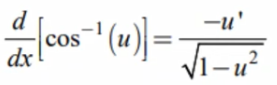
6
New cards
d/dx[arctan(u)]
u’/1-u²
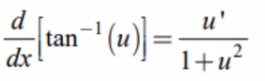
7
New cards
d/dx[arccot(u)]
-u’/1-u²
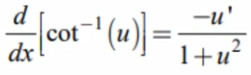
8
New cards
d/dx[arcsec(u)]
u’/[|u|sqrt(1-u²)]
![<p>u’/[|u|sqrt(1-u²)]</p>](https://knowt-user-attachments.s3.amazonaws.com/bddb7477-2f6a-4bf3-b148-c624fb4cf899.png)
9
New cards
d/dx[arccsc(u)]
u’/[|u|sqrt(1-u²)]-
![<p>u’/[|u|sqrt(1-u²)]-</p>](https://knowt-user-attachments.s3.amazonaws.com/ab189768-270b-4e70-a8df-d9593e41c244.png)
10
New cards
y’’
d²y/d²x