Topic 6: Sampling and Sampling Distribution

What is the purpose of statistical inference?

• obtain information about a population from information contained in a sample.

What is a population?

• set of all elements of interest.

What is a sample?

• subset of the population —> e.g. S&P 500 or the FTSE 100 indices are sample of stocks.

What is one advantage and one disadvantage of sampling from population?

• easier and more efficient.

• It is sometimes very costly or simply not possible

Why random sampling?

• to avoid biases

• allows us to use probability to make inferences about unknown population parameters (such as mean and variance)

What is point estimation?

• used to estimate an unknown valued (called a population parameter) by using a single number calculated from sample data.

What does point estimator mean?

• the statistic used to estimate a population parameter. We refer to:

• x as the point estimator of the population mean µ.

• SX as the point estimator of the population standard deviation σ.

• pˆ as the point estimator of the population proportion p.

What is the point estimate?

• The numerical value we get when apply the estimator to the actual sample data.

What is the estimation error?

• difference between the point estimate and the true

  population parameter we are trying to estimate.

When a point estimator equals the population parameter

• point estimator is unbiased.

What is a sampling error?

• result of basing an inference on a random sample

  rather than on the entire population.

Formulas for calculating sample mean, SD & proportion

Sample mean value of random variables is defined as:

What are the expected value and variance of sample mean?

What happens if the sample size, n, isn’t a small fraction of the population size, N?

• the individual sample members are not distributed independently of one another.

• observations are not selected independently.

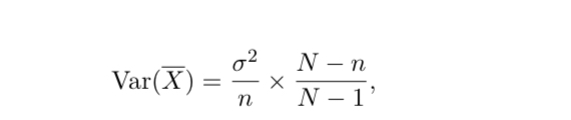
What is this term called? (N-n)/(N-1)

finite population correction factor.

What does the Central Limit Theorem (CLT) state?

• the mean of a random sample, will be approximately normally distributed with mean µ and variance σ2/n, given a large-enough sample size.

What does the law of large numbers conclude?

• given a random sample of size n from a population, the sample mean will approach the population mean as the same size n becomes large

Formula for sample proportion

What does a high variance for a process imply?

• wider range of possible values