Week 1 - Function Operations, Graph Transformations

What is the formula to find the slope of a line from two points? How do you know based on the slope if a linear function is increasing, decreasing, or constant? How do you know if a slope is infinite? Based on the slope, how do you know if the line is a function or not? How can you find the horizontal and vertical line?

consider the line: ax+by=c

• if b=0, the slope is infinite/undefined

(x1,y1) (x2,y2)

slope (m) = (y2-y1)/(x2-x1)

m>0 → linear function is increasing

m<0 → linear function decreasing

m=0→constant

if the slope is undefined, the line is not a function

a=0, y=# (horizontal line)

b=0, x=# (vertical line)

What is the standard equation of a line? When is it a horizontal or vertical line? How do you find it from the equation?

ax+by=c

• a, b, c are constants

• a=0 → solve for y, you get y=k, a horizontal line

• b=0 → solve for x, you get x=h, a vertical line

point-form slope equation

y-y1=m(x-x1)

Slope-intercept form

y=mx+k

When do you know if two lines are parallel?

• the slopes of the two lines are equal

• OR

• the two lines are both vertical

When do you know if two lines are perpendicular?

if one is a vertical line and the other is horizontal

OR

if their slopes are negative reciprocals. That is, if one line has slope m1 and the other has slope m2 then m1 = −1/m2, (and also m2 = −1/m1)

When a question asks, “express the function as a piecewise defined function”, what does it mean?

Write the equations and inequalities for the piecewise function (don’t graph, they’ll already give it to you)

What is the difference quotient formula?

Difference quotient formula:

[f(x+h)-f(x)]/h

• slope of secant line

(f±g)(x)=?

(fg)(x)=?

(f/g)(x)=?

(it’s like the f of things)

(f+g)(x)= f(x)+g(x)

(f-g)(x)=f(x)-g(x)

(fg)(x)= f(x) times g(x)

(f/g)(x)= [f(x)/g(x)], given that g(x)≠0

What are the requirements for 2 functions to be equal?

1. they both have the exact same “rule” (equation)

   • ex) f(x) = x² and g(x) = x²

2. their domains are exactly the same

(f∘g)(x)=?

(f∘g)(x)= f(g(x))

How do you find the domain of a composite function? ex) f ◦ g , where f(x)=x²+2 and g(x)=sqrt(7-x)

1. find the domain of the function inside only (in this example, g(x))

2. insert g(x) into f(x), then find the domain

3. take the two domains and combine them

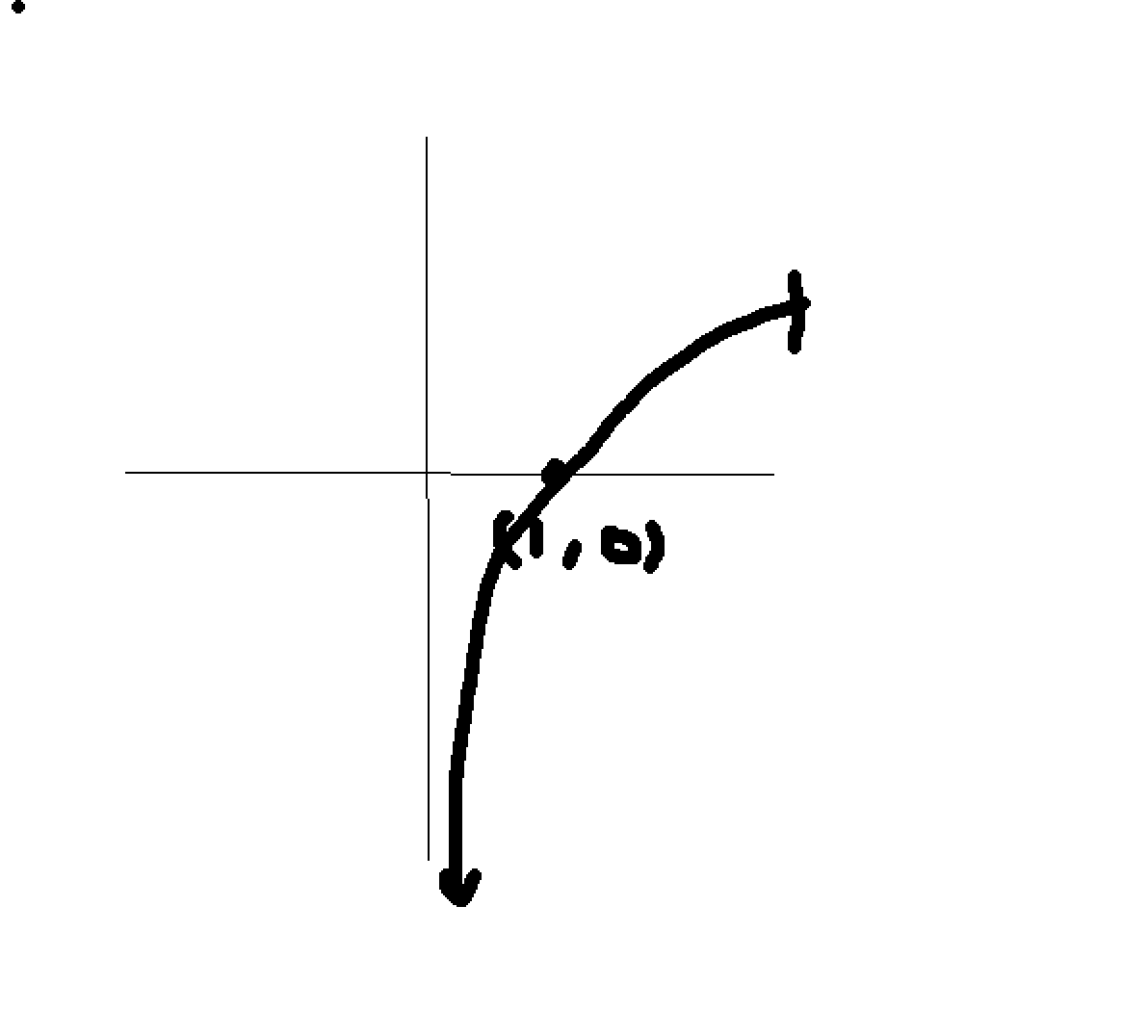
Generally, what does a reflection across the x axis vs y axis look like? How is it written in a function?

f(-x) → reflected across y axis

-f(x) → reflected across x axis

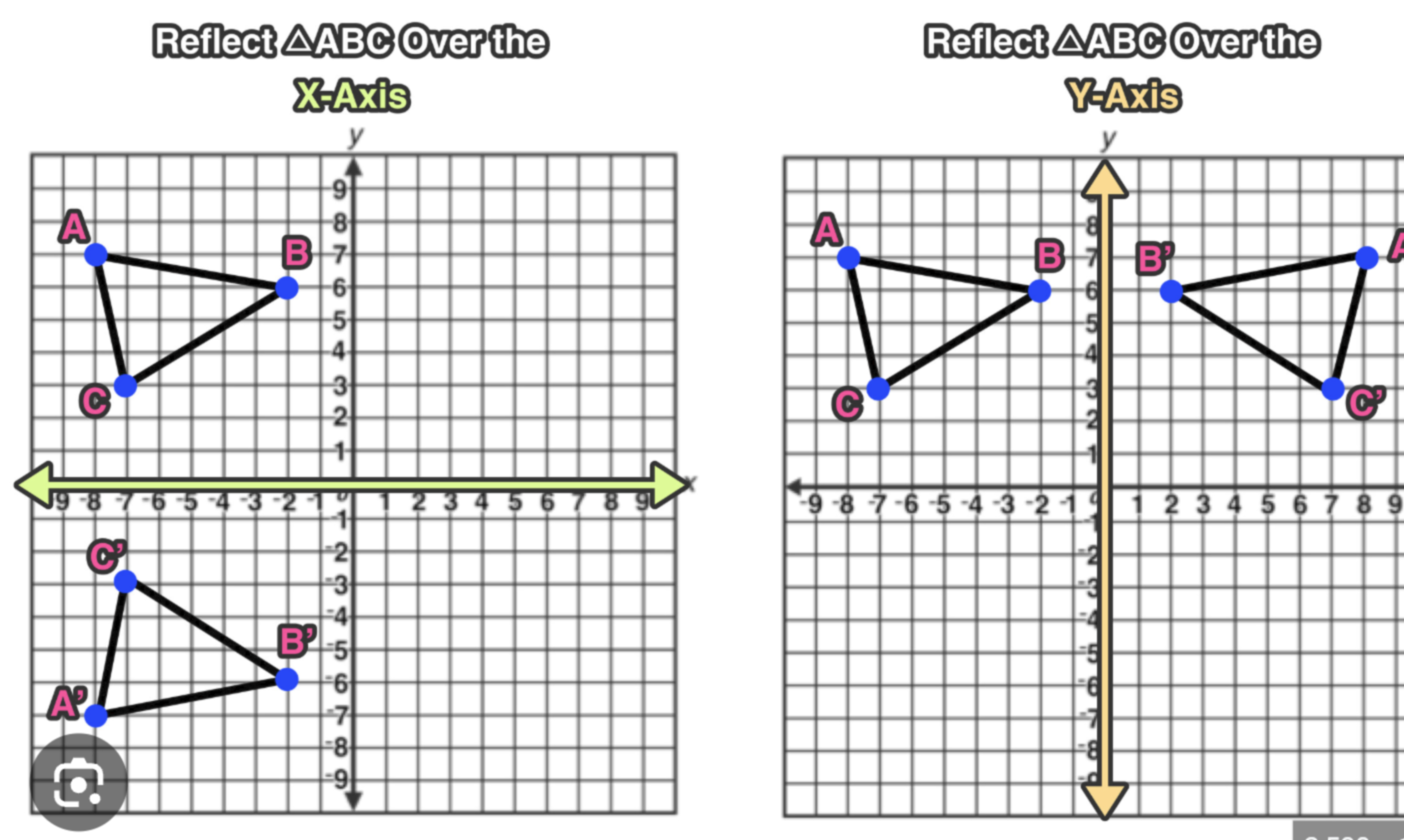
How does the “C” in the f(Cx) function transform the graph?

Given that “C” is positive:

• 0<C<1 (less than one, greater than 0) → horizontal stretch by 1/C

• C>1 → horizontal shrink by C

If “C” is negative:

• reflects across y-axis

WHEN GRAPHING: Multiply x-value you plug in by C

How does the “C” in the C⋅f(x) function transform the graph?

Given that “C” is positive:

• vertical shrink by C if 0<C<1 (less than 1, greater than 0)

• vertical stretch by C if C>1

if “C” is negative:

• reflect across x-axis

WHEN GRAPHING: Multiply output by C

Rules for the order of function transformations?

• horizontal and vertical transformations can be performed independent of order

• scale/reflection first, shift performed second, ALWAYS

  • shift: moves graph up/down, left/right

  • scale: shrink/stretch

• af(b(x+c))+d

  • a →scaling

  • b→scaling

  • c→shifting

  • d→shifting

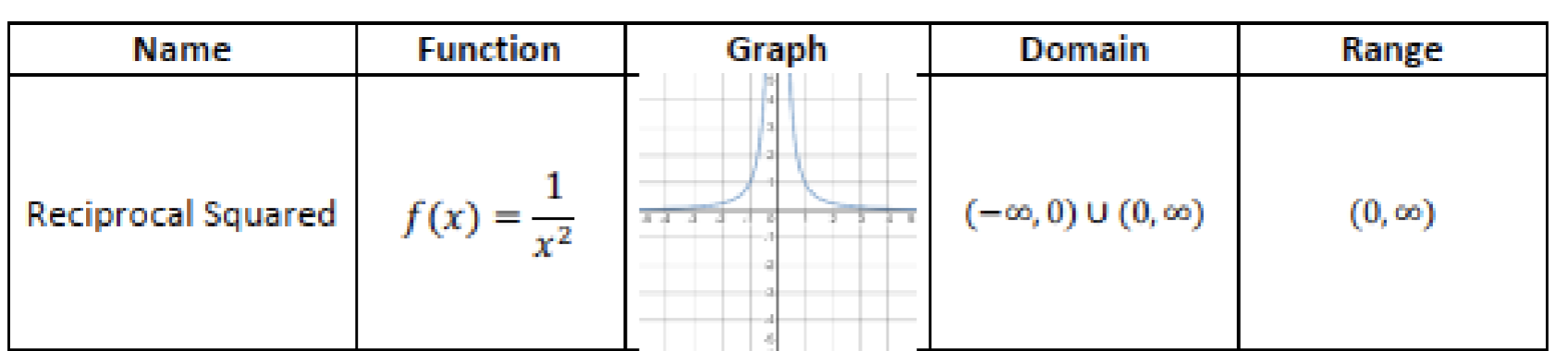
Write the function, graph, domain, and range for: reciprocal squared

image

Write the function, graph, domain, and range for: square root

image

Write the function, graph, domain, and range for: cube root

image

Write the function, graphing version of a function, transformation rules, cases, graph, domain, and range for: exponential

image

transformation rules: https://docs.google.com/document/d/12B4NOW8BjJUYy007wSQhJa-242vPO9xQntQj6jNaBAg/edit?tab=t.0

1. exponential

   • f(x)=ab^x

   • a→initial value

   • b→base, b>0 and b can’t equal 1

   • horizontal asymptote y=0

2. power

   • f(x)=ax^n

   • a→constant coefficient

   • n→exponent

   • 3 cases for power:

     • case 1: n is a positive integer

       • domain: all real numbers

       • if n is an even number → even function, range is [0, ∞)

       • if n is an odd number → odd function, range is all real numbers

       • no asymptotes

     • case 2: n is a negative integer

       • domain: (-∞, 0) U (0, ∞)

       • if n is an even number → range is (0, ∞)

       • if n is an odd number→ range is (-∞,0) U (0, ∞)

       • asymptotes: y=0 (horizontal), x=0 (vertical)

       • you cannot determine even/odd function based on n, you need to do the equation check

     • case 3: if n is a fraction (ex. x^1/n) or root (index n sqrt[x]) and n is a positive integer

       • you cannot determine even/odd function based on n, you need to do the equation check

       • n is an even number → domain and range: [0,∞)

       • n is an odd number → domain and range is all real numbers

Write the function, graph, domain, rules, and range for: logarithmic

image

(domain on left, range on right)

• f(x)=logᵦ(x)

• inverses of exponential functions

• ᵦ is the base, ᵦ>0 and ᵦ can’t equal 1

• x>0

Write the function, graph, domain, and range for: logistic

image

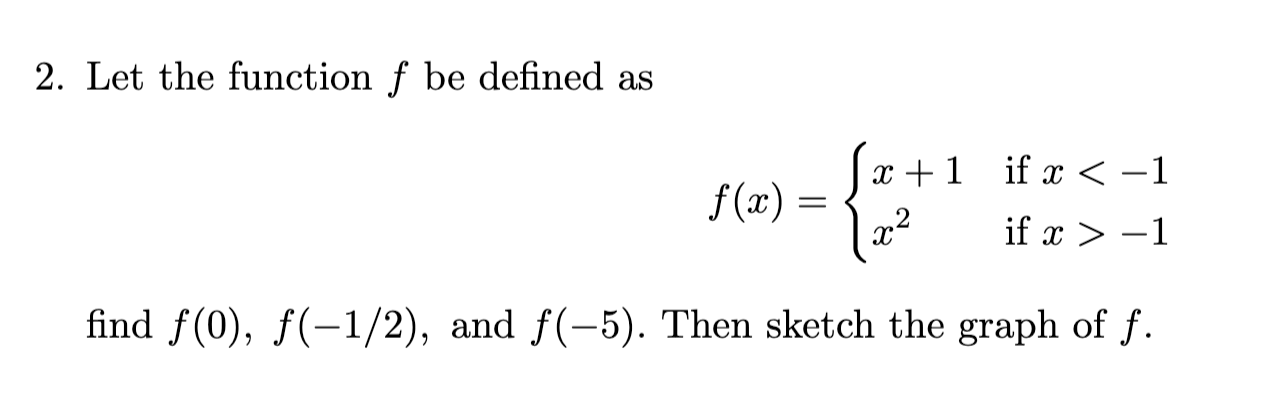
Practice problem

image

ignore the answers, just graph piecewise functions based on the inequality

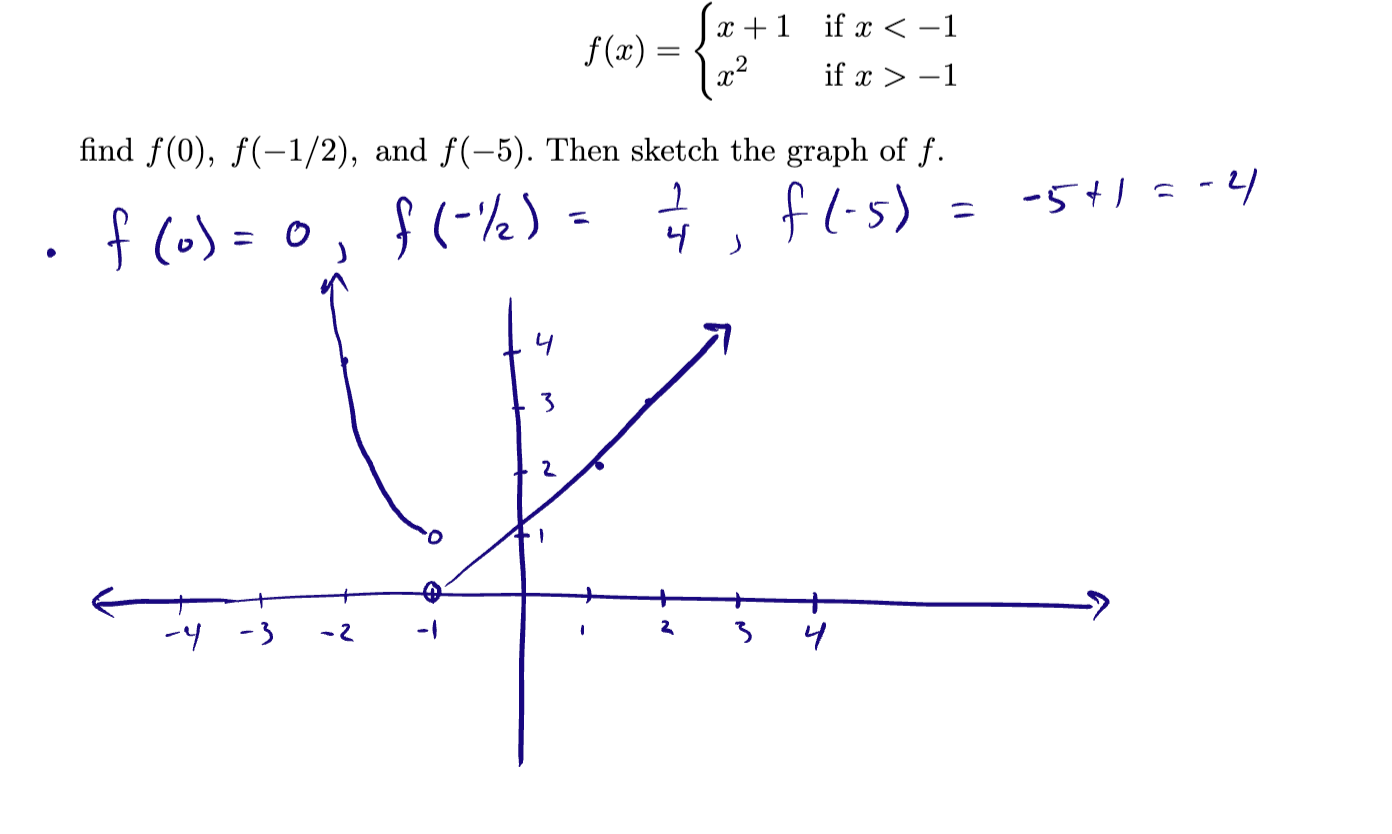
What does A∩B mean?

What does A∪B mean?

How do you solve them?

∩→ intersection (which elements are common to both sets?)

• ex) A={2,4,5,6,9} B={2,3,5,6,7,9,10}

• A and B have 2,5,6,9 in common

• so, A∩B={2,5,6,9}

  • write from lowest to highest number

• if there are no numbers in common, write ∅

∪→union (write all numbers in both sets, but only once)

• ex) A={1,2,3,4} B={3,4,5,6}

• A∪B={1,2,3,4,5,6}

• if one set has no numbers, just write all the numbers in one set

  • ex) X={2,5,8,12} Y=∅

  • X∪Y={2,5,8,12}

How do you find the domain for these functions?

1. polynomial only (no fractions or square roots)

2. fraction only (no square roots)

3. square root only (no fractions)

4. square root on the denominator

5. square root on the numerator

1. polynomial only (no fractions or square roots) → all real numbers

   • ex) 2x+1, 2x²+3x+1

2. fraction only (no square roots) → set denom ≠ 0

   • ex) (2x+1)/(x²+5x+6)

3. square root only (no fractions) → set ≥ 0

   • ex) sqrt(x+1)

4. square root on the denominator → set denominator > 0

5. square root on the numerator → set denom ≠ 0, set num ≥ 0, then take the intersection

   • ex of #5 In image

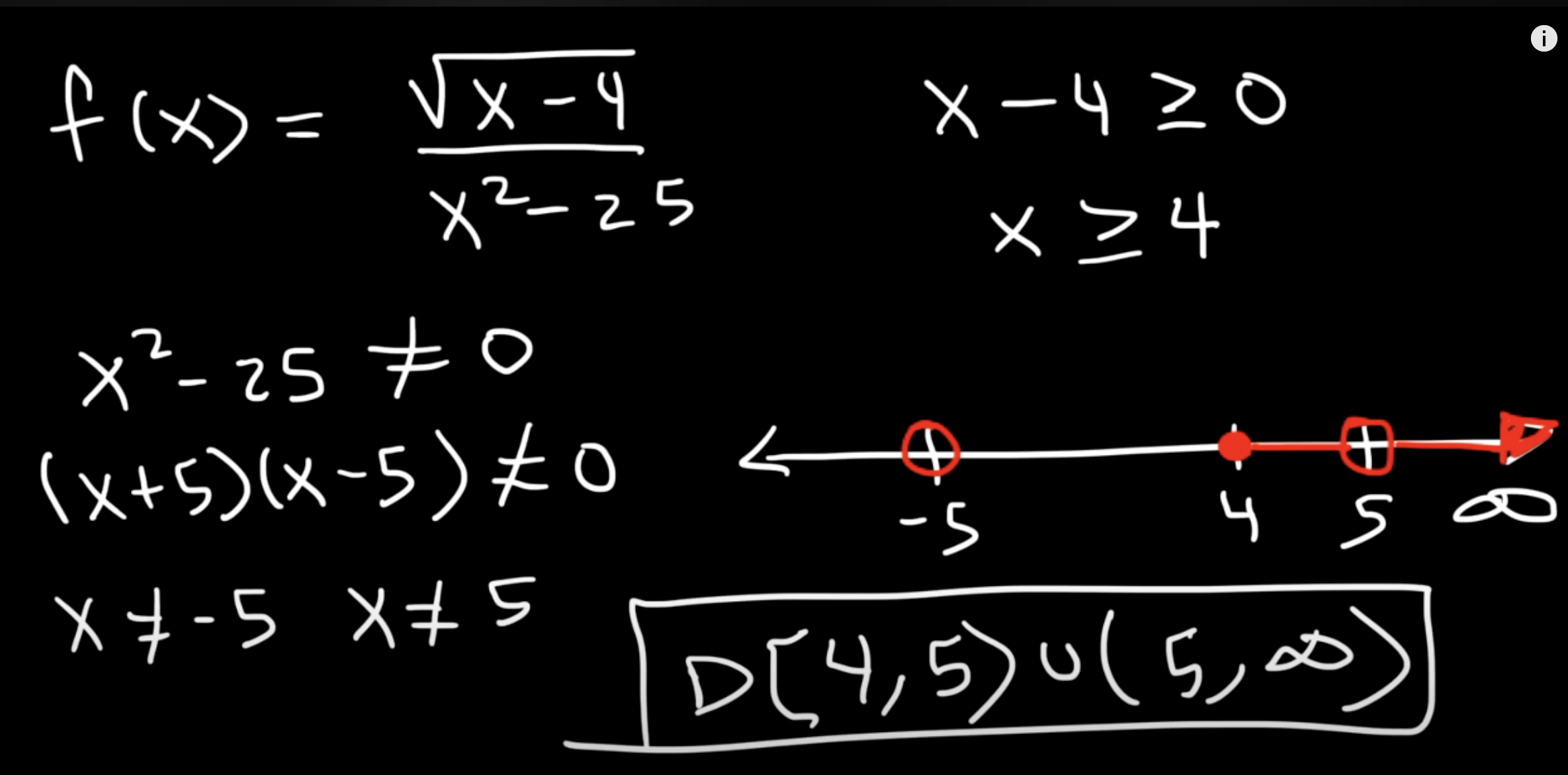
How do you write piecewise functions?

• see if there are any splits/pieces in the graph

• write f(x) { if (equation of first piece), (inequality for first piece), and so on

How to determine if a function is even, odd, or neither?

even: f(-x)=f(x)

odd: f(-x)= -f(x)

neither: f(-x) ≠ -f(x)

write pascal’s triangle, explain how to solve with pascal’s triangle ex) (2+h)^4

basically each number on the triangle is a coefficient, so for a go reverse from 4, b go forward from 0, and multiply each by the coefficient

link to pascal’s triangle: https://docs.google.com/document/d/1ATlltGHH9pqoVPXBgWqnAlX9YU6mEEpV-OcPuQmSXkY/edit?tab=t.0

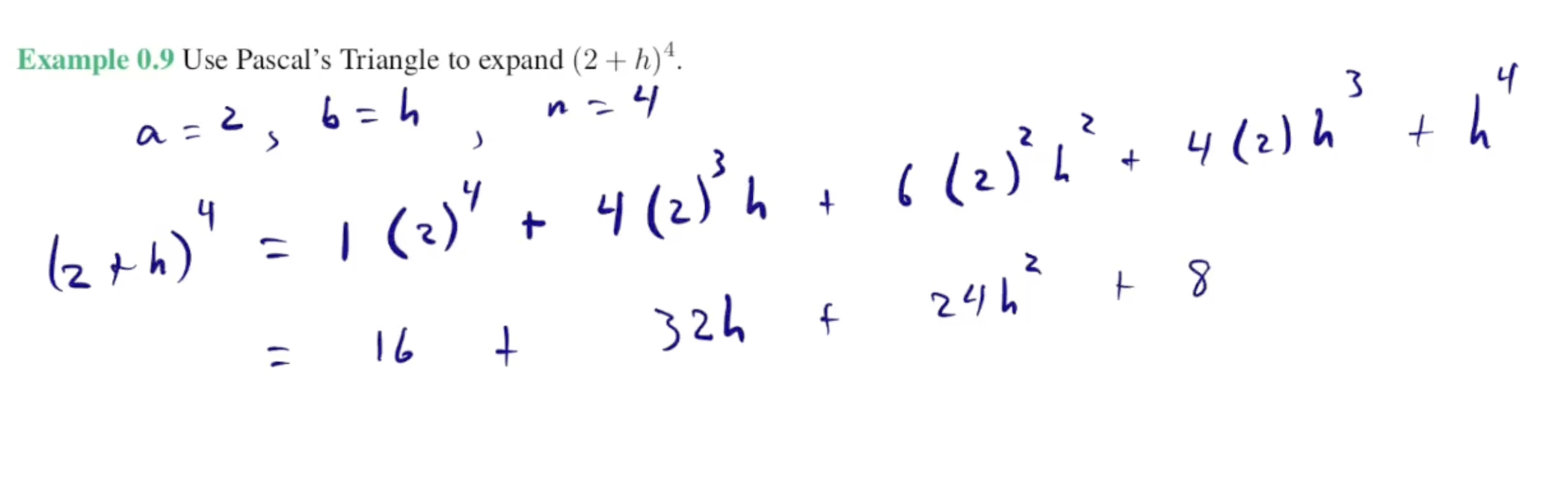
what is the degree of a polynomial?

degree of a polynomial is the largest exponent (ignoring the one with 0 as a coefficient)

rational (rules: what is it, what is its equation, what is the rule for the denominator?)

1. rational (fraction of two polynomials)

   • f(x)=P(x)/Q(x) (both are polynomials)

   • denominator can’t equal 0

   • polynomials (all polynomials are rational functions)

algebraic

1. algebraic

   • rational and polynomial functions

How do you determine if an equation is a function (algebraically)

1. make equation y= (if necessary)

2. determine if the y= equation you found is a function or not

n/a

n/a

How do you turn a quadratic function into graphing form?

Complete the square (ex. y=x²+4x+0)

steps

1. put the number without the variable on the opposite side of the equation

   • x²+4x=0

2. divide all numbers by the coefficient of the leading exponent

   • x²/1 +4x/1 = 0/1

   • x²+4x=0

3. add a mystery number to both sides (it is the coefficient of the second largest variable/2 squared)

   • x²+4x+(4/2)²=0+(4/2)²

   • x²+4x+4=4

4. now factor the side with the variables, then move the non-variable number to the same side as your variables

   • (x+2)²=4

   • (x+2)²-4

5. then you have your graphing form

   • (y,k)=(-2,-4)

How does f(-x) change the graph? how does -f(x) change the graph

f(-x) → reflect about y-axis

-f(x) → reflect about x-axis

How do you solve a²-b²?

Difference of squares: (a-b)(a+b)

How do you solve (a±b)^n?

Pascal’s triangle

How do you solve a^n-b^n?

Difference of powers: (a-b)(a^n-1 b^0+a^n-2 b^1…a^n-n b^?)

Quadratic formula

x=-b±sqrt(b²-4ac)/2a

How do you solve a³±b³?

Difference of cubes: (a-b)(a²+ab+b²)

sum of cubes: (a+b)(a²-ab-b²)

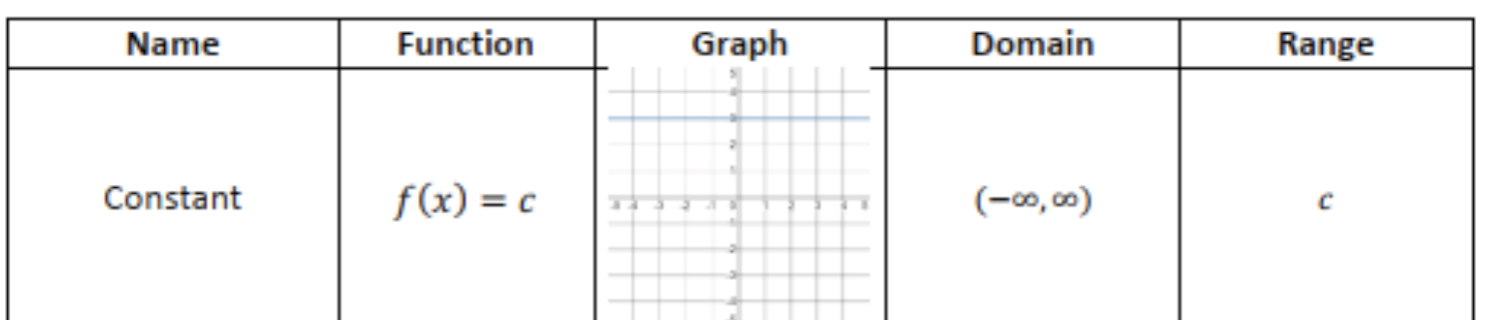
function, graph, domain, and range for: constant

image

function, graph, domain, and range for: identity

image

function, graph, domain, and range for: absolute value

image

function, graph, domain, and range for: quadratic

image

function, graph, domain, and range for: cubic

image

function, graph, domain, and range for: reciprocal

image

Draw the parent graph of ln(x)

image