9-Phase Equilibria of Mixtures

pressure vs mole chart

Gibbs Phase Rule F=2-pi+N

. =4-pi for 2 components

how many intensive properties F can be chosen

pi-# of phases

N-# of chemical species

F=4-pi in one phase =3

P,T,x defines the system in one phase

for VLE, pi=2 F=2

so T,x or P,x defines the system

for a given P,x

there is a temperature that gives two phases

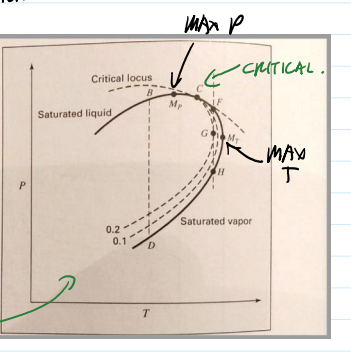
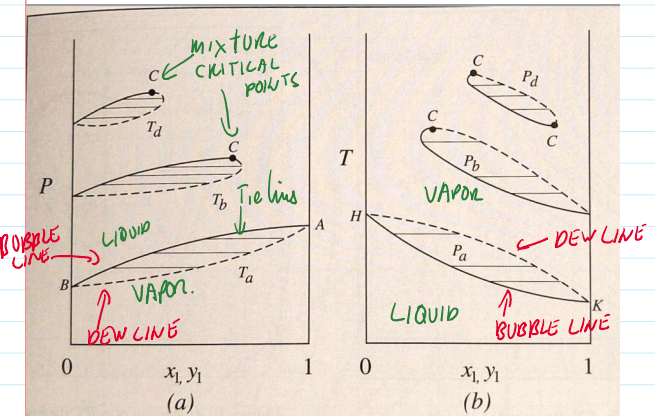
P,T graph varying composition

B—>D evaporation

F—>G—>H F: vapor condenses to a two phase mixtures through G, then vaporizes again (retrograde vaporization)

in a gas well, as we remove gas lower pressure

liquid can form. need to repressurize the well

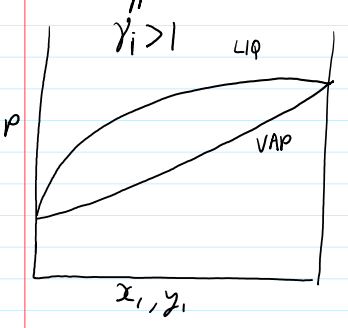
non ideal P-graph γi > 1

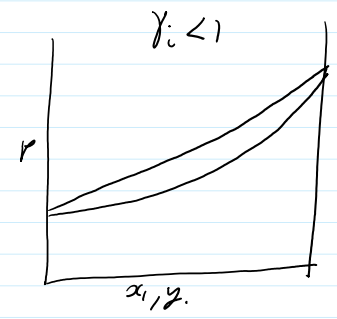
non ideal P-graph < γi 1

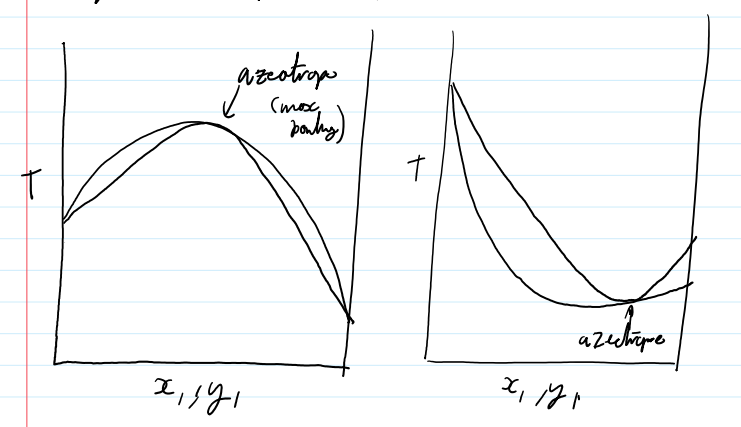
azeotrope-liquid and vapor composition are the same

T-graph 1. γi>1 2.γi<1

bubble point

the condition at which the first trace of gas(bubble) appears in the saturated liquid

dew point

condition at which the first drop of liquid appears in the saturated vapor

equilibrium condition

μ_i,L=μ_i,V f_i,L=f_i,V

activity coefficient equation

γi=ai/xi

a_i=

f_i(T,P,x)/f_i(T,P,pure i)

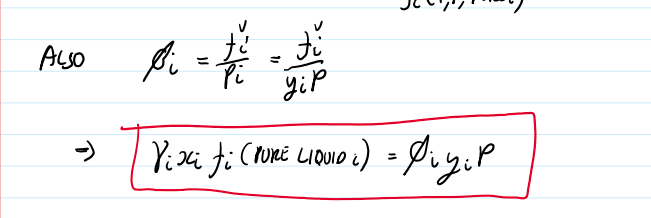
what does this equation reduce to if an ideal gas mixture and what is the pure component vapor pressure is low such that fi(PiL)=Pi^VP

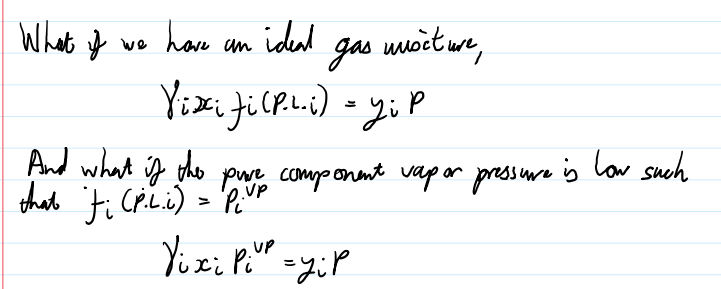
what is this equation reduced to if the liquid is ideal Raoults law

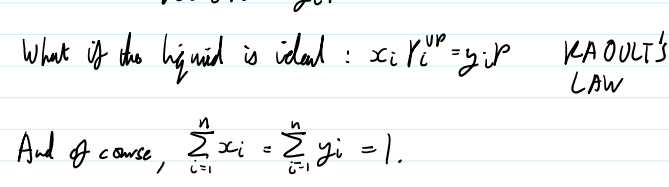
dew and bubble point ideal system(Raoults Law)

Henry’s Law

if above the critical point of a fluid, also assume that none of the species “dissolves“ in the liquid

used in dilution solutions

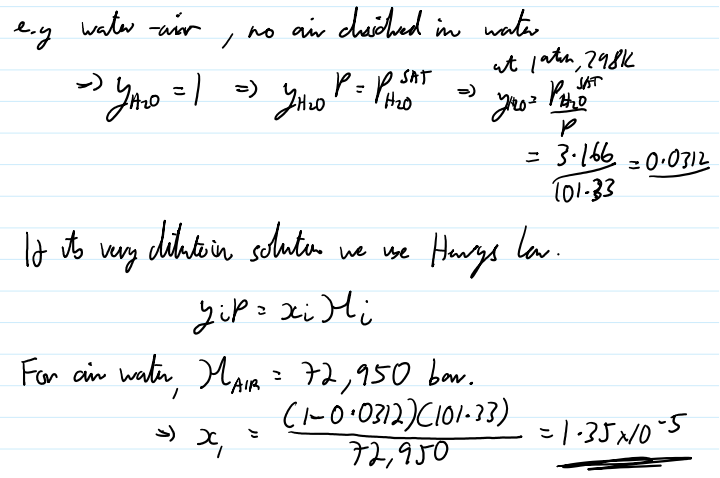
at low vapor pressure can assume an ideal gas but want to keep potential non-ideal in the liquid phase

can rearrange the formula

can use k-chart values

if y γ_i > 1,

there will be more of a component in the vapor phase from predicted by Raoult’s Law

the component doesn’t like its neighbor in the liquid phase

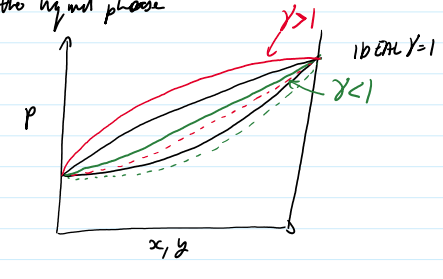
if y γ_i < 1

there will be less of the component in the gas phase then predicted by Raoults law

components like to be in the liquid phase with its new friends

How to get the excess gibbs equation from the difference in chemical potential

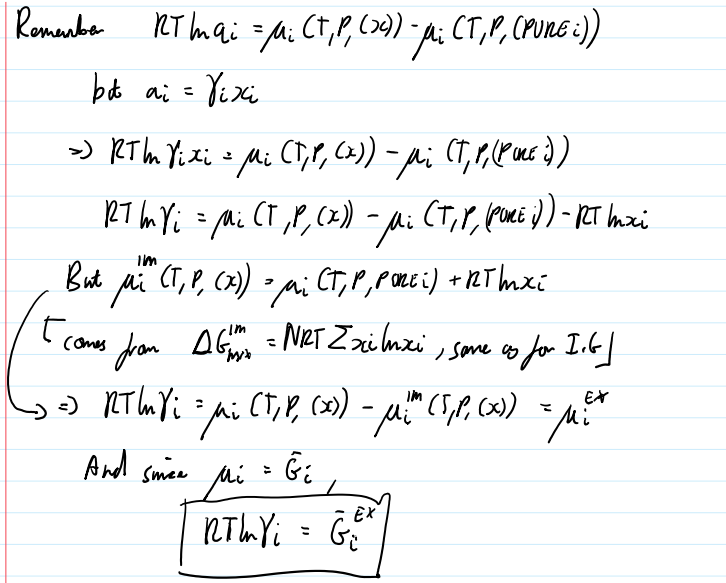
How to get excess gibbs equation from the gibbs duhem equation

in a binary system, if we have one actual coefficient, we can get the other

can use the general property of partial molar quantities

if we have VLE data, we can

fit the values of γ_i and get G^E

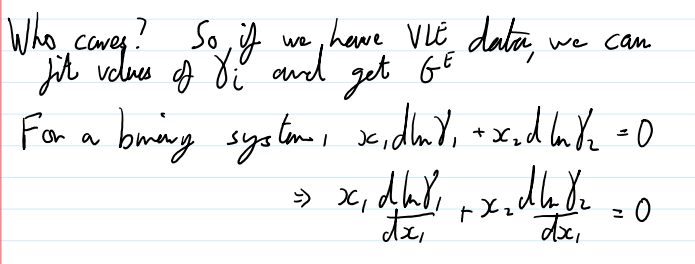
for any given fit equation for the excess G

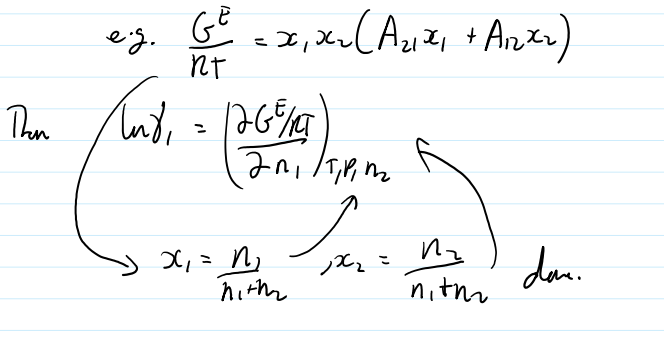
standard liquid-liquid equilibrium

common assumption in LLE is that although two phases are relatively pure eg. not much water in the oil and vice-versa from this we use γ_i,l = γ_2,ll = 1

we expect the entropy of a phase separated system to be lower than a mixture how does this fit with minimizing Gibbs

conductive of stability for a binary system

case where :One constant Margules equation- G^EX= cx₁ x2

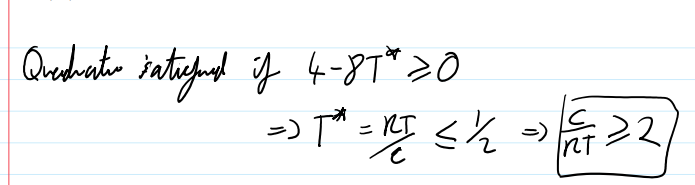
quadratic satisfaction if

so we get two phases for large c-parameter and/or low T—> entropy is overpowered by large non-ideality in the mixtures.

As T incr. C decr. entropy wins again

for VLLE, there is an additional phase but roles + m remain the same

degrees of freedom 2-3+2=1 Binary

• eg. T for 3-phases determines the system

generally need to solve the system numerically

f_i,v=f_i,L=f_i,L2

often simplify since the liquids are immiscible

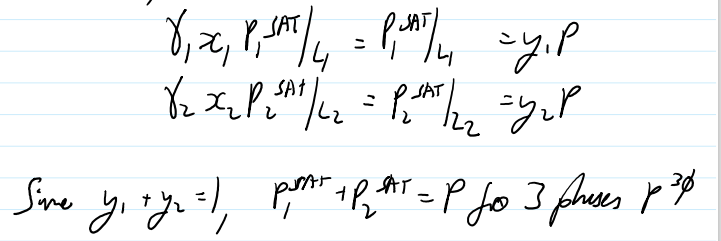
Boiling point elevation why does salt water boil at higher T

Let liquid solution 1 with salt 2 in it.

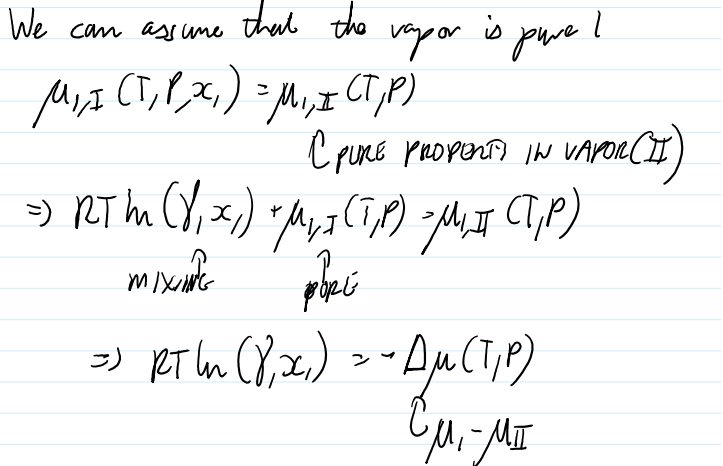
Δμ(T,P) is the chemical potential difference of the pure solvent in phase l vs. phase ll

T must be close to the boiling point of the pure species at which point

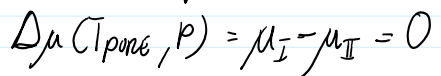
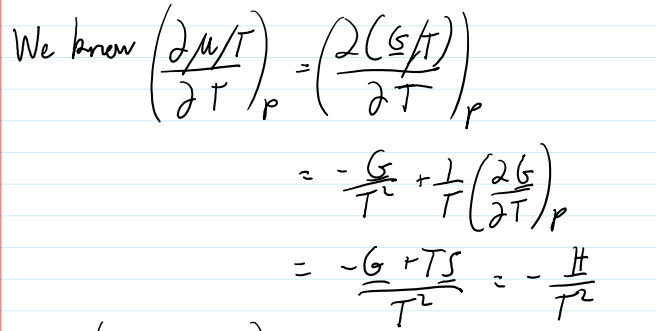
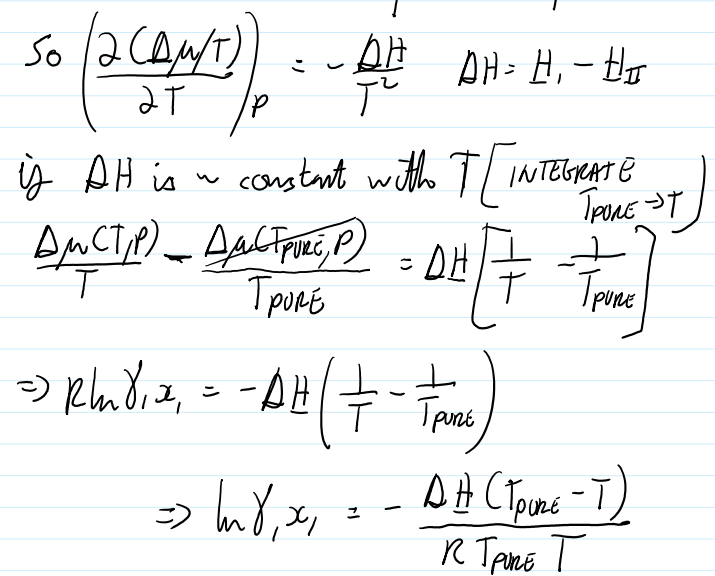
for dilute solutions

Phase l liquid, phase ll solid