Topic C.1 Simple harmonic motion
1/14
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
15 Terms
What is the definition of simple harmonic motion?
Acceleration is directly proportional to displacement
Acceleration acts in opposite direction to displacement
a = -(ω2)x
How do kinetic energy, potential energy, acceleration. and velocity change during SHM
At maximum displacement:
Potential energy and acceleration are at maximum
Velocity is zero and kinetic energy are zero,
At equilibrium:
Potential energy and acceleration are zero
Velocity and kinetic energy are at their max
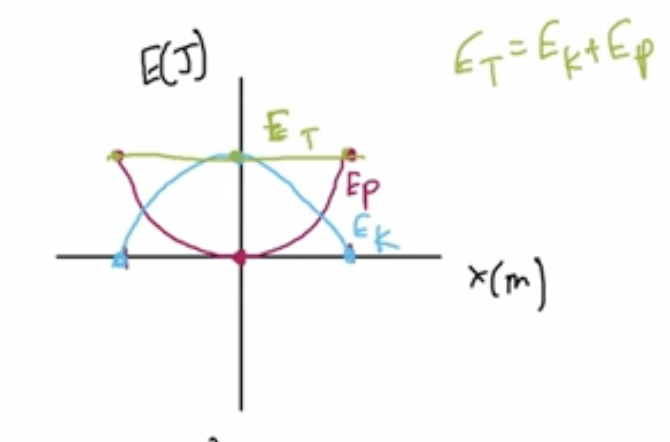
Graph for total, kinetic, potential energy against displacement
Kinetic is maximum at x=0, potential is maximum at edges (max displacement), total is straight line at top (Ek+Ep), smooth curve connecting
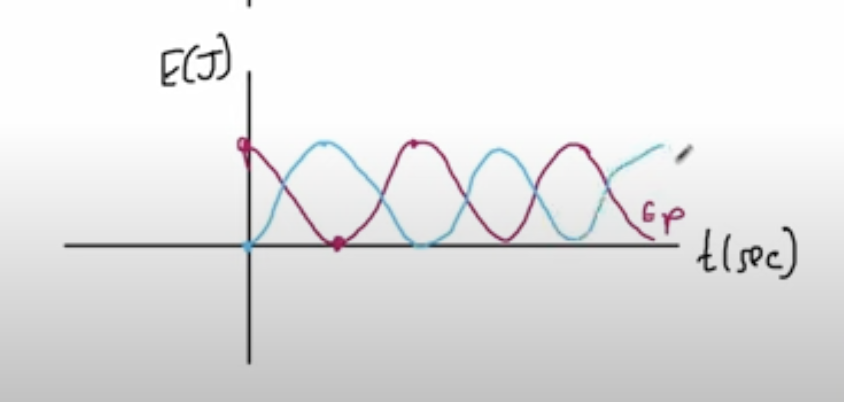
Graph for total, kinetic, potential energy against time
Potential starts at max value, kinetic starts at zero (as x=0 at t=0), total is straight line (Ek+Ep)
What is angular frequency (ω)
2pi/T, similar to how frequency is 1/T
How to get the frequency from acceleration-displacement graph?
Find gradient (square of angular frequency, ω2)
Rearrange for T
Equate to 1/F
Solve F

Displacement equation for SHM + graph
Displacement starts at 0 (because sine graph) assuming no phase angle shift
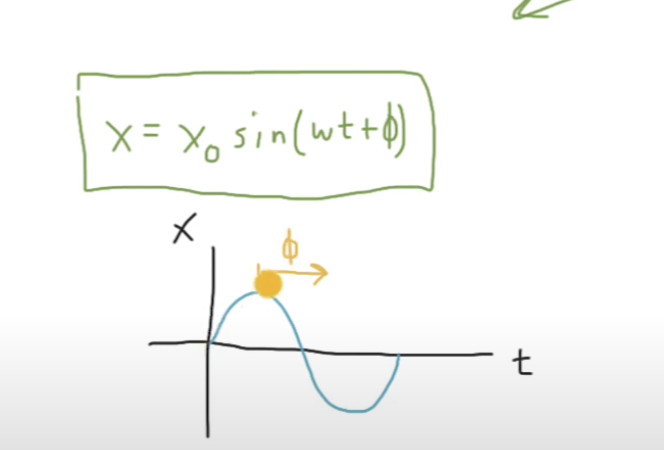
Phase angle
Graph is shifted by portion of cycle equivalent to the portion of 2pi that the phase angle is
Example of how phase angle works: if T = 8s, then pi/4 phase angle would cause it to shift by 1s, as pi/4 is 1/8th of 2pi and 1s is 1/8th of 8s
A useful phase angle to know is pi, because it causes the output of the function to be negative.
Positive phase angle is leftwards shift, negative is rightwards (opposite of what is expected)
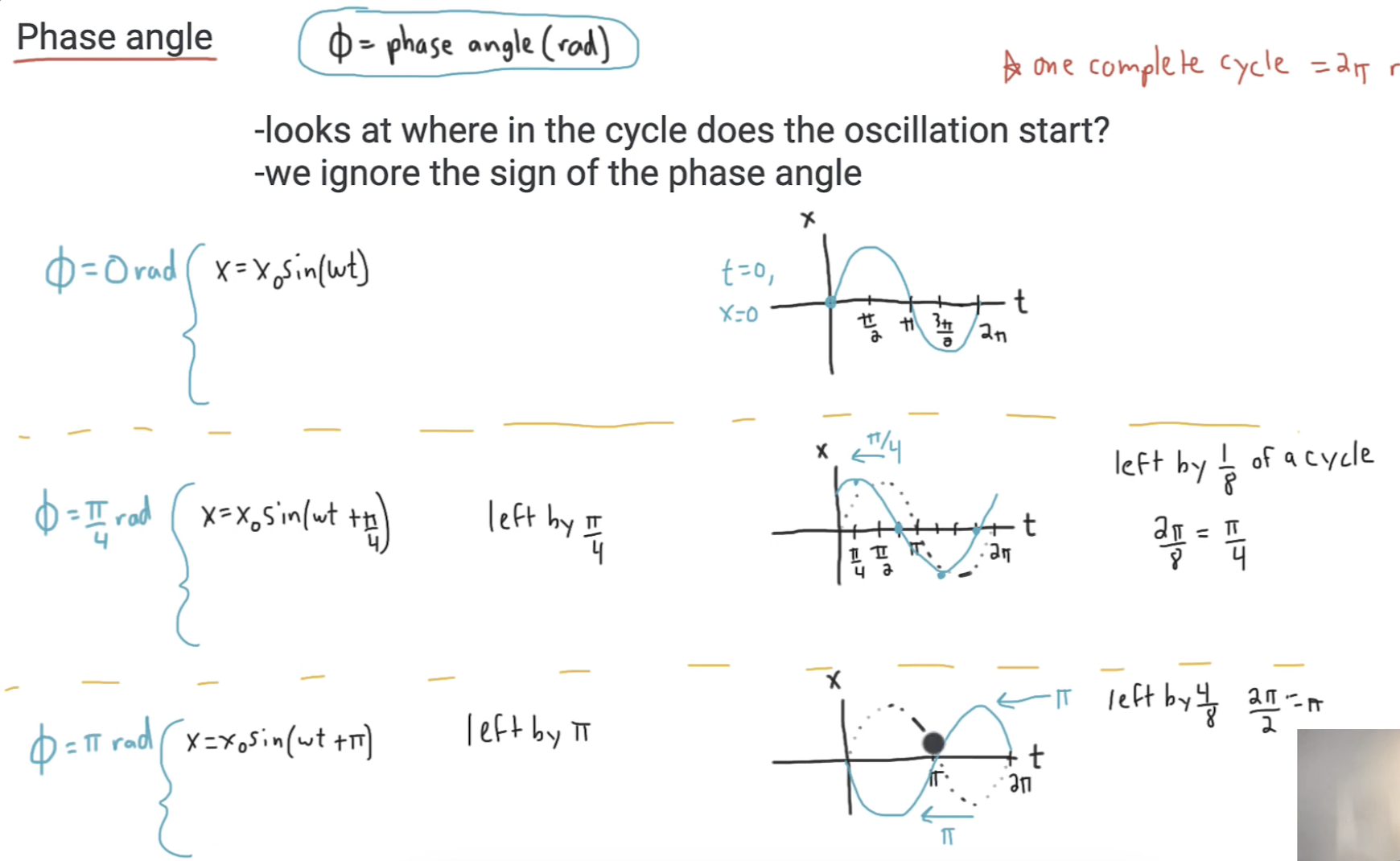
Forces acting during pendulum motion
Concept: T must be greater than mg when bob is moving in circle, as centripetal force is required
Equilibrium position: T larger than mg, centripetal force is maximum
Halfway: T still larger than mg, centripetal force is greater than 0
Max displacement: T is equal to mg, centripetal force is 0
Restoring force: mgsinθ is the restoring force, restoring force always acts perpendicular to tension
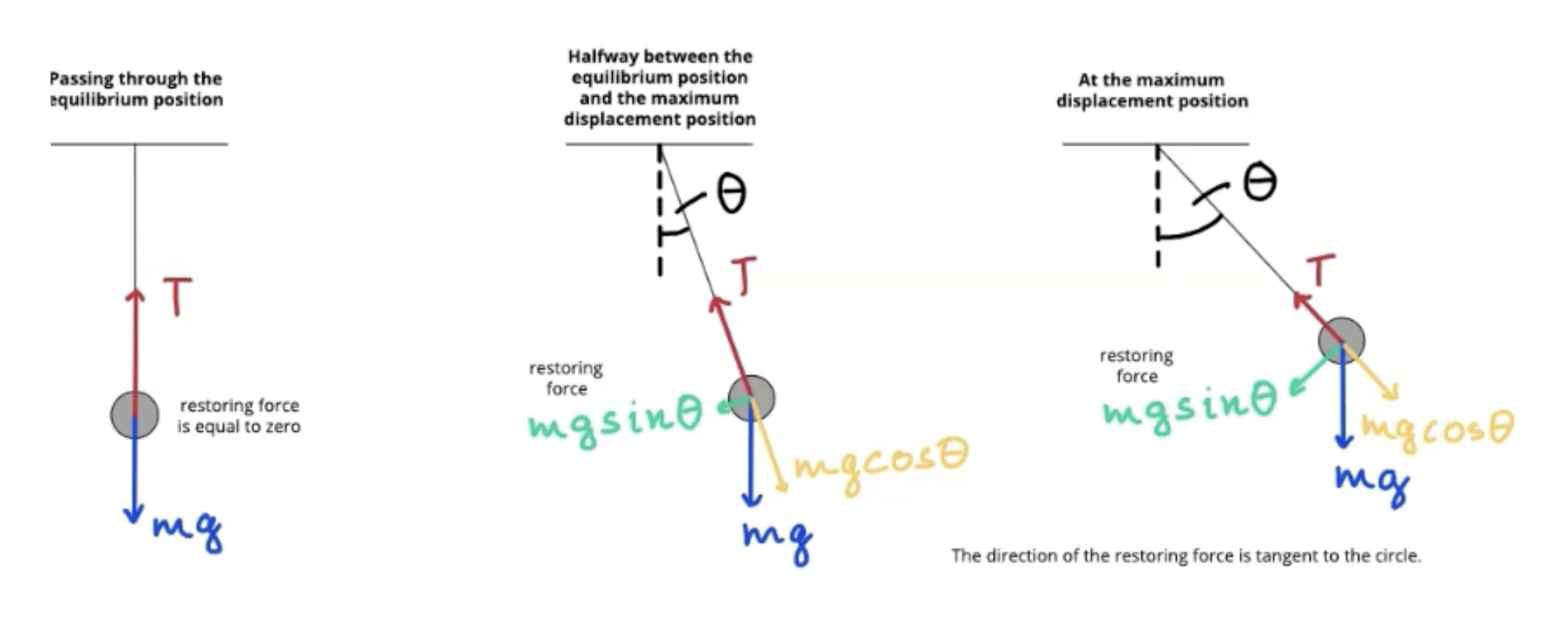
Max displacement, velocity, acceleration values
Kinetic energy formula derivation
Substitute formula for v in terms of amplitude and displacement into kinetic energy formula

Max kinetic energy/total energy derivation
Substitute 0 into kinetic energy formula, as kinetic energy is maximum at 0 displacement (equilibrium).
This is also equal to total energy.

How does particle oscillate with travelling wave?
Particle position on x-axis is fixed
If wave is moving right, then particle will follow wave as if it is moving leftwards, and viceversa.
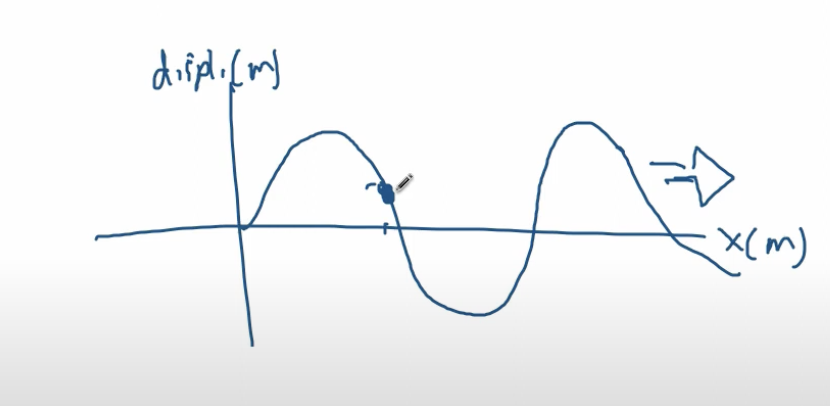
Transverse waves
Direction of oscillation is perpendicular to direction of travel
Longitudinal waves
Direction of oscillation is parallel to direction of travel