Points of Concurrency

Altitude

Name the special segment.

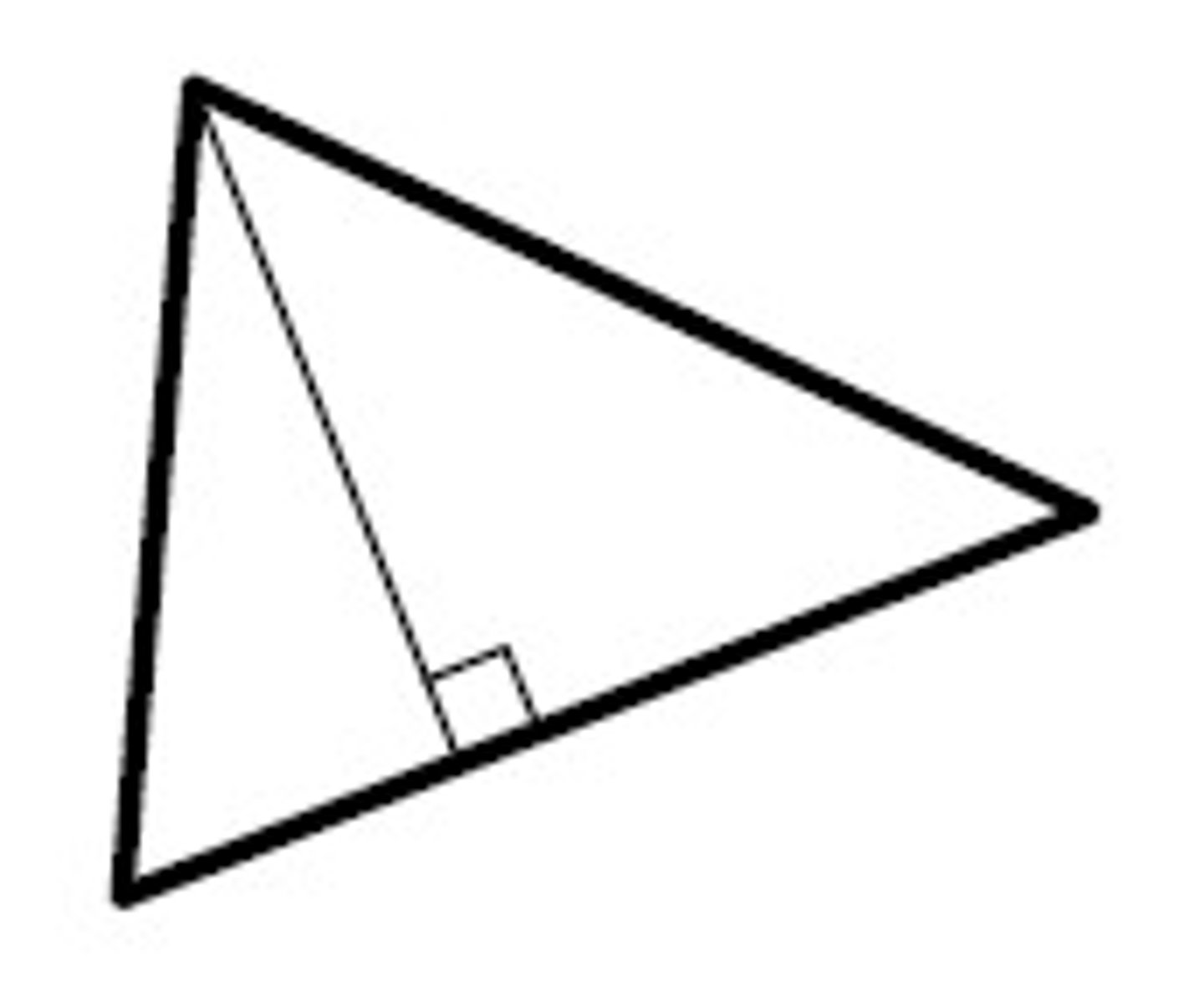
Median

Name the special segment.

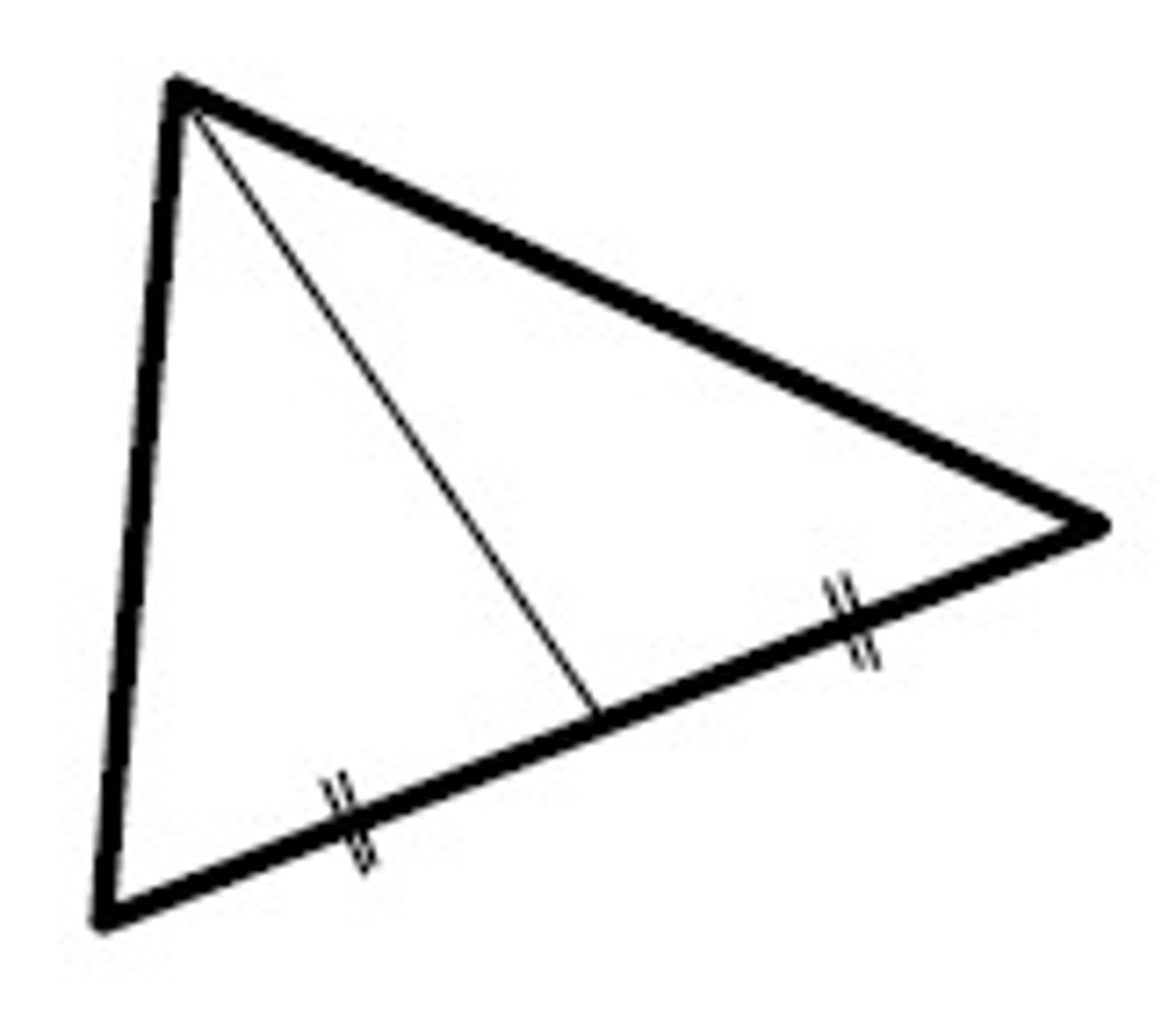
Perpendicular Bisector

Name the line shown.

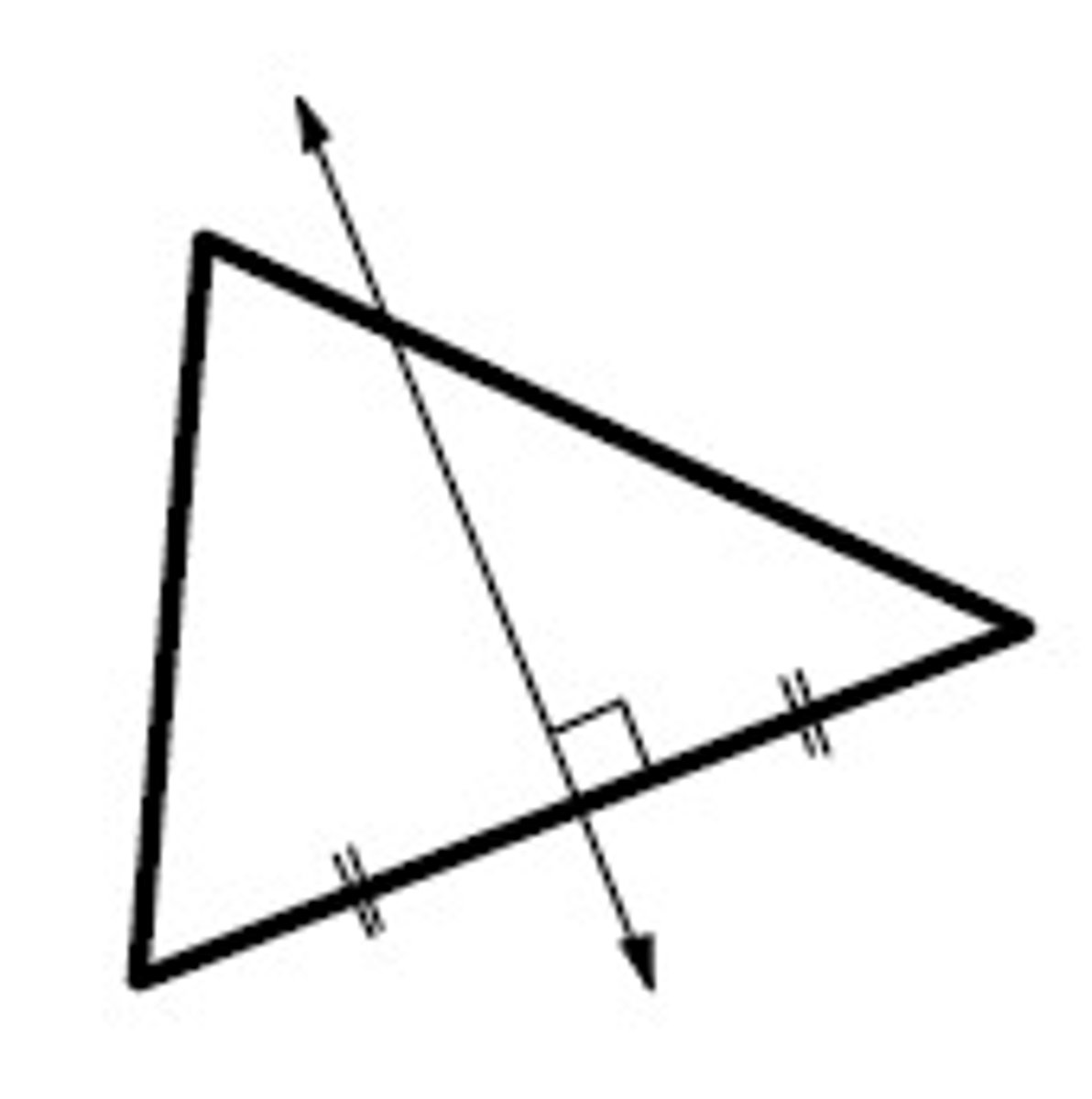
Angle Bisector

Name the ray shown.

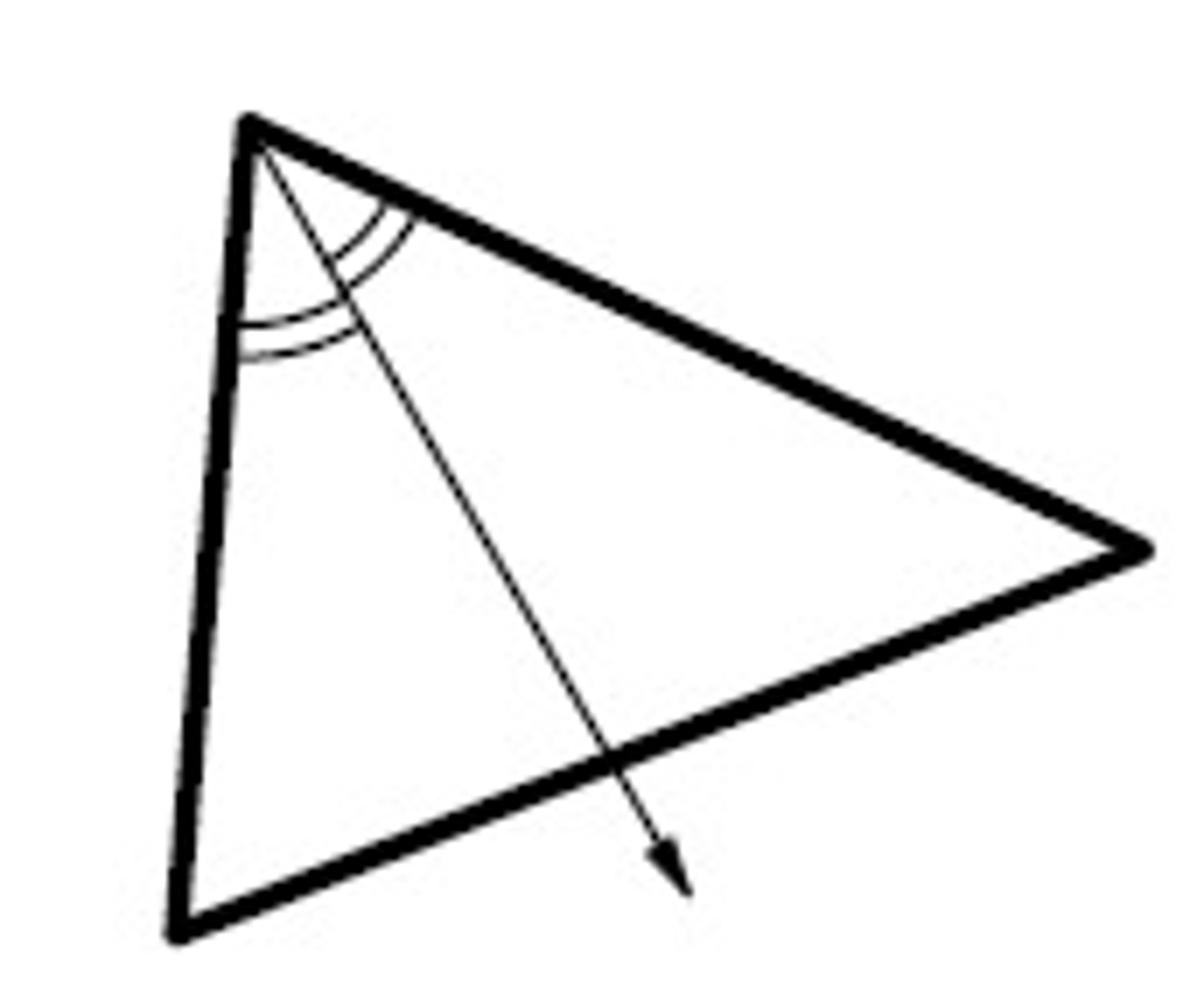
Orthocenter

The three altitudes of a triangle intersect at the ___.

Centroid

The three medians of a triangle intersect at the ___.

Circumcenter

The three perpendicular bisectors of a triangle intersect at the ___.

Incenter

The three angle bisectors of a triangle intersect at the ___.

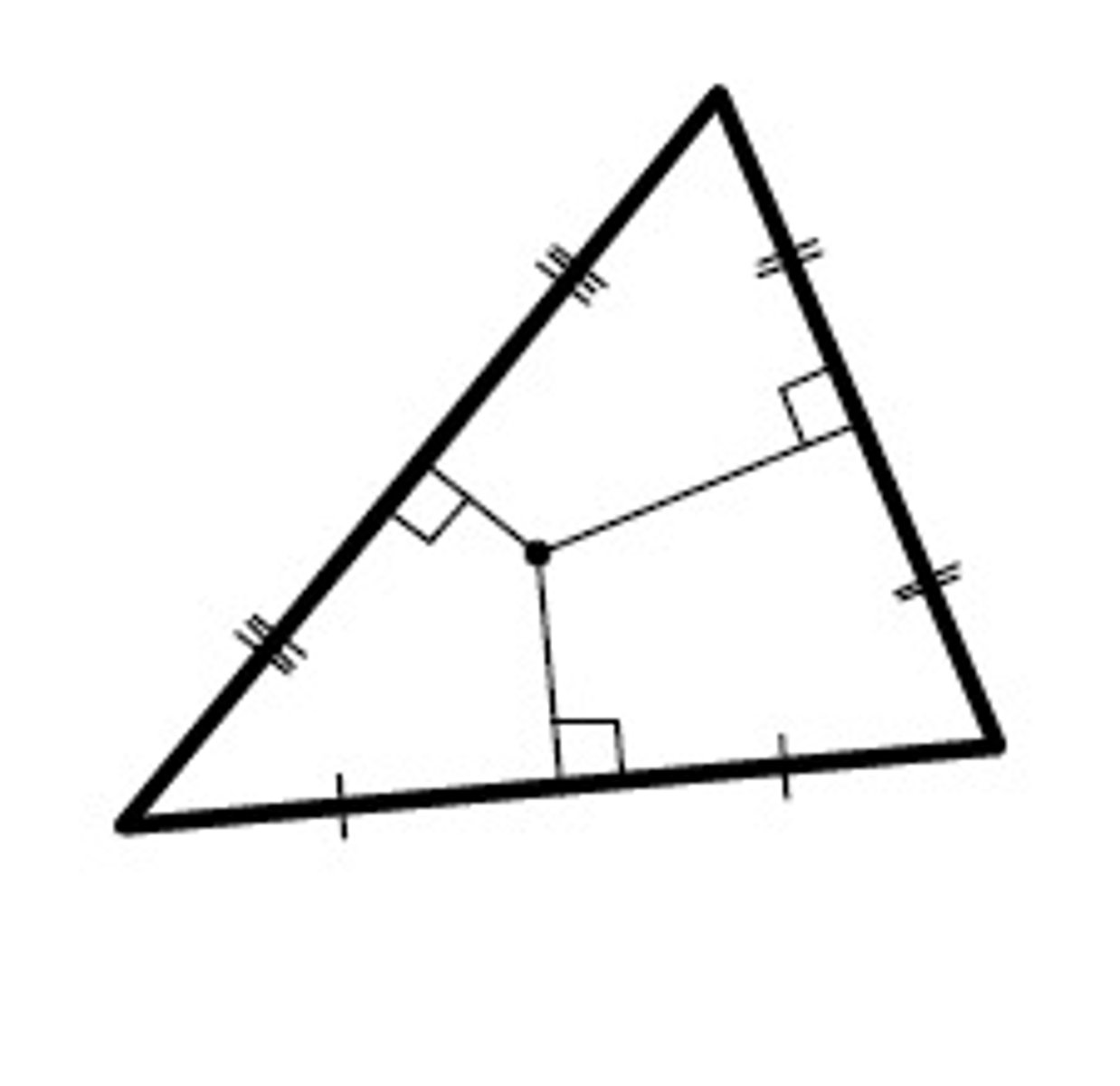
Circumcenter

It is equidistant from the three vertices of a triangle.

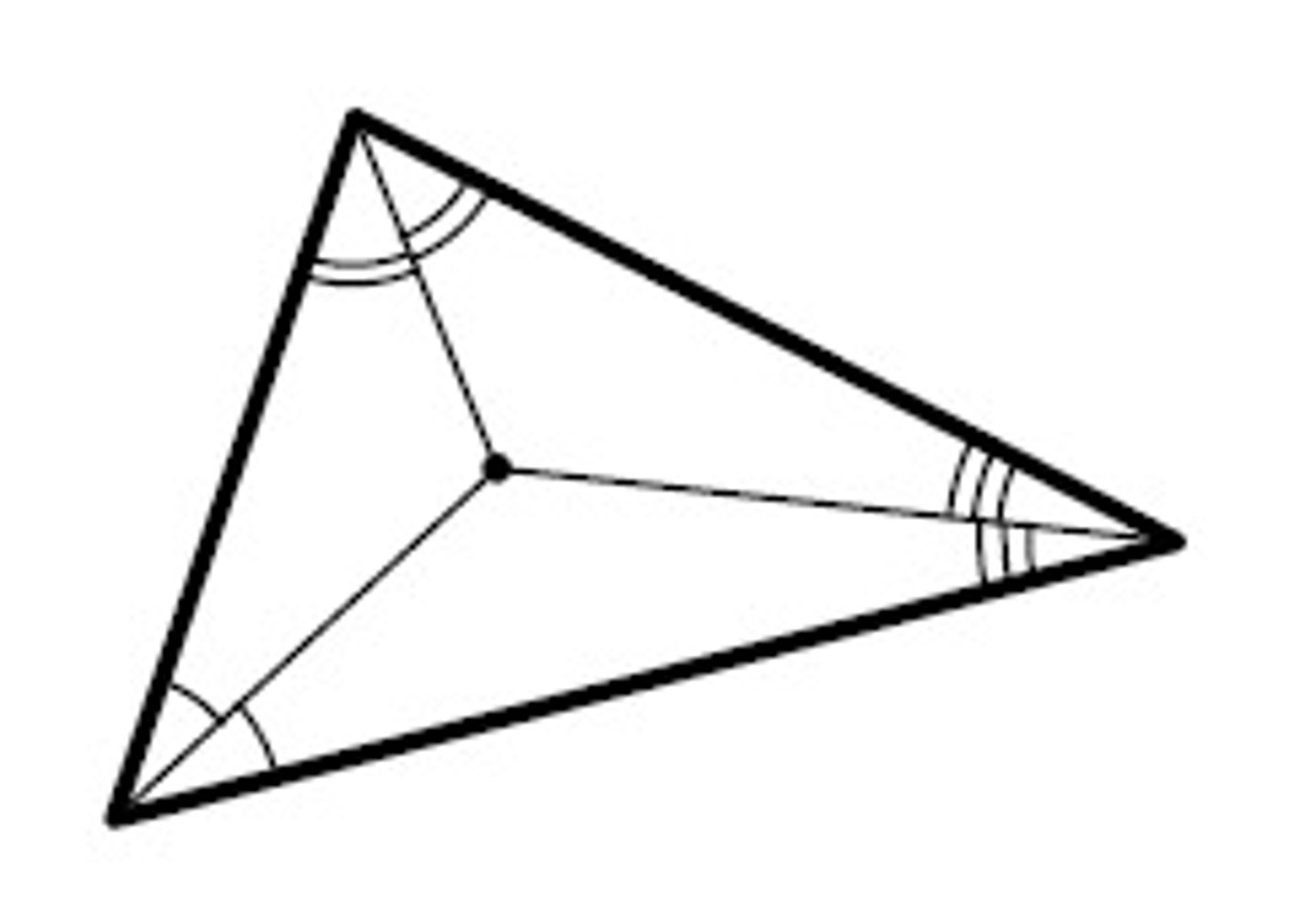
Incenter

It is equidistant from the three sides of a triangle.

Centroid

It is 1/3 the distance to the side and 2/3 the distance to the vertex.

Centroid

The ___ is the center of gravity or balancing point of a triangle.

Centroid

The triangle center shown is the ___.

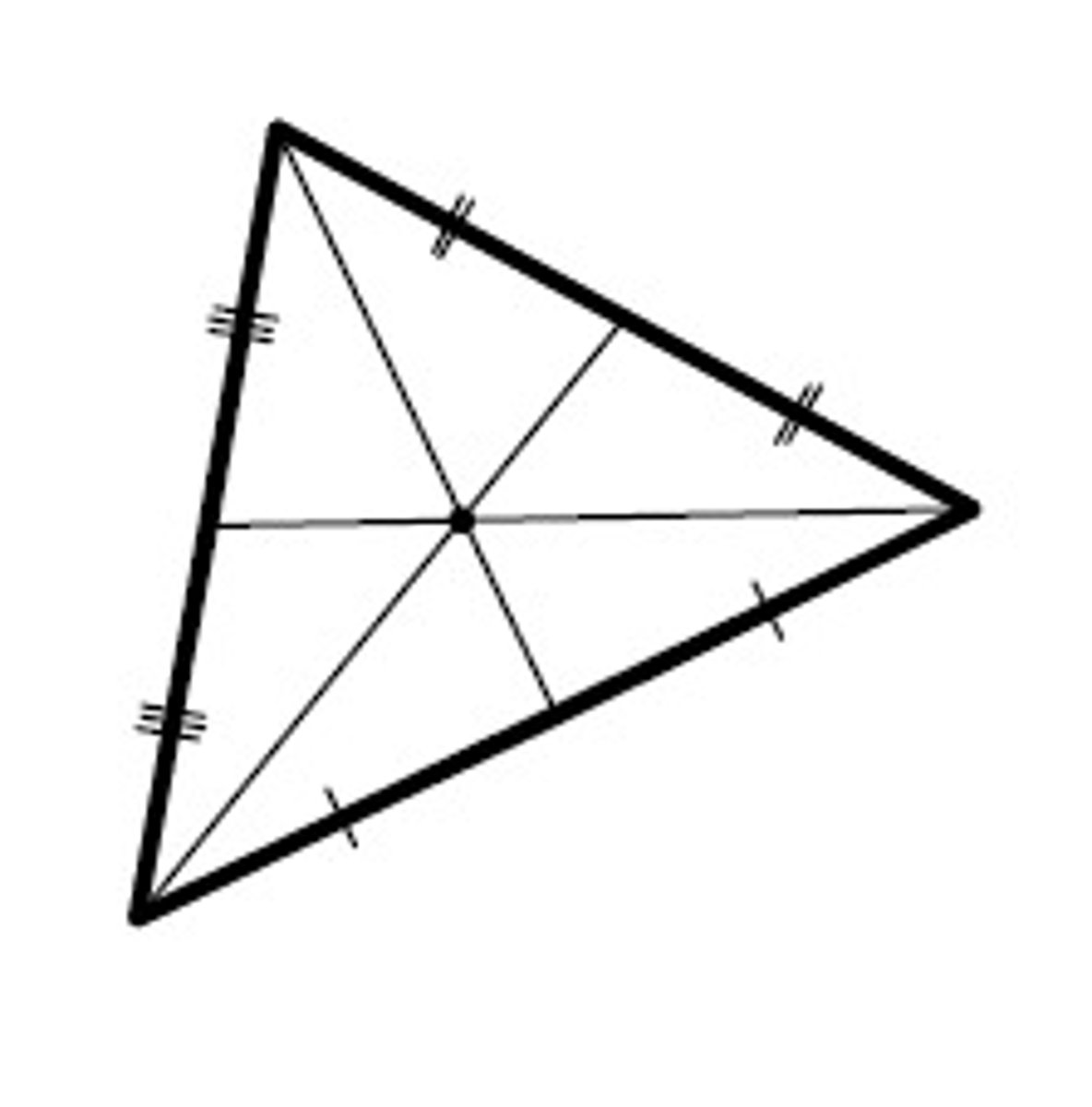
Circumcenter

The triangle center shown is the ___.

Incenter

The triangle center shown is the ___.

Circumcenter

The triangle center shown is the ___.

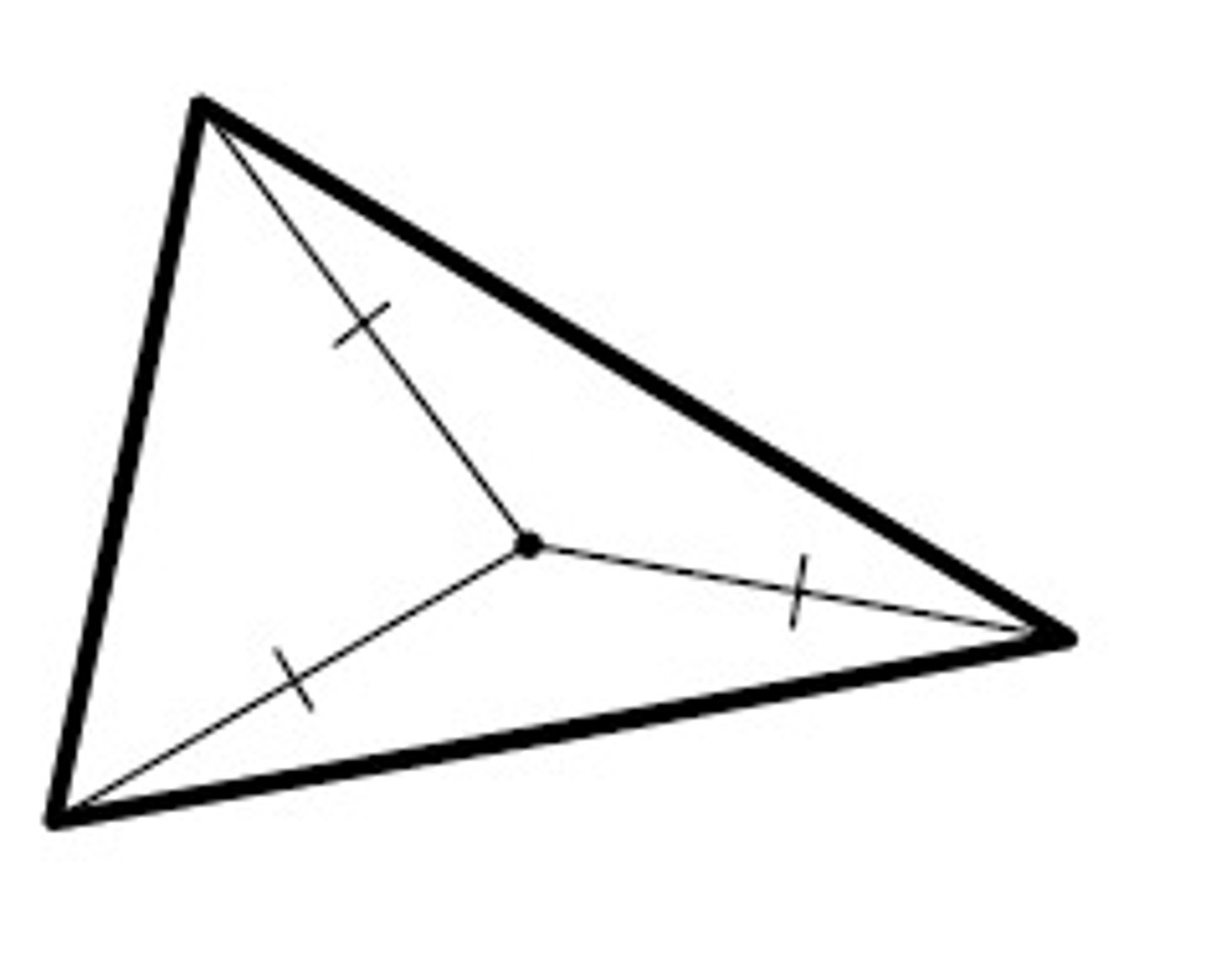
Orthocenter

The triangle center shown is the ___.

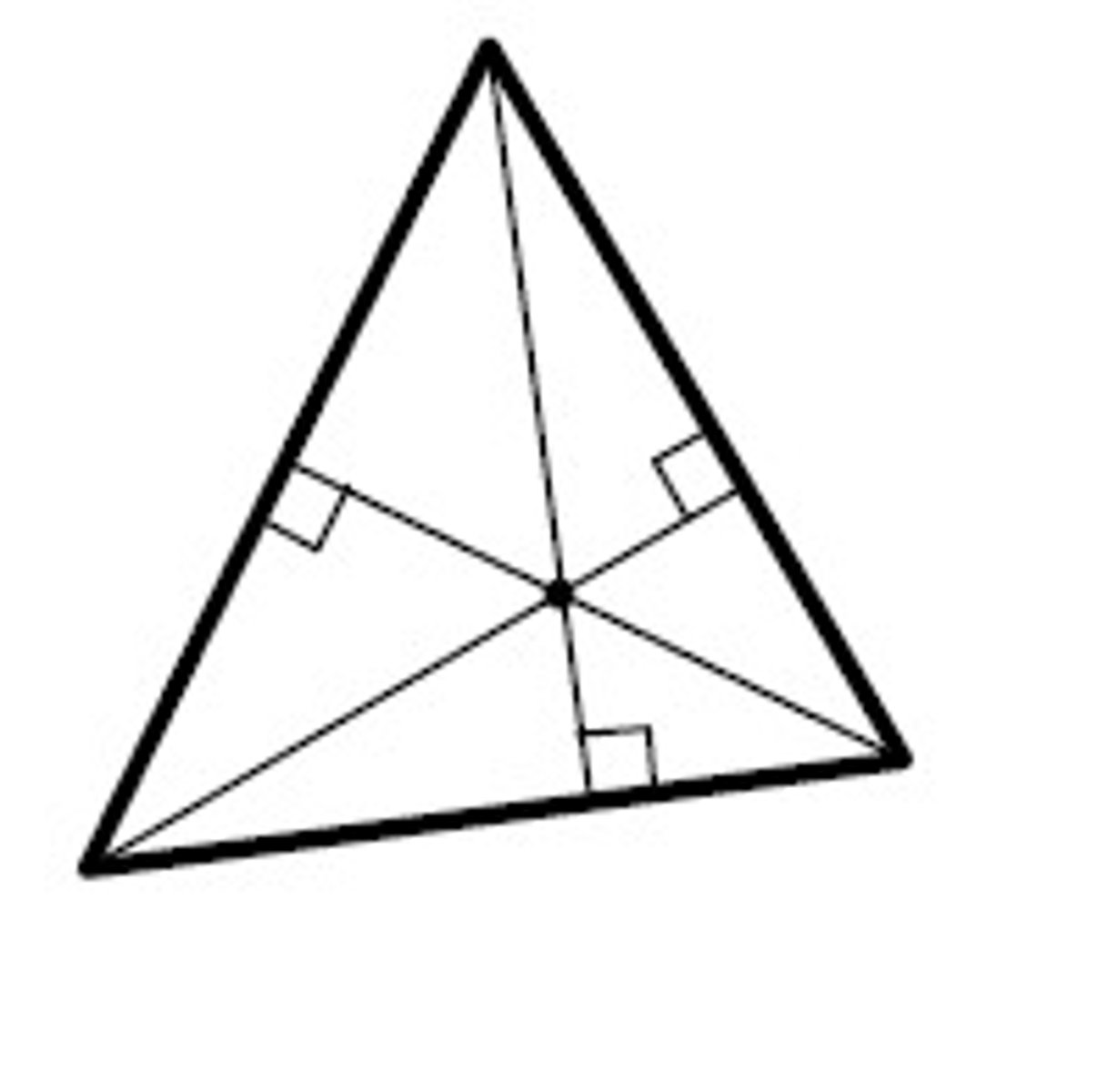
Incenter

The triangle center shown is the ___.

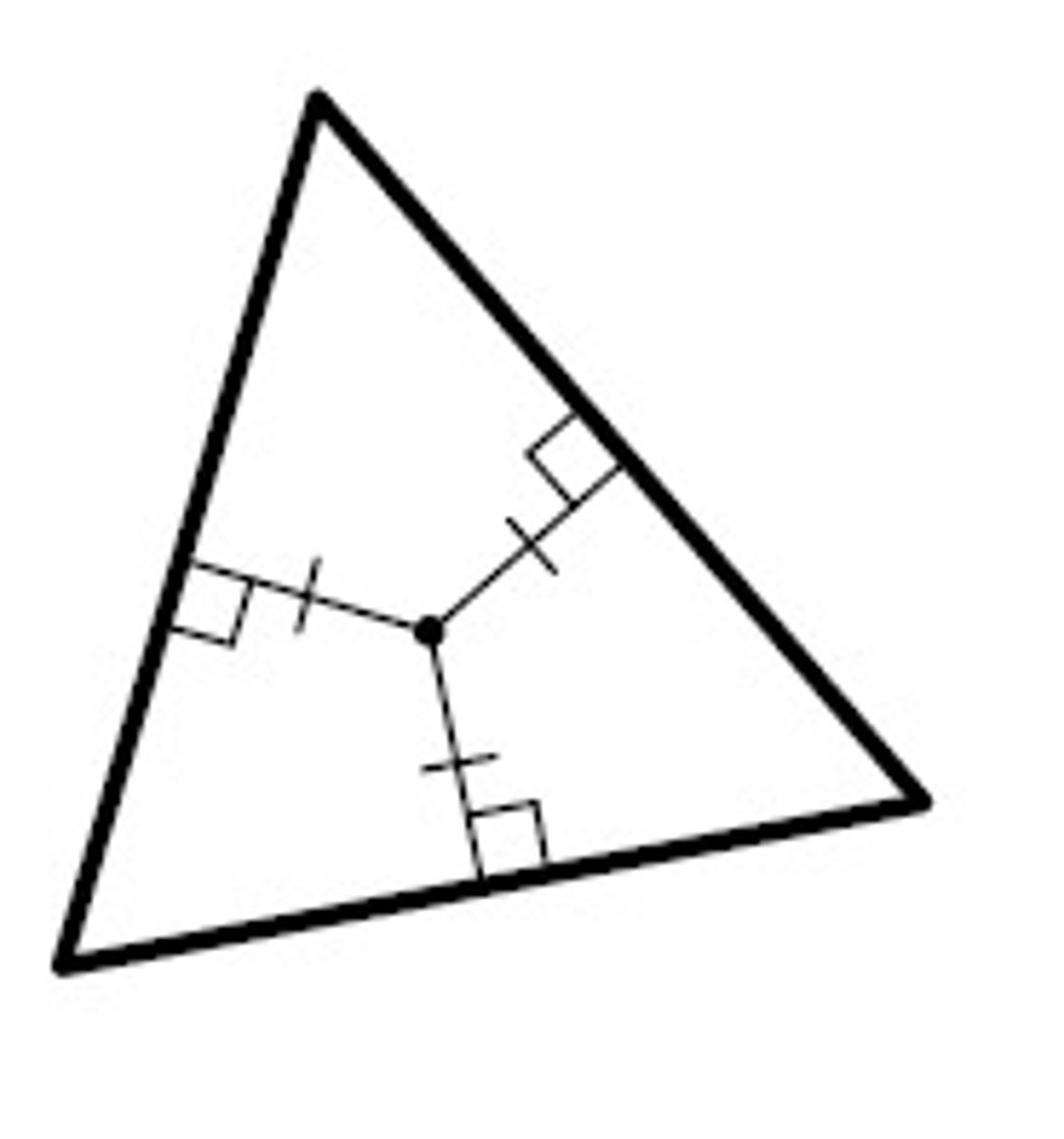
Incenter

The triangle center shown is the ___.

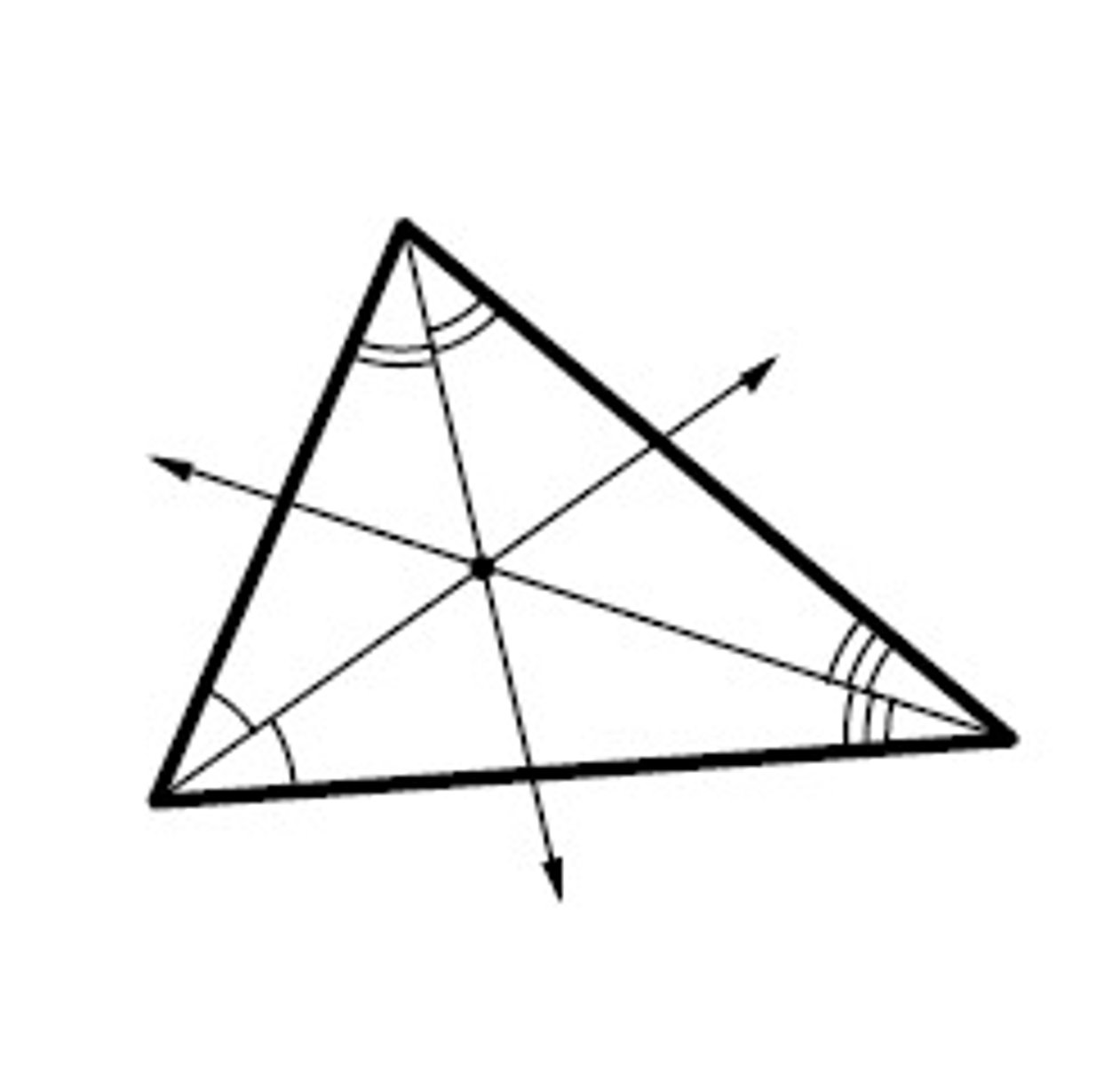
Circumcenter

The triangle center shown is the ___.

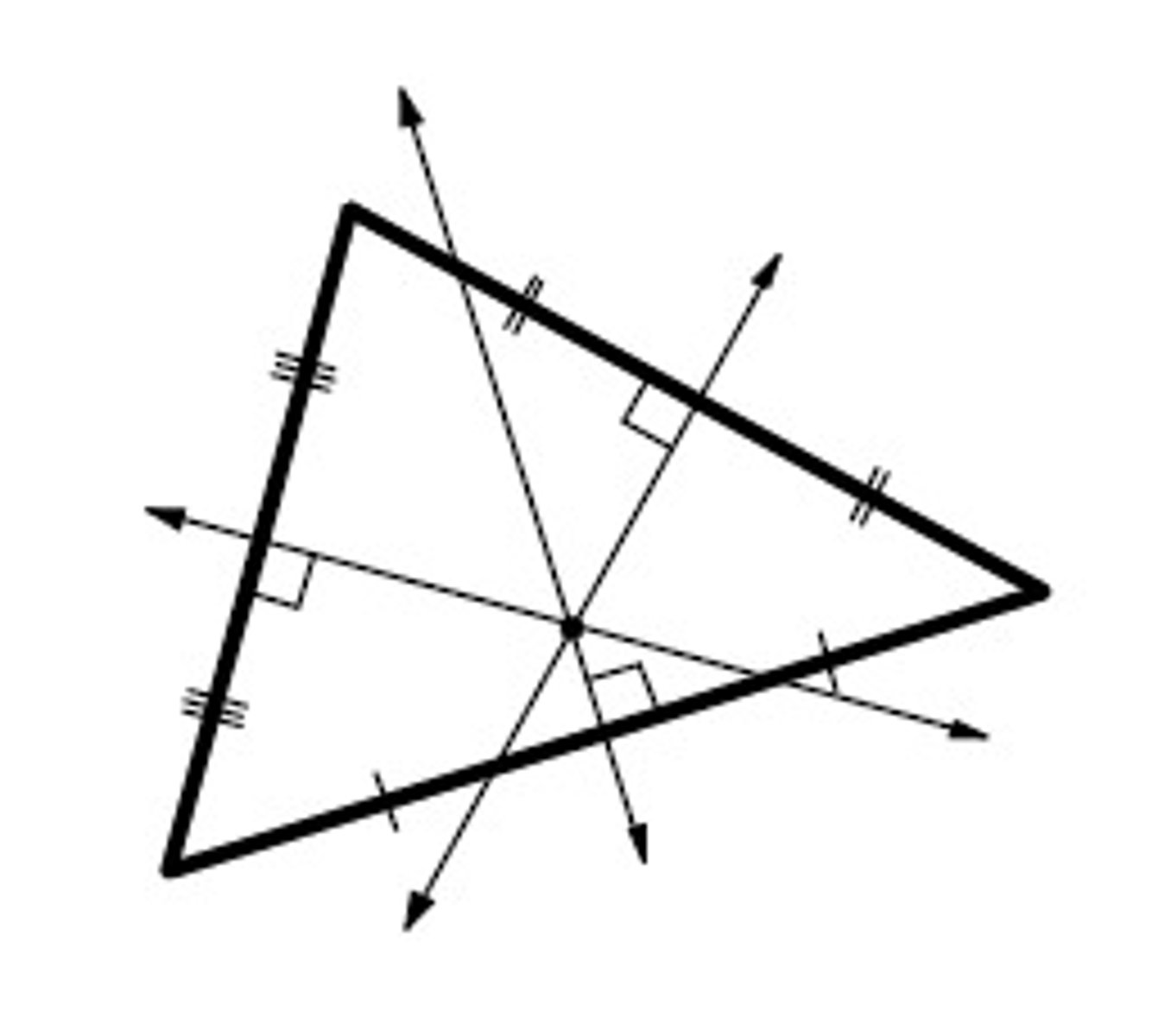
Orthocenter

The triangle center shown is the ___.

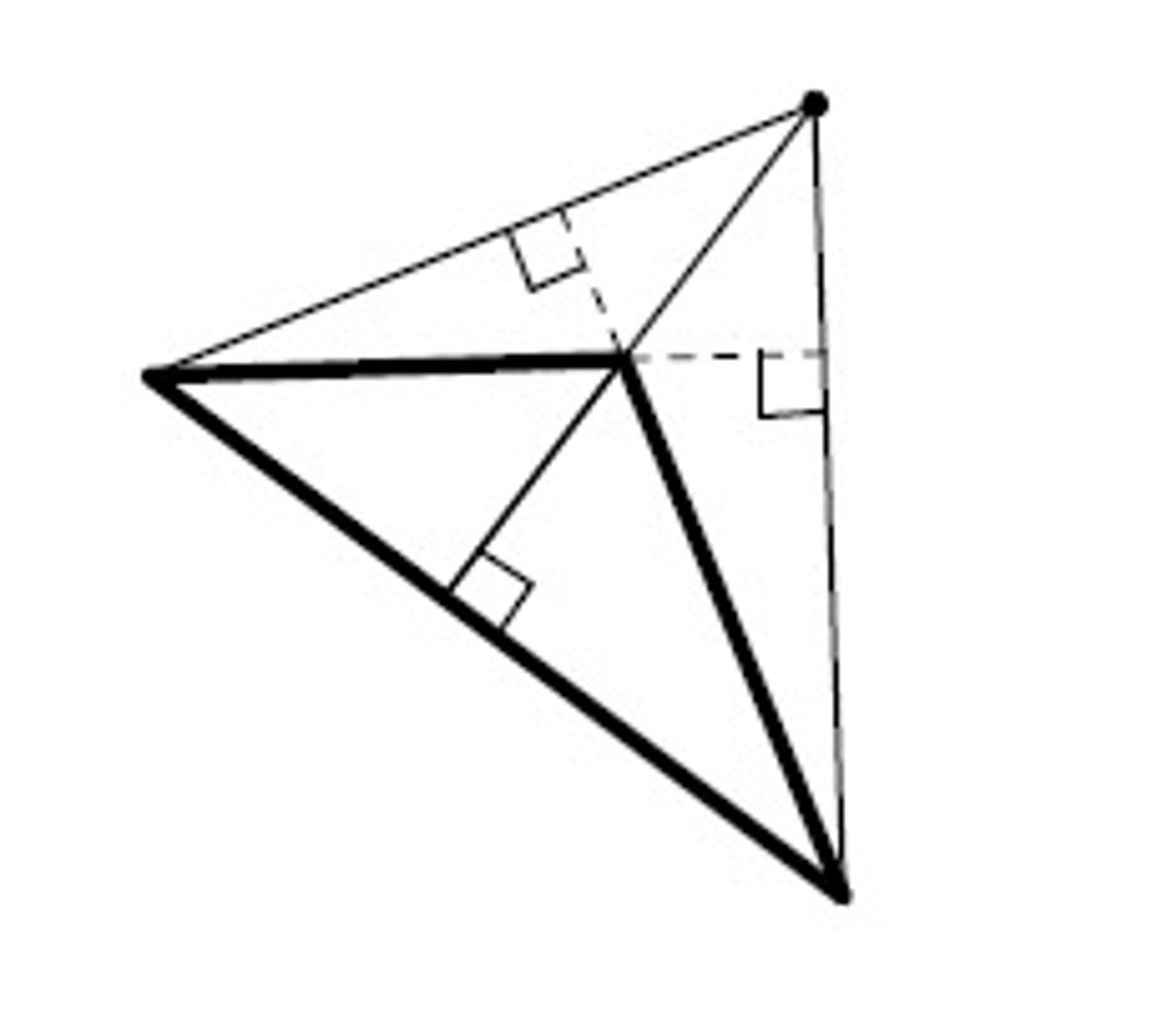
Circumcenter

The triangle center shown is the ___.

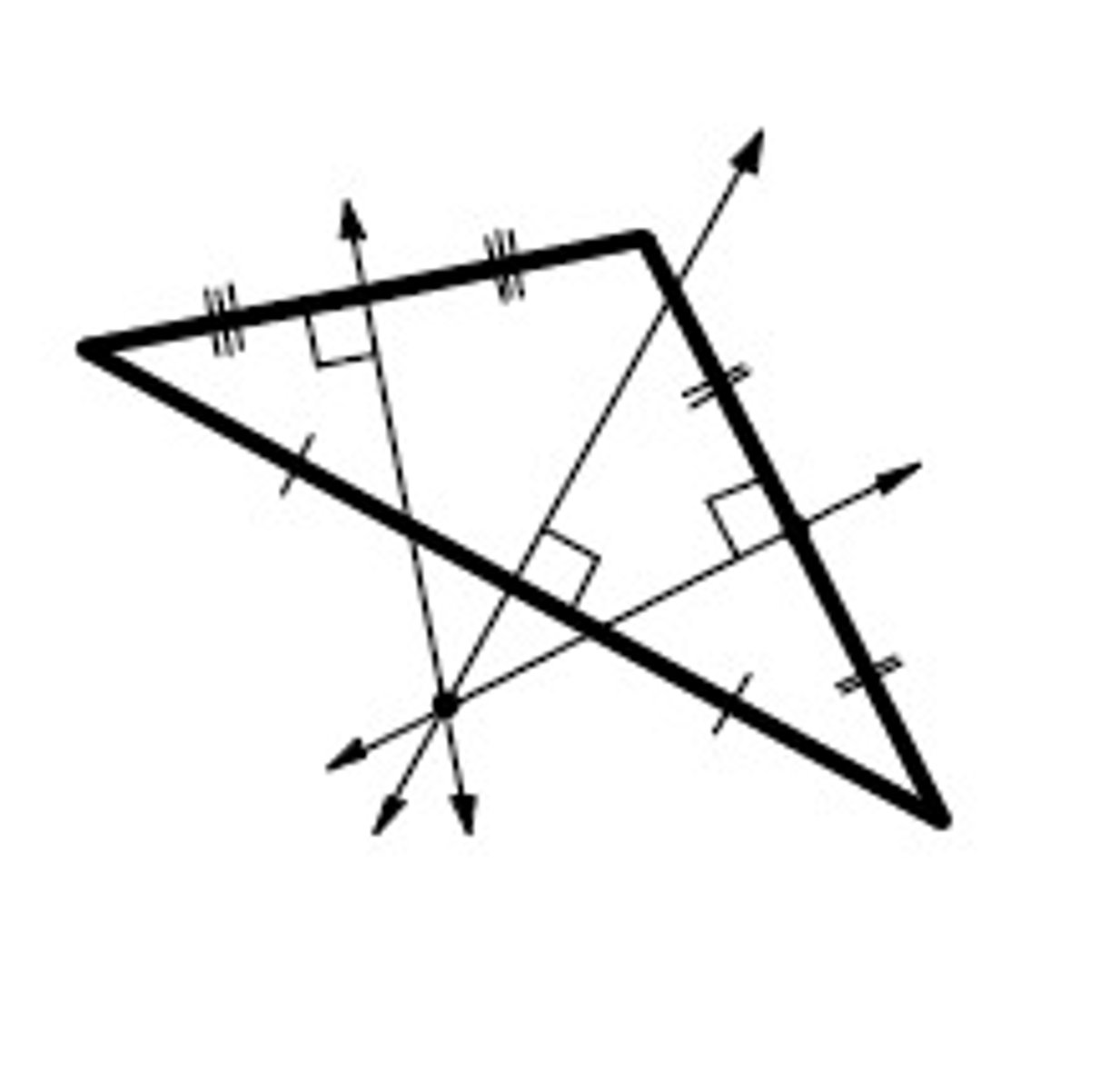
Circumcenter

The ___ of a right triangle is located at the midpoint of the hypotenuse.

Orthocenter

The ___ of a right triangle is located on the right angle.

Orthocenter and Circumcenter

Which two points of concurrency are always located outside of an obtuse triangle?

Median

The line segment joining a vertex to the midpoint of the opposite side is the ___.

Angle Bisector

The segment drawn from a vertex that bisects that angle is the ___.

Altitude

The segment that goes through the vertex and makes a right angle with the line containing the opposite side is the ___.

perpendicular bisector

The line segment that is both perpendicular to a side of a triangle and passes through its midpoint is the ___.

incenter and centroid

The ___ and ___ are always inside an obtuse triangle.

incenter

The ___ is the center of an inscribed circle.

circumcenter

The ___ is the center of a circumscribed circle.

Concurrent

When 3 or more lines intersect, they are _______.

Acute

If the orthocenter is inside, the triangle is _________.

Obtuse

If the circumcenter is outside, the triangle is __________.