Chapter 1 Theorems/info - Matrix Algebra

This covers all the important ideas and theorems in chapter 1

Theorem 1: Echelon Form

A matrix is in echelon form if:

1) All nonzero rows are above zero rows

2) Each leading entry is to the right of the one above

3) All entries below each leading entry are zero

This lets you identify pivot positions and reveals basic vs free variables.

We use it to determine consistency and counting pivots

Theorem 2 - Reduced Echelon Form

An echelon matrix is in reduced echelon form if:

4) Each leading entry is 1

5) Each leading 1 is the only nonzero entry in its column

System solutions can be read directly

Uniqueness of RREF

Every matrix is now equivalent to one and only one reduced echelon matrix.

• RREF does not depend on row operation order

• Two matrices are row equivalent - same RREF

“Is the RREF unique?” - YES

Pivot Position & Pivot Column

A pivot position is the location of a leading 1 in the RREF of a matrix

A pivot column is a column containing a pivot position

• Pivot columns - basic variables

  • Non-pivot columns - free variables

Vector Equality

Two vectors are equal if their corresponding entries are equal

• Converts vector equations to systems of equations

Linear Combination

A vector y is a linear combination of v₁,…,v_p if:

y = c₁v₁+,…,+c_pv_p

• Core idea behind span, Ax=b, column space

Algebraic Properties of Rⁿ

These justify legal vector manipulations

Matrix - Vector Product

This connects matrix equations - linear combinations

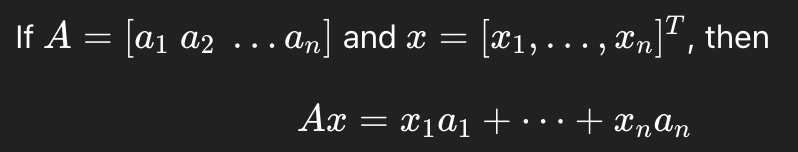
Theorem 3 - Equivalence of System Forms

The following have the same solution set:

• Ax = b

• x₁a₁+…+x_na_n = b

• The augemented matrix [A b]

We can use any method

Theorem 4 - Existence of Solutions

For an m x n matrix A, The following are equivalent:

• Ax = b has a solution for all b ∈ R^m

• Columns of A span R^m

• Every b is a linear combination of columns of A

• A has a pivot in every row

Fast consistency test and no row by row solving needed.

Homogeneous Systems

A homogeneous system Ax = 0 always has the trivial solution.

Nontrivial solutions exist = free variables exists

Parametric Vector Form

When free variables exists, solutions can be written as:

• Required final form on many problems

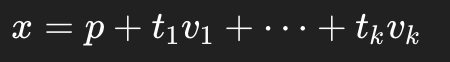
General Solution of Ax = b

If Ax = b is consistent, then:

solutions = particular solution + solutions of Ax = 0

• “Describe all solutions” - use this

Linear Independence

{v₁,…,v_p} is linearly independent if:

• x₁a₁+…+x_pa_p = 0

has only the trivial solution

Columns of a Matrix

Columns of A are linearly independent if Ax = 0 has only the trivial solution

Independence = no free variables

Sets of One or Two vectors

• One vector: independent - not zero

  • Two vectors: independent - neither is a scalar multiple of the other.

Theorem 7 - characterization of Dependence

A set of ≥ 2 vectors is linearly dependent if one vector is a linear combination of the others.

Lets you conclude dependence without row reducing