2.5 - 2.7

Set Identity

An equation involving sets that is true regardless of the contents of the sets in the expression.

Associative Laws

Commutative Laws

Distributive Laws

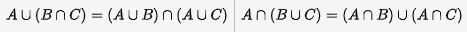
Identity Laws

Domination Laws

Double Complement Laws

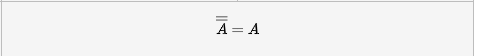
Complement Laws

De Morgan’s Laws

Absorption Laws

What is the entry of ordered pairs? (x,y)

The x comes first, then the y comes second

Cartesian Product

Denoted A X B, it is the set of all ordered pairs in which the first entry is the A and the second entry is the B.

It is important to know A X B is not the same as B X A, as the entry orders would be different.

Ordered triple

an ordered list of three items, denoted as (x,y,z)

n-tuple

an ordered list of 4 or more items. Denoted as (w,x,y,z), increases as the number of items increases.

How is a cartesian product with a set with itself denoted?

A X A, more generally as A^k

Strings

a sequences of characters

how do you find the length of a string?

find the number of characters in the string

what are the characters used in a string called?

the alphabet for the set of strings

Binary String

A string with the alphabet {0,1}

Bit

a character in a binary string

how is a set of binary strings with a length of n denoted?

{0,1}^n

Empty string

string with a length of 0, denoted with the symbol λ

λ = {0,1}^0

Concatenation

string obtained by putting two strings together

ex. s = 010, t = 11

st = 01011

strings can also be concatenated with a single symbol

ex. t0 = 110

What happens when you concatenate a string with λ?

You would still have the string you concatenated λ with, as the empty string wouldn’t add anything

Disjoint

The intersection of two sets are empty (A ∩ B = ∅)

Pairwise Disjoint

Every pair of distinct sets in the sequence is disjoint

Partition

A collection of non-empty subsets of A (A is non-empty) such that each element of A is in exactly one of the subsets.

ex. A = {1,2,3,4,5,6}

A1 = {1,4,5}, A2 = {2,3}, A3 = {6}

A1 - A3 form a partition of A