Chapter 2 Theorems/Info - Matrix Algebra

This covers all of the important theorems and ideas from chapter 2

Theorem 1 - Matrix addition & Scalar Multiplication Laws

Let A, B, C be matrices of the same size and let r, s be scalars:

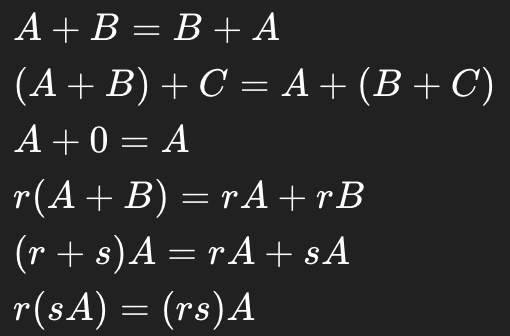
Invertible Matrix

An n x n matrix A is invertible if there exists C such that: CA = I and AC = I

This guarantees:

• The inverse is unique

• Denoted A^-1

Theorem 4 - The Invertibility Test

For A = [a b ; c d],

A invertible ad - bc doesn’t equal = 0

Guarantees:

• det A doesn’t = 0

• Explicit inverse formula exists

Theorem 5 - Unique Solution to Ax = b

If A is invertible, then for every b ∈ Rⁿ

• Ax = b has the unique soltuion x = A^-1b

“Solve Ax = b without row reducing” - use A^-1b

Theorem 6 - Algebra of Inverses

• Products of invertible matrices are invertible

  • Order reverses in inverses

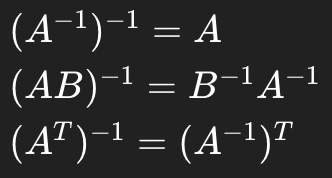
Theorem 7 - Row Equivalence & Inverses

A is invertible if A = I_n

Row reducing [A I] gives [I A^-1]

• Fast invertibility check

  • Algorithm for computing A^-1

Subspace Test

A set H ⊂ Rⁿ is a subspace if:

• 0 ∈ H

• Closed under addition (stay in the set)

• Closed under scalar multiplication

“Is this a subspace? check all three

Column Space

Col A = Span {a₁,…,a_n}

• Col A ⊂ R^m

• Always a subspace

Theorem 12 - Null Space

Nul A = {x : Ax = 0}

is a subspace of Rⁿ

• Solutions of homogeneous systems form a subspace

Basis

A basis is a leneraly independent set that spans the subspace

Guarantee:

• The coordinates are unique

Theorem 13 - Pivot Columns Form a Basis

The pivot columns of A form a basis for Col A

• Ignore non-pivot columns completely

Dimension

dim H = number of vectors in any basis of H

Guarantee:

• All bases have the same size

Rank

rank A = dim(Col A) = # pivot columns

Theorem 14 - Rank-Nullity Theorem

If A has n columns,

rank A + dim(Nul A) = n

• Instantly connects pivots and free variables

Theorem 15 - Basis Test

If H is p-dimensional:

• Any linear independent set of p vectors in H is a basis

  • Any spanning set of p vectors in H is a basis

Invertible Matrix Theorem

For A ∈ R^nxn, the following are equivalent:

• A invertible

• A = I_n

• n pivots

• Ax = 0 has only trivial solution

  • Columns of A are linearly independent

Applications of IMT

Equivalent to invertibility:

• Columns of Rⁿ

• Ax = b has a solution for all b

• x → Ax is one to one and onto

• A^T is invertible

• CA = I or AD= I for some matrix

Prove one → you get all