Algebra Formulas

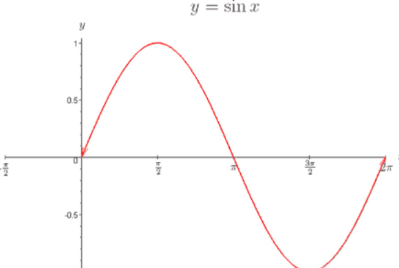
sin(x)

odd function: symmetry about the origin

def of odd: -sin(x) = sin(-x)

y/r

• r = asin(b0-x) + y

• a: amplitude

• b: period (2π/b)

• y: shift up or down

• x: shift left or right

Frequency: how many cycles occur in 2π

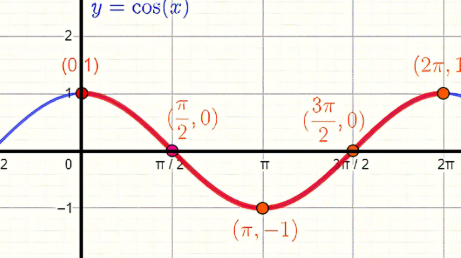
cos (x)

even function: symmetry over y-axis

def of even: cos(x) = cos(-x)

x/r

• r = acos(b0-x) + y

• a: amplitude

• b: period (2π/b)

• y: shift up or down

• x: shift left or right

Frequency: how many cycles occur in 2π

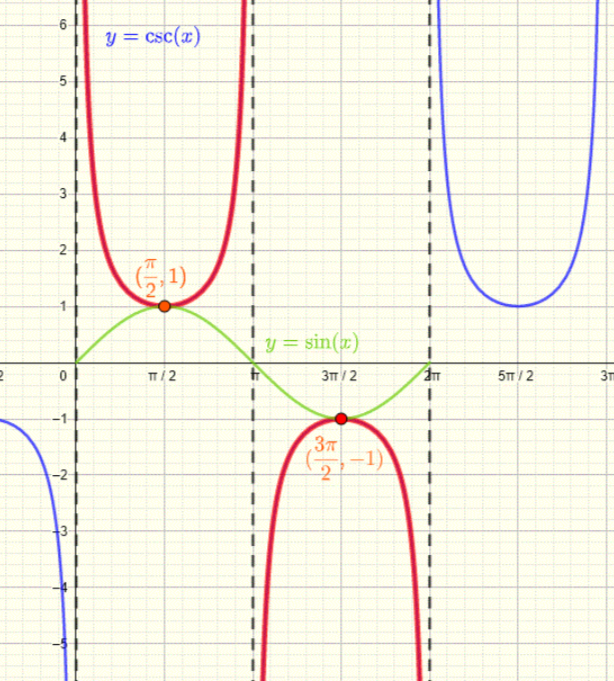
csc(x)

1/ sin(x): odd function symmetry abt the origin

1/y

def of odd: -csc(x) = csc(-x)

• sketch sin → make csc

• as sin → 0 csc → undef bc the reciprocal of 0/1 is 1/0

• sin can be infinitely small vs csc can be infinitely large bc denom vs numerator inc

Frequency: how many cycles occur in 2π

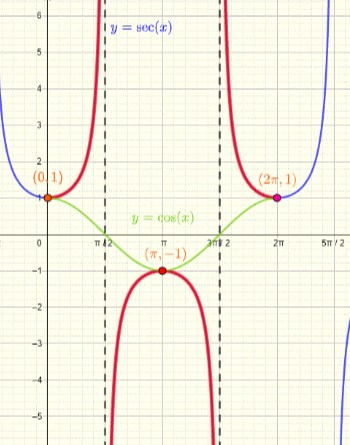
sec(x)

1/ cos(x): even function symmetry over y-axis

1/x

def of odd: sec(x) = sec(-x)

• sketch cos→ make sec

• as cos→ 0 sec→ undef bc the reciprocal of 0/1 is 1/0

• cos can be infinitely small vs sec can be infinitely large bc denom vs numerator inc

Frequency: how many cycles occur in 2π

arcsin(x) = sin^-1(x)

sin(x)

→ D: [-∞, ∞]

→ R: [-1, 1]

arcsin(x) is reciprocal + range restricted to make function

→ D: [-1,1]

→ R: [-π/2, π/2]

arccos(x) = cos^-1(x)

cos(x)

→ D: [-∞, ∞]

→ R: [-1, 1]

arccos(x) is reciprocal + range restricted to make function

→ D: [-1,1]

→ R: [o, π]

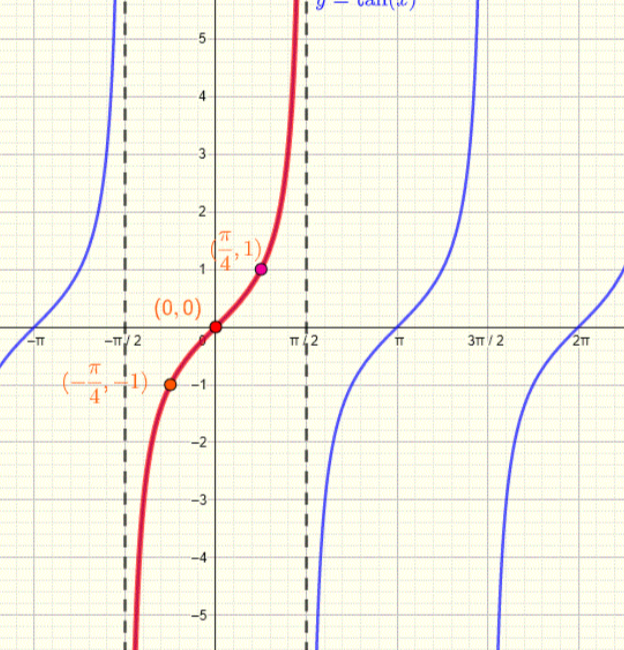
tan(x)

odd function: symmetry about the origin

def of odd: -tan(x) = tan(-x)

sin(x)/cos(x)

as tan→π/2 undef bc sin/cos = 1/0

y/x

• r = atan(b0-x) + y

• a: amplitude

• b: period (2π/b)

• y: shift up or down

• x: shift left or right

Frequency: how many cycles occur in 2π

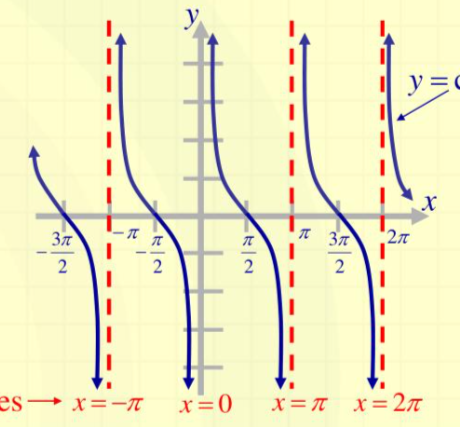
cot(x)

odd function: symmetry about the origin

def of odd: -cot(x) = cot(-x)

cos(x)/sin(x)

as cot→0 undef bc cos/sin= 1/0

x/y

• r = acot(b0-x) + y

• a: amplitude

• b: period (2π/b)

• y: shift up or down

• x: shift left or right

Frequency: how many cycles occur in 2π

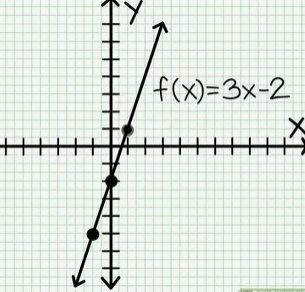
linear function

y=mx+b

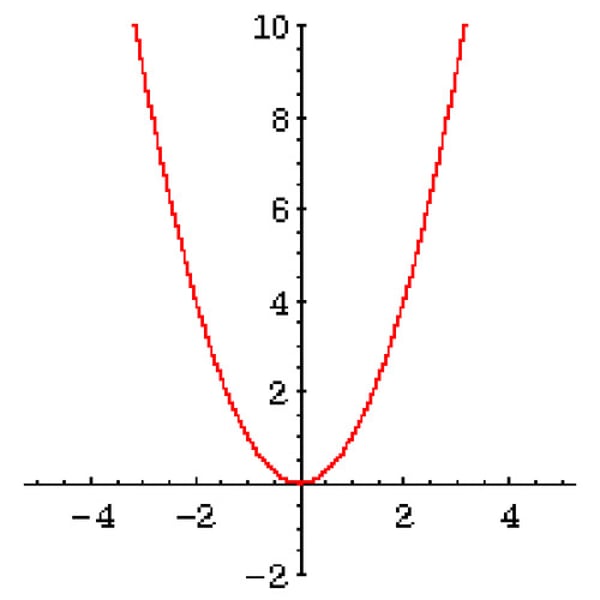
Quadratic Standard Form

y=ax^2+bx+c

Quadratic Factored Form

y=a(x-p)(x-q)

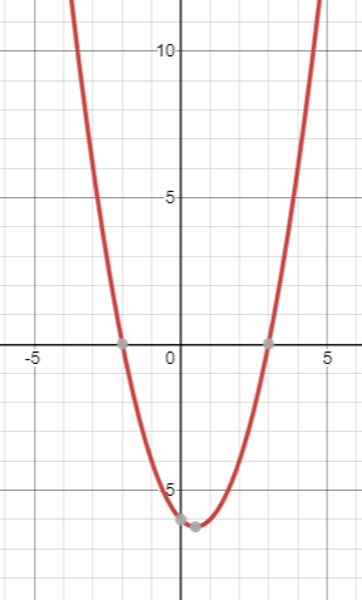
Quadratic Vertex Form

y= a(x-h)^2+k; (h,k) (even func symmetry over y-axis)

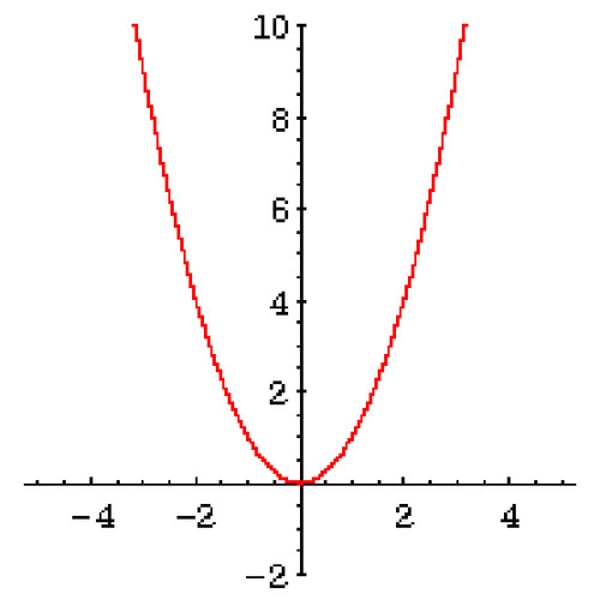
cubic function

y=a(x)^3

y=a(x+x)³ + y

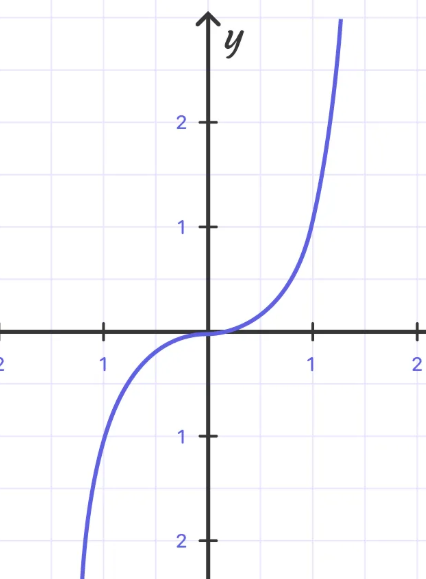
Square Root Function

y=a√x-h +k

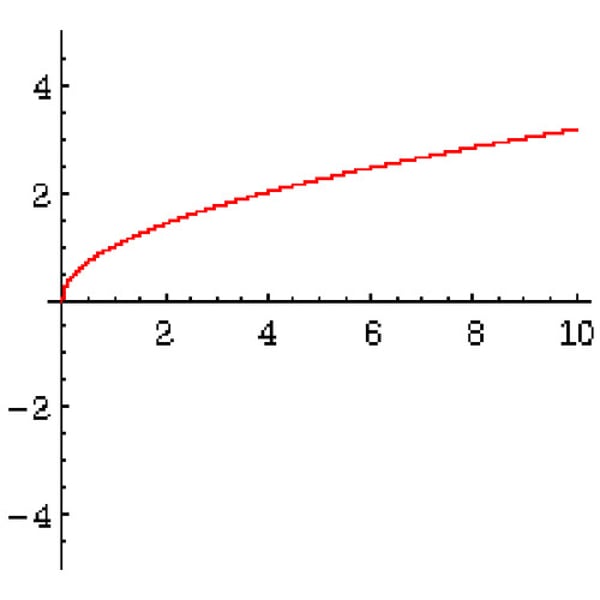
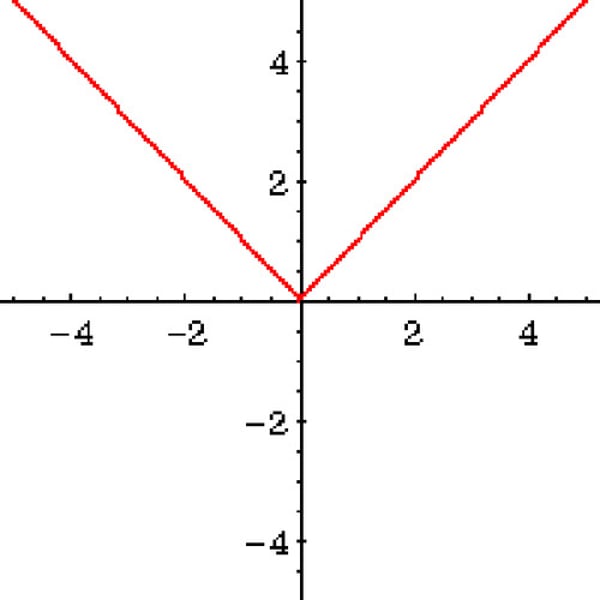
Absolute Value Function

y=a|x-h|+k (even func symmetry over y-axis)

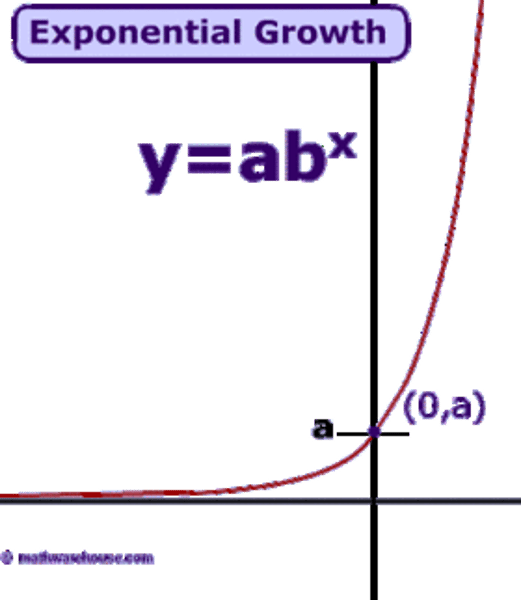
Exponential Growth or Decay Formula

y=ab^x

logarithmic function

y= logbase b (x)

y= log(x-x)+y

negative w x reflects over y-axis

negative in front reflects over x-axis

rational functions

ax^m +….

/ bx^n + …

polynomial/polynomial

1. factor

2. infinite discontinuity: denom to 0 (vertical asymptote)

3. removable discontinuity: cancel out, set to 0, plug back in

4. end behavior asymptote (horizontal): to what power / coeff

   1. m=n → y=a/b

   2. m < n y=0

   3. m > n slanted asymptote: polynomial long division (numerator degree is 1 higher)

5. x-int set equation to 0

6. y-int make x 0

if there are 2 vertical asymptotes/infinite asymptotes check for?

crossing: set equation equal to horizontal asymptote & if you get a # it crosses!