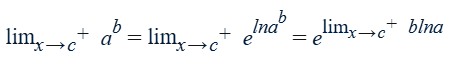Unit 1 Calculus 2

∫ tanx dx

ln|secx|

∫ cotx dx

ln|sinx|

∫ secx dx

ln|secx + tanx|

∫ cscx dx

-ln|cscx + cotx|

Domain/range restriction for sinθ = x / sin^-1x = θ

interval: -π/2 ≤ θ ≤ π/2

Unit Circle: Q4 and Q1

Domain/range restriction for tanθ = x / tan^-1x = θ

interval: -π/2 < θ < π/2

Unit Circle: Q4 and Q1

Domain/range restriction for cosθ = x / cos^-1x = θ

interval: 0 ≤ θ ≤ π

Unit Circle: Q1 and Q2

Domain/range restriction for secθ = x / sec^-1x = θ

interval: θ ∈ [0,π/2) U [π,3π/2)

Unit Circle: Q1 and Q3

How to find the exact value of an inverse function

1. Let f^-1(a) = θ, so f(θ) = a

2. Locate θ on the Unit Circle, keeping in mind the restrictions

How to simplify g(f^-1(a))

1. Let f^-1(a) = θ

2. Put f(θ) = a on a right triangle

3. Find g(θ)

* A leg can be negative depending on the quadrant of the Unit Circle, but the hypotenuse is always positive.

Graph of tan^-1(x)

• tan^-1(0) = 0

• tan^-1(+∞) = π/2

• tan^-1(-∞) = -π/2

d/dx sin^-1x

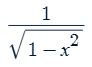
d/dx cos^-1x

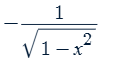
d/dx tan^-1x

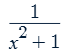
d/dx cot^-1x

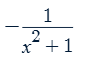
d/dx sec^-1x

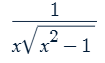
d/dx csc^-1x

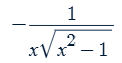
Deriving inverse function f^-1(x) by implicit differentiation

1. Let f^-1(x) = y, so f(y) = x

2. d/dx [f(y) = x]

3. Solve for dy/dx

4. Use the Pythagorean identities to get f(y)

5. Substitute x for f(y)

6. d/dx [f^-1(x) = y] to get d/dx [f^-1(x)] = dy/dx

7. Replace dy/dx with the expression in terms of x found

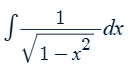
sin^-1x

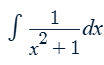
tan^-1x

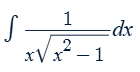
sec^-1x

Integration by parts formula

indefinite integral: ∫udv = uv − ∫vdu

Tips

• What’s easy to derive is u. What’s easy to integrate is dv.

• Choose the x with the highest power to be u.

• Sometimes substitution is needed to set up ∫udv.

• If you end up with the original integral, combine them and divide everything by the coefficient.

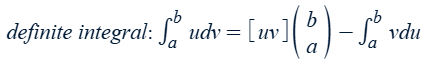
∫ sin^m(x)cosⁿ(x) dx

n ≥ 1 and odd, and u-substitution does not work

1. Factor out cosx and the remaining even cosx’s into cos²x’s

2. Substitute cos²x = 1 − sin²x

3. u = sinx, du = cosx dx (replaces the factored cosx)

∫ sin^m(x)cosⁿ(x) dx

m ≥ 1 and odd, and u-substitution does not work

1. Factor out sinx and the remaining even sinx’s into sin²x’s

2. Substitute sin²x = 1 − cos²x

3. u = cosx, du = -sinx dx (replaces the factored sinx)

∫ sin^m(x)cosⁿ(x) dx

n and m are even, and u-substitution does not work

1. Factor into sin²x’s and cos²x’s

2. Substitute:

• sin²x = ½ (1 − cos2x)

• cos²x = ½ (1 + cos2x)

∫ tan^m(x)secⁿ(x) dx

n ≥ 2 and even, and u-substitution may not work

1. Factor out sec²x and the remaining even secx’s into sec²x’s

2. Substitute sec²x = tan²x + 1

3. u = tanx, du = sec²x dx (replaces the factored sec²x)

∫ tan^m(x)secⁿ(x) dx

n, m ≥ 1, m is odd, and u-substitution does not work

1. Factor out secxtanx and the remaining even tanx’s into tan²x’s

2. Substitute tan²x = sec²x − 1

3. u = secx, du = secxtanx dx (replaces the factored secxtanx)

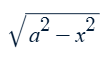
1. Substitute x = asinθ and

   dx = acosθ dθ

   √(a² − (asinθ)²)

   √(a² − a²sin²θ)

2. Factor out a²

   √(a²(1 − sin²θ))

   a√(1 − sin²θ)

3. Substitute 1 − sin²θ = cos²θ

   a√cos²θ

   acosθ

4. Convert from terms of θ to x using a right triangle, knowing that sinθ = x/a and θ = sin^-1(x/a)

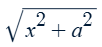
1. Substitute x = atanθ and

   dx = asec²θ dθ

   √((atanθ)² + a²)

   √(a²tan²θ + a²)

2. Factor out a²

   √(a²(tan²θ + 1))

   a√(tan²θ + 1)

3. Substitute tan²θ + 1 = sec²θ

   a√sec²θ

   asecθ

4. Convert from terms of θ to x using a right triangle, knowing that tanθ = x/a and θ = tan^-1(x/a)

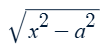
1. Substitute x = asecθ and

   dx = secθtanθ dθ

   √((asecθ)² − a²)

   √(a²sec²θ − a²)

2. Factor out a²

   √(a²(sec²θ − 1))

   a√(sec²θ − 1)

3. Substitute sec²θ − 1 = tan²θ

   a√tan²θ

   atanθ

4. Convert from terms of θ to x using a right triangle, knowing that secθ = x/a and θ = sec^-1(x/a)

Complete the square formula for

x² + bx + c

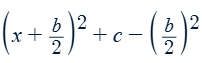
Double angle formula

sin(2x) = 2sinxcosx

numerator degree ≥ denominator degree

Use long division to simplify the integrand.

numerator degree < denominator degree

1. Factor the denominator, if needed.

2. Decompose the integrand into partial fractions with unknown constants for numerators.

3. Combine fractions using a common denominator that’s the same as the original denominator.

4. Set the new numerator equal to the original.

5. Solve for the constants by inserting eliminatory x-values and/or creating equations from coefficients.

The denominator has distinct linear factors:

(a₁x + b₁) (a₂x + b₂) … (a_nx + b_n)

* x is a linear factor

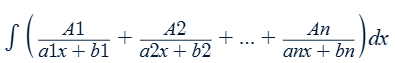
The denominator has a repeated linear factor:

(ax + b)ⁿ

* xⁿ is a repeated linear factor

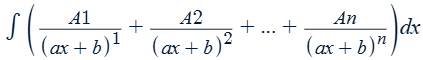
The denominator has a distinct irreducible factor:

ax² + bx + c (bx may be missing because b = 0)

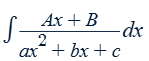
The denominator has a repeated irreducible factor:

(ax² + bx + c)ⁿ (bx may be missing because b = 0)

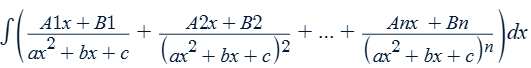
How to rationalize a function with a square root containing x¹ in the denominator using u-substitution

1. Let u equal the square root

   ex. u = √x

2. Find u² to cancel out the radical

   u² = (√x)²

   u² = x

3. Derive u²

   2u du = 1dx

4. Substitute

Integral with respect to x for the area between two curves

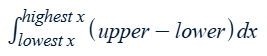
Integral with respect to y for the area between two curves

Integral for the volume of a solid...

• without a hole

• revolved around a horizontal axis (y = a)

Disk method with respect to x

* One function is the axis of revolution, a.

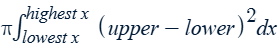
Integral for the volume of a solid…

• without a hole

• revolved around a vertical axis (x = a)

Disk method with respect to y

* One function is the axis of revolution, a.

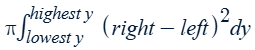
Integral for the volume of a solid…

• with a hole

• revolved around a horizontal axis (y = a)

Washer method with respect to x

* Each radius is upper − lower, where one function is the axis of rotation, a

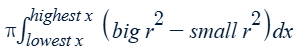
Integral for the volume of a solid…

• with a hole

• revolved around a vertical axis (x = a)

Washer method with respect to y

* Each radius is right − left, where one function is the axis of rotation, a

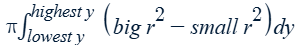
L’Hôpital’s rule

Conditions: f(a)/g(a) = 0/0 or ∞/∞ (indeterminate form, NOT 1)

Tips

• Can be performed as many times as needed and with higher-order derivatives

• Create one fraction by taking reciprocals and substituting trig identities.

• The limit of a constant is that very constant.

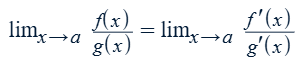
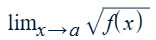
How to break out the radicand

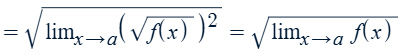
Limit chain rule