103 math preparation

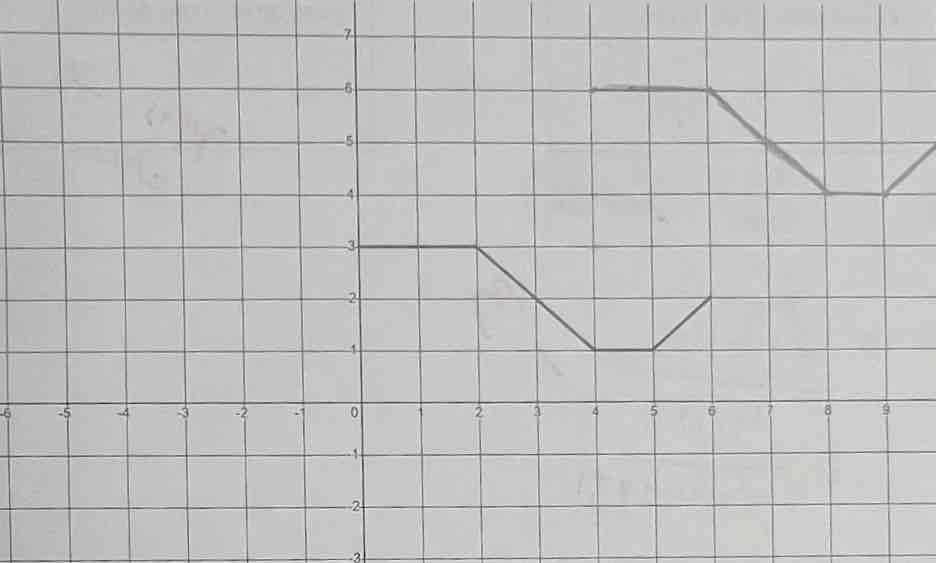
The graph of the function y = f(x) is shown below. On the same coordinate plane, draw

the graph of

f(x - 4) + 3

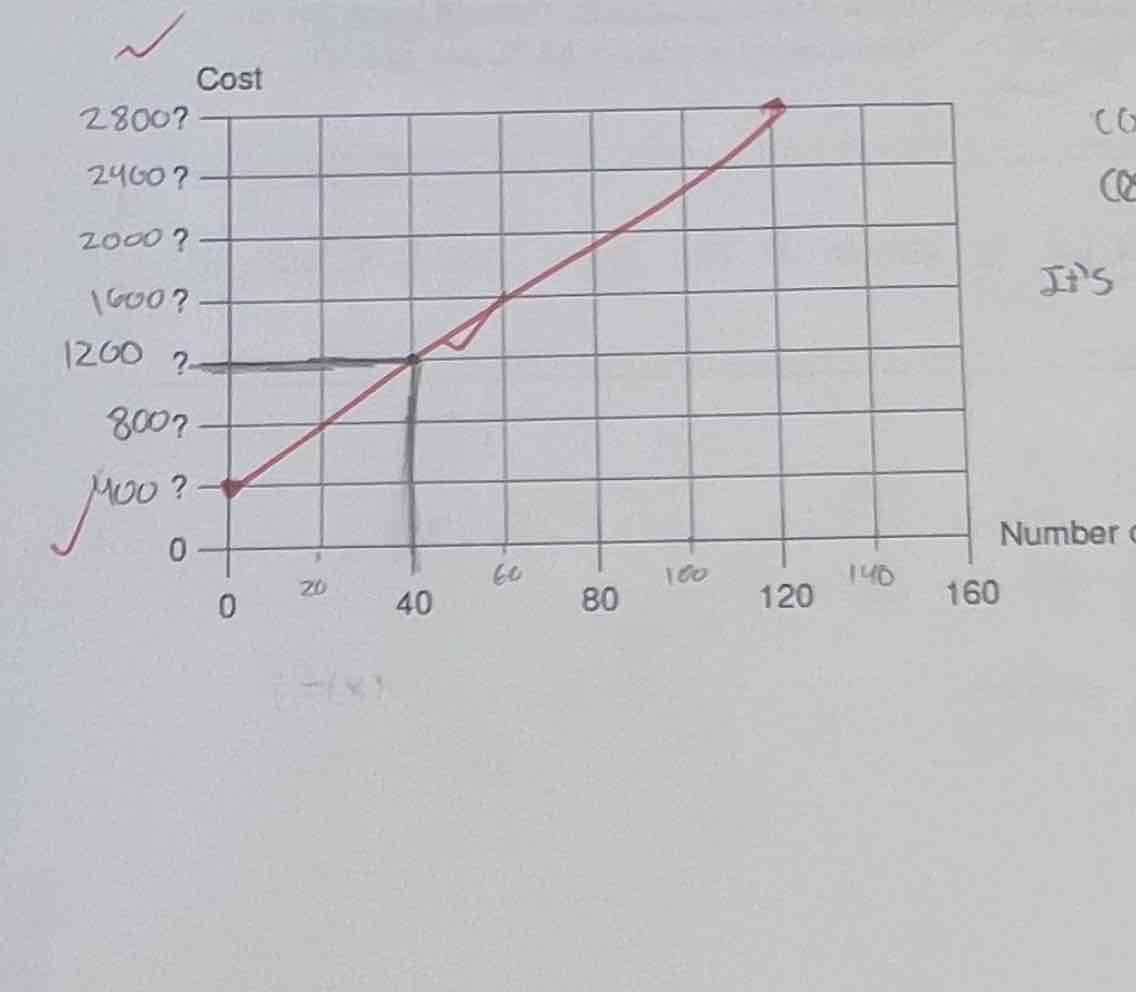
The cost (in dollars) to produce x flower pots is C (x) = 400 + 20x. So it costs $1200 to produce 40 flower pots. This point is shown on the graph paper below. Draw an accurate graph of the cost function, C(x). Label the ticks on the cost-axis.

C(x)=400+20 (60) = 1600

Cx）=400+20180-2000

It's going up by $400

The demand for heating oil depends somewhat on the average temperature outside. The average monthly demand for heating oil when the average temperature is 24° is 150 gallons. The average monthly demands for heating oil when the average temperature is 44° is 100 gallons. Use linear interpolation to estimate the average demand for heating oil when the average temperature is 36°.

Here 44° becomes x1 100 becomes y1

24° become x2 and 150 becomes y2

Then you subtract x1 & x2 Over y1 - y2

Redink Publishing Company is producing and selling a textbook for Math 103. The fixed costs are $2800 and it costs $40 per copy to print it. The price-demand equation is p =101 - 0.03x, where x is the number of books that can b sold at a price of p dollars,

A) Write a formula for the cost function to produce x books.

B)Write an expression R(x) for revenue as a function of x.

C)Let P(3) be profit in dollars as a function of x books sold. Find P(100)

A)C(x) = 2800 + 40 (x)

B) R(x) = x(101 - 0.03x)

C) p(x)=R(x)-C(x)

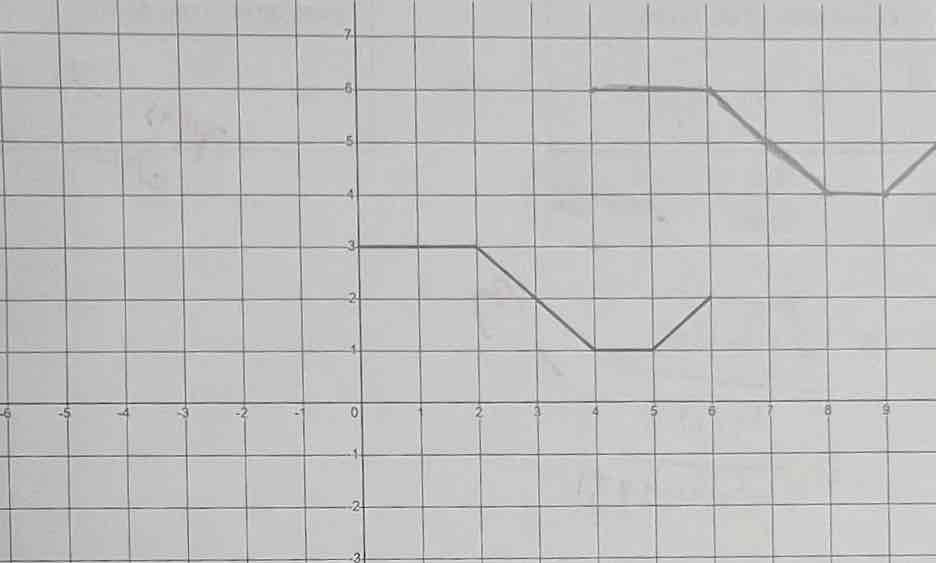
The graph of the function y = f(x) is shown below. On the same coordinate plane, draw

the graph of

f(x - 4) + 3

All you do here is move 4 to the right and 3 up

The fixed daily cost to run a gold mine is $2200. In addition, it costs $40 per pound of gold ore mined. Find the formula for the average cost function C(x). C(x) is the average daily cost per pound of ore if x pounds are mined.

C^-(x) = 2200+40(X) over x

If the cost function in dollars is C(x) = 300 + 5x then the per item cost is 5 dollars. True or false?

True

The slope of the price demand function 0.4 + 4p = 70 is positive. True or false

False

For the function f(x) = x2 + 4x → f(1) = 10 True or false?

False

The revenue function is equal to the price per item times the number of items sold. True or false?

True

The break-even points happen when revenue equals cost. True or false

True

The fixed daily cost to run a gold mine is $2000. In addition, it costs $35 per pound of gold ore mined.

a. Find the formula for the cost function C(x). C (x) is the daily cost per pound of ore if x pounds are mined.

b. Find the formula for the average cost function C^-(x). C^-(x) is the average daily cost per pound of ore if x pounds are mined.

C.Find im C^ (x).

A.C(x) = 2000+35 (X)

B.C^-(x)=2000+ 35(X) over x

C. C^-=35

Usage for electricity is measured in kilowatt hours (K WH), There is a base charge of $9.00. The cost for the first 300 (or fewer) KWHS is $0.20 per KWH. The cost for K WH over 300 is $0.15 per KWH.

Find a formula for the cost function, K(x), for using x KWH if x is greater than 300.

Formula for the cost if x is greater than 300:

K(x)= 9.00+0. 20(300)+0.15(x-300)

This is 9 is the base price the 0.20 is per kWh and the 300 is how much they used.

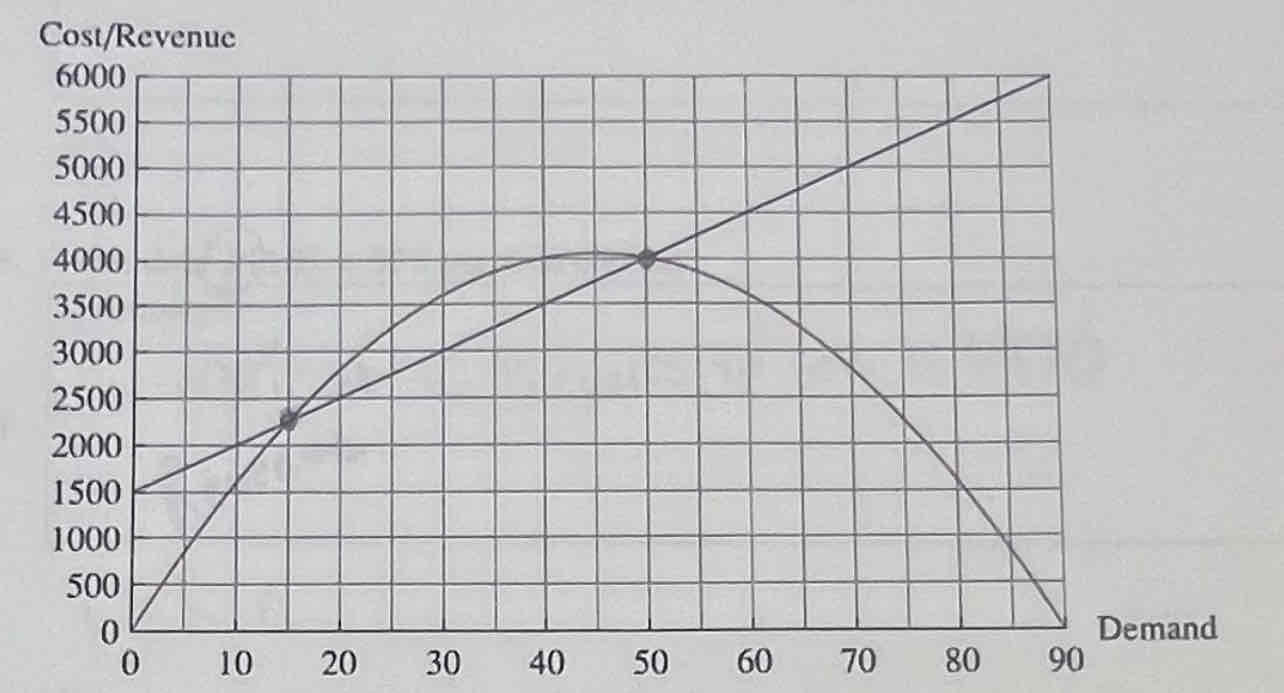
3. The revenue from selling & maple-wood picture frames is

R(x) = (180 - 2x)x

The cost function is C(x) = 50x + 1500. The revenue and the cost are in dollars; their

graphs are shown below:

A) Fill in the blanks: If the number of picture frames produced and sold is between ___ and ___The company will make profit.

B) b. If the number of picture frames produced and sold is less than___ or more than ___ they will have a lost.

C)Find the profit function.

A) Fill in the blanks: If the number of picture frames produced and sold is between 15 and 50 The company will make profit.

B) b. If the number of picture frames produced and sold is less than 15 or more than 50 they will have a lost.

C)P(x)= - 2x²-130x-1500

Solve the following system of equations by triangularization:

4х - 2y= 8

-3х-5y = -6

all you do here is multiply the first variable in front x in row 1 with row 2 and the opposite for row 2.

Then you simplify so it would become -26y=0

Bc you add the 6y and the 20y = 0 because 24-24 =0 then put zero into 4х - 2y= 8 and make 4х - 2(0)= 8 which becomes 4x=8 and 8 is the answer

The supply and demand equations for a product are given below:

supply q + 3p = 5

demand 4g + 2p = -10

q is the number of items the supplier will produce if the price is p dollars. q is also the number of items the consumer will buy if the price is p dollars. Find the equilibrium values of q and p. Solve for p, and g.

P=

Q=-4

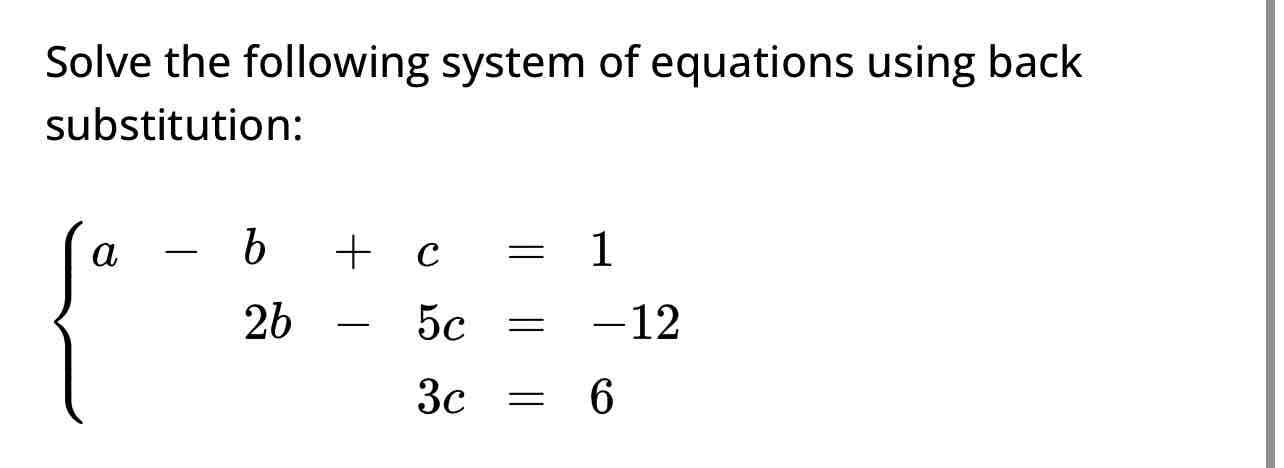
Solve the following system of equations using back substitution:

A=b+c=1

2b+5c=-12

3c=6

A=-2

B=-1

C=-2

what you do here is solve from the bottom first and then go up and plug them into the equation

The price-demand equation for Parilla Pasta is 3x + 350p = 4000, where p is the

price per pound and x is the weekly demand measured in pounds.

A) writ the demand x as a function of price

For price demand you subtract the number infront of p than move to the other side and then divide by the number infront of x

The price-demand equation for Parilla Pasta is 3x + 350p = 4000, where p is the

price per pound and x is the weekly demand measured in pounds.

b) find the demand when the price is $2.00 per pound. Be sure to include the proper units in your statement.

you continue of from step one which is subtract or add move to the other side and divide. At that step you plug in the $2.00 and multiply the 350 then subtract the what’s infront and then divide

The price-demand equation for Parilla Pasta is 3x + 350p = 4000, where p is the

price per pound and x is the weekly demand measured in pounds.

Write the revenue R(p) as a function of price.

I This becomes the same things as the first ones but So it become R(p)=(4000-350p)/3

And then you multiply everything times p except the bottom you subtract that.

So it becomes R(p)=(4000p-350p²)3-400

What is price demand? How does it look

Price demand is pretty much when you subtract or add the number infront of p in order to move it to the other side then divide by what’s infront of x

The price-demand equation for Parilla Pasta is 6x + 7p = 800, where p is the price

per pound and x is the weekly demand measured in hundreds of pounds.

Frost Cream can sell 20 cones when the price is $3.50 per cone. When the price is $1.50 per cone they can sell 40 cones.

a. What is the average rate of change in price between 20 and 40 cones.

You subtract the $1.50 from the $3.50 and 20 cones from the 40 cones

You get $2.0over 20 And divide which become .10¢ per cone

Frost Cream can sell 20 cones when the price is $3.50 per cone. When the price is $1.50 per cone they can sell 40 cones.

B. Use the linear interpolation to estimate the price if 25 cones are sold

You plug it into the slope($1.50-$3.50)/40-20)

Which becomes -$2.00/20

Then that becomes $-0.10

Which becomes y - 3.50 = -0.10(25 - 20)

y - 3.50 = -0.10(5)

y - 3.50 = -0.50

y = -0.50 + 3.50

y = $3.00

What is r(p) as a function of price

I This when the you multiple everything by p