Math 118 Quiz 2
0.0(0)
0.0(0)
Card Sorting
1/59
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
60 Terms
1
New cards
Area of a circle
A\=πr²
2
New cards
Area of a rectangle
A\=lw
3
New cards
Area of a triangle
A\=1/2bh
4
New cards
Volume of a cylinder
V\=πr²h
5
New cards
Volume of a rectangular solid
V\=lwh
6
New cards
Volume of a triangular prism
V\=(1/2bh)h
7
New cards
Circumference of a circle
C\=2πr
8
New cards
Even symmetry: if \_____, then \_____
if (a,b), then (-a, b)
9
New cards
Odd symmetry: If \_____, then \_____
if (a,b), then (-a,-b)
10
New cards
Symmetric about the line y\=x: If \_____, then \_____
If (a,b), then (b,a)
11
New cards
What are the domain restrictions for a log function?
x \> 0
12
New cards
List the asymptotes for y\=2^x
horizontal
13
New cards
General equation for a vertical shift
f(x) + c
14
New cards
How do you demonstrate a vertical shift on a set of points?
Either add or subtract c from the y-values
15
New cards
General equation for a vertical stretch/compression
cf(x)
16
New cards
When is cf(x) a vertical stretch?
when c is greater than one
17
New cards
When is cf(x) a vertical compression?
when c is greater than zero, but less than one
18
New cards
How do you demonstrate a vertical stretch on a set of points?
multiply y values by c
19
New cards
How do you demonstrate a vertical compression on a set of points?
divide y values by c
20
New cards
General equation for horizontal shift
f(x+c)
21
New cards
How do you demonstrate a horizontal shift on a set of points?
Either add or subtract c from the x-values
22
New cards
If c is positive during a horizontal shift, do you add or subtract c from the x-values?
subtract
23
New cards
If c is negative during a horizontal shift, do you add or subtract c from the x-values?
add
24
New cards
General equation for a horizontal compression/stretch
f(cx)
25
New cards
When is f(cx) a compression?
when c is greater than one
26
New cards
When is f(cx) a stretch?
when c is greater than one but less than zero
27
New cards
How do you demonstrate a horizontal stretch on a set of points?
multiply x-values by the reciprocal of c
28
New cards
How do you demonstrate a horizontal compression on a set of points?
divide x-values by c
29
New cards
What is -f(x)?
vertical flip, reflection about the x-axis
30
New cards
How do the points of a function change when there is a vertical flip/reflection about the x-axis?
x remains unchanged, y switches signs
31
New cards
What is f(-x)?
horizontal flip, reflection about the y-axis
32
New cards
How do the points of a function change when there is horizontal flip/reflection about the y-axis?
x switches signs, y remains unchanged
33
New cards
What must you do if you have a horizontal shift and another horizontal transformation?
factor the argument to see the true shift
34
New cards
Steps for a sequence of transformation
1. horizontal stretch/compression
2. horizontal shift
3. vertical flip
4. vertical stretch/compression
5. horizontal flip
6. vertical shift
35
New cards
Recursive model equation
Ysubt = (1+n)Ysub(t-1)
36
New cards
what is n?
the number of iterations
37
New cards
Explicit function equation
Ysubt = (1+n)^t\*ysubzero,
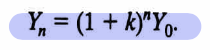
38
New cards
what can n be thought of as?
the independent variable
39
New cards
what can y be thought of as?
the dependent variable
40
New cards
when should you use recursive models?
discrete (not continuous)
41
New cards
when should you use explicit function?
with continuous
42
New cards
What should you do if an explicit function is used for a discrete-valued function?
restrict the domain
43
New cards
define variable for y=ab^x
y=0 is the horizontal asymptote, a is the initial amount, b is the growth factor, and x is the number of growth periods
44
New cards
describe b = 1 +r
the growth factor equals the growth rate plus one
45
New cards
what is asubn?
the future value of an initial deposit
46
New cards
compounding recursive formula?
Asubt=asub(t-1)\*(1+r/n)
47
New cards
compounding explicit formula?
A=Asubzero\*e^rt

48
New cards
e=_____?
(1+I/n)^n
49
New cards
What happens when interest is compounded more than once a year?
annual interest rate is divided by the number of compounding periods
50
New cards
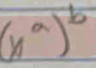
(x^a)^b = _____?
x^a\*b
51
New cards
Exponential graphs will contain what?
(0,1) (1,b) (-1, 1/b) and y=0
52
New cards
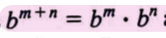
b^m+n=_____?
b^m+b^n
53
New cards
Exponential functions with a base between 0 and 1, or a negative coefficient model _____?
exponential decay
54
New cards
(a\*b)^n =______?
a^n\*a^b
55
New cards
(a^p)^q=______?
a^pq
56
New cards
a^-p
1/a^p
57
New cards
domain and range of y=b^x
domain: all real numbers, range y>0
58
New cards
horizontal stretches of compression can be modeled as ____?
a change of base
59
New cards
a horizontal shift can be modeled as?
a vertical stretch or compression
60
New cards
What is the annual percentage yield?
effective annual rate of return taking into account the effect of compounding interest.