Unsupervised Learning and PCA

Flashcards covering key concepts related to unsupervised learning, PCA, Hebbian learning, Oja's Rule and Sanger's Rule.

What is the main goal of unsupervised learning?

To discover hidden patterns or structure in unlabeled data.

Name two types of unsupervised learning.

Clustering and dimensionality reduction.

What does variance measure?

The spread of data around the mean.

What does covariance indicate?

How two variables change together.

What is the formula for correlation?

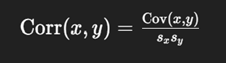
What is the main goal of PCA?

To reduce dimensionality while preserving the maximum variance.

What are the steps of PCA?

Center data → compute covariance matrix → find eigenvectors/eigenvalues → sort → project data.

What does the first principal component represent?

The direction of greatest variance in the data.

Are principal components correlated or uncorrelated?

Uncorrelated (orthogonal).

What is the key idea behind Hebbian learning?

"Neurons that fire together wire together" — strengthens weights between co-active units.

What is the Hebbian learning rule formula?

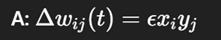
• Δw_ij = Change in weight between input neuron i and output neuron j

• ε (epsilon) = Learning rate controlling update speed

• x_i = Activation/value of input neuron i

• y_j = Activation/value of output neuron j

• Implements "neurons that fire together, wire together"

What’s the main drawback of Hebbian learning?

Weights grow infinitely without normalization.

Why is Hebbian learning called a "local" learning process?

Because weight updates depend only on information available at the synapse itself (input and output activity), with no need for global error signals.

Why is Hebbian learning called "correlational learning"?

It naturally detects and strengthens connections between correlated inputs and outputs, effectively encoding correlation patterns found in data.

What is Oja's rule and how does it modify Hebbian learning?

Oja's rule (Δwij = ε · yi · (xj - yi · wij)) adds a normalization term that prevents weights from growing unbounded.

What happens with a small learning rate (ε) in Hebbian learning?

More stable learning and noise resistance, but slow convergence and possible local minima problems.

What happens with a large learning rate (ε) in Hebbian learning?

Faster initial learning but potential instability, oscillations, overshooting, and risk of numerical overflow.

How do you interpret the values in a Hebbian weight vector?

Large positive weights indicate strong positive correlations, large negative weights indicate strong negative correlations, and weights near zero indicate minimal correlation.

What is Oja’s Rule ?

Normalized version of Hebbian learning that prevents weight explosion.

Ensures weights stay bounded.

What's the main problem with basic Hebbian learning?

Weights grow without bound (explode) if learning continues indefinitely, as there's no inherent mechanism to limit weight size.

What does Oja’s Rule learn?

The first principal component.

Write Oja’s Rule in update form.

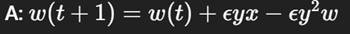
Does Oja’s Rule normalize weights?

Yes.

What is Sanger’s Rule used for?

Extension of Oja’s Rule to learn multiple principal components, not just the first.

Ensures each new component is orthogonal to the previous ones.

How does Sanger’s Rule ensure orthogonality?

By subtracting projections onto previously learned components.

Write the Sanger’s Rule formula.

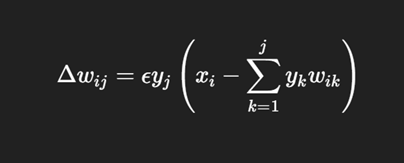
How is PCA used in image compression?

It reduces image dimensions by projecting onto top components, then reconstructs the image.