calc 4 - midterm 1 theorems
0.0(0)
Card Sorting
1/3
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
4 Terms
1
New cards
Green’s Theorem
counterclockwise - negative
clockwise - positive
C is positively oriented, piecewise smooth, simple closed curve
D is the region bounded by C
F must have continuous partial derivatives on an open region containing D
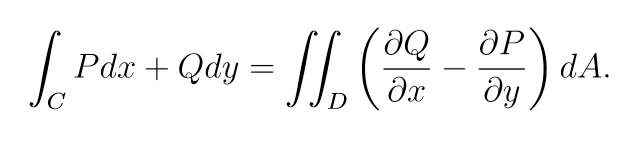
2
New cards
Stoke’s Theorem
S is oriented, piecewise smooth surface bounded by C
C is positively oriented
F has continuous partial derivatives on and around S
(S is the surface, D is the domain that defines S)
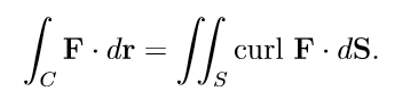
3
New cards
Divergence Theorem
“flux”
E is a simple solid region
S is the closed surface that bounds E, oriented outwards (pos)
F has continuous partial derivatives on an open region containing E
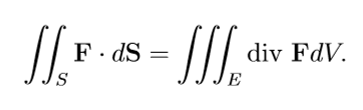
4
New cards
x
x