ELASTIC COLLISIONS IN 2 DIMENSIONS - CH5

when a particle collides with a smooth flat surface, where does the impulse act?

perpendicular to the surface

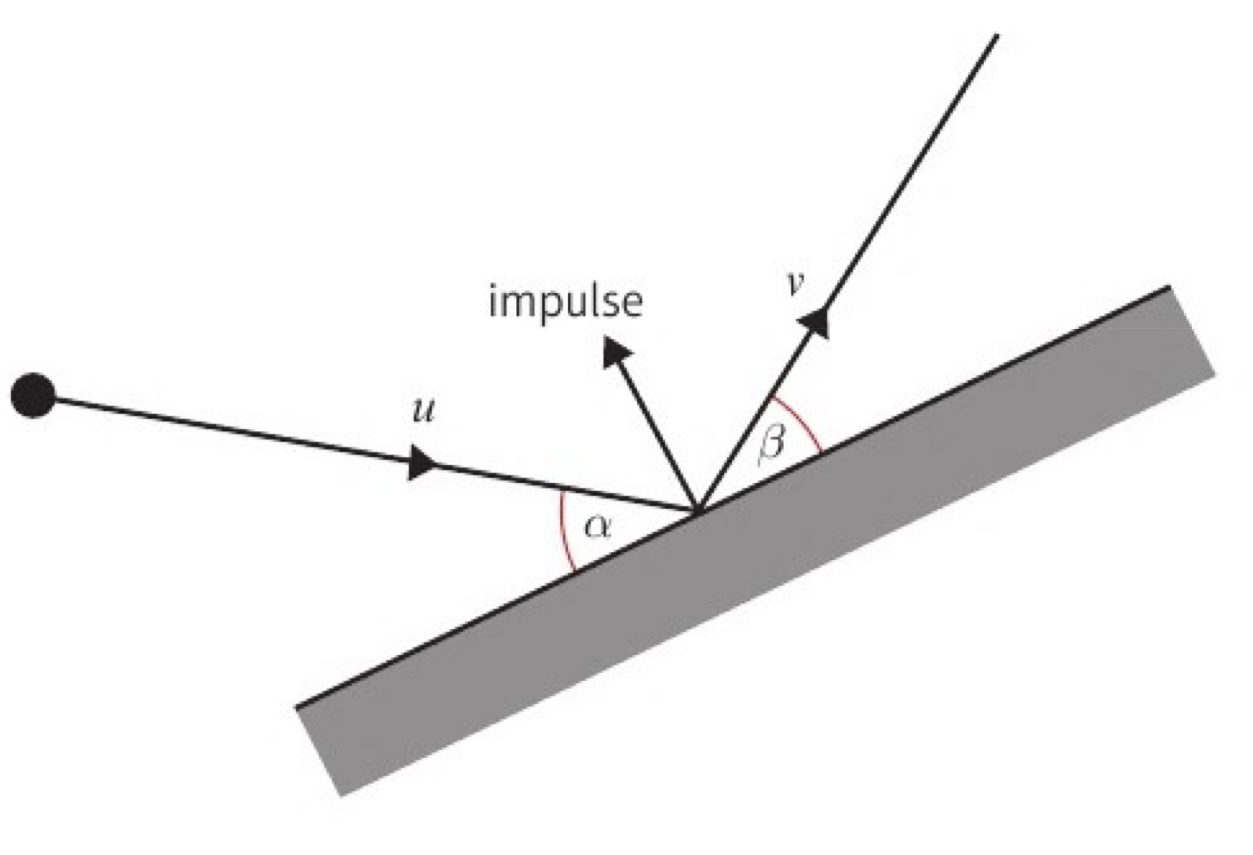
what are the components of velocity of the particle

• the velocity parallel to the surface is unchanged: vcosß = ucosα

• the velocity perpendicular to the surface can be calculated with Newton’s law of restitution: vsinß = eusinα

after eliminating u and v from the above equation, what do you get?

tanß = etanα

what’s the angle of deflection?

the total angle by which the angle of the sphere changes, i.e. α + ß

successive collisions

kind of the same for with one dimension? solve the first one normally, then substitute in the final v from collision 1 into an initial velocity from collision 2. use trig to find angles, they’ll usually form triangles.

what must you watch out for with successive collisions

sometimes e won’r be the same for both surfaces!!!

when two spheres collide, where does impulse act?

along the line of centres, i.e. the line connecting the centres of the two spheres

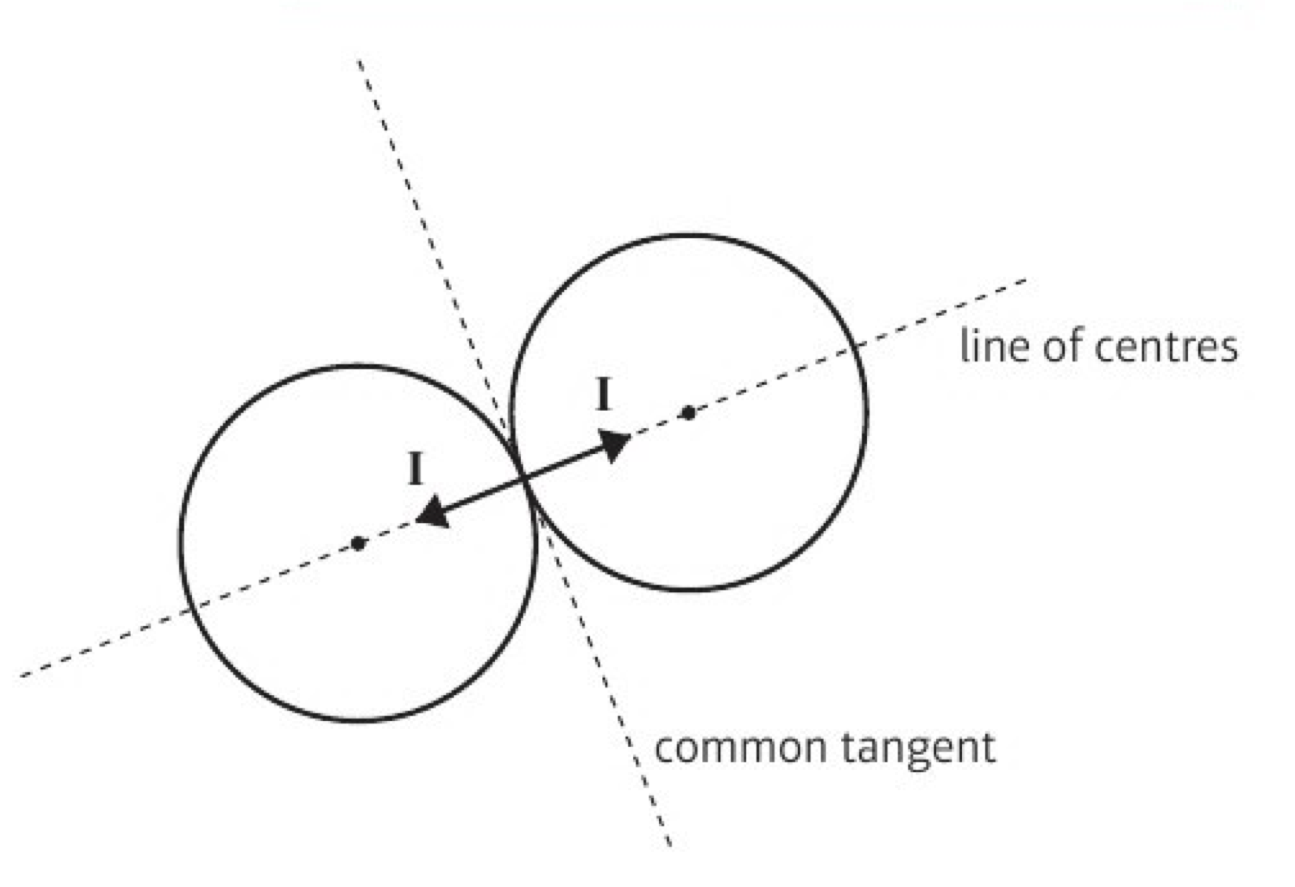
what are the components of the velocities after the collision?

• perpendicular to the line of centres is unchanged

• the component parallel to the line will have to be calculated using conservation of momentum