Statistical Modelling

cries

Var(AY+b)

A (sigma) A^T

Least Squares Estimates

Beta_hat = (X^TX)^-1X^Ty

Fitted Values

XB_hat = X(X^TX)^-1X^Ty

Unbiased Linear Estimator for Lamba

var(a^TY) >= var(Lamba^Teta)

iff a = X(X^TX)^-1X^TLamba

Confidence Interval for B_j

B_hat_j +- t(alpha/2) * Standard Error * sqrt(c_jj)

Confidence Interval for eta₀

add 1+ to the sqrt for the prediction interval

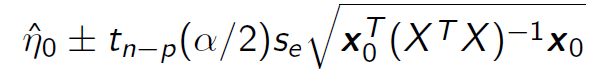
Leverage

OR for an mxn matrix => n/m
OR 1/n + (x_i-x_bar)² / sum (x_i-x_bar)²

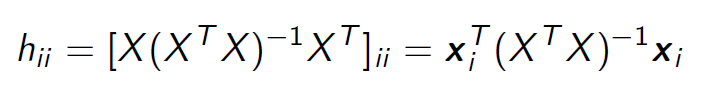
Cook’s Distance

B_hat for GLS

(X^TV^-1X)^-1X^TV^-1Y

Var(B_hat) for GLS

sigma² (X^TV^-1X)^-1

Weighted Least Squares

w_i = 1/v_i

Box Cox Transformation

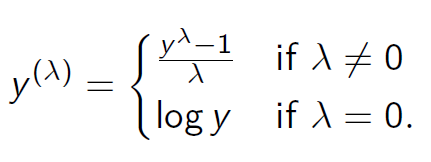
Inverse Box Cox Transformation

for lamba ≠ 0 => lamba*y + 1
for lamba = 0 => exp(y)

pi_i

exp(eta) / (1 + exp(eta))

eta

log(pi_i/(1-pi_i)) = logit(pi_i) = B₀+B₁x

Log-Likelihood Function

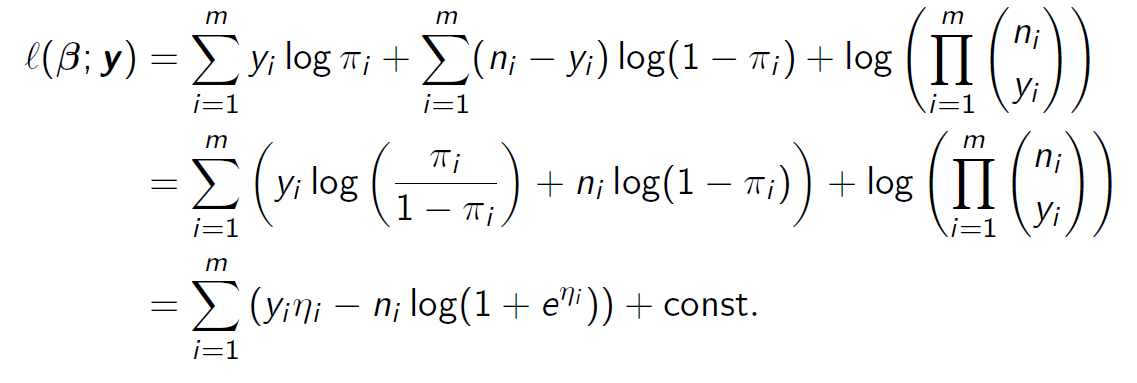
Fisher Information Matrix

Var(S(B)) = I(B)
= Var(X^T(Y - mu))
= X^TVar(Y) X

= X^TDX

Where S(B) = X^T(Y-mu)

Newton - Raphson Algorithm

B^(t+1) = B^(t) - [S’(B^(t))]^-1S(B^(t))

where S’(B^(t)) = partial derivative of Sj wrt B_k

= partial derivate squared L/BjB_k

Fisher Scoring

B^(t+1) = B^(t) + [I(B^(t))]^-1 + S(B^(t))

= B^(t) + (X^TD^(t)X)^-1 X^T(y-mu^(t))

where mu^(t) = n_ipi_i and D^(t) = diag(n_ipi_i(1-pi_i))

B⁽⁰⁾

B⁽⁰⁾ = (X^TX)^-1X^Tv

where v = log[(y_i + 0.5)/(n_i - y_i + 0.5)]

Confidence Interval for Bj

B_hat_j +- z(alpha/2) sqrt( [I(B)^-1]_jj )

Log Likelihood Ratio Test Statistic

G² = 2( L(B_hat) - L(B_hat₀) )

Null Deviance

2 ( L(Saturated) - L(Null) )

Residual Deviance

2 ( L(Saturated) - L(Residual) )

Overdispersion

Var(Y_i) > n_ipi_i (1-pi_i)

Underdispersed => Var(Y_i) < n_ipi_i (1-pi_i)

Properly dispersed/fine => Var(Y_i) = n_ipi_i (1-pi_i)

Log Odds Ratio

B_i = log ( (pi₂/(1-pi₂)) / (pi₁/(1-pi₁)) )

= logit(pi₂) - logit(pi₁) = B₂ - B₁

Increasing x_i by 1 - Poisson

Y’_i = exp(B_hat₁) * Y_i

Predict Y for Poisson Regression

Y = exp(B₀ + B₁x)

Predict Y for Poisson Rate Regression

Y = offset * exp(B₀ + B₁x)

Root Mean Square Error (RMSE)

sqrt( 1/n + sum( y_i - f(x_i) ) ² )

R²

cor( y , f(x) )²

= (TSS-RSS) / TSS = 1 - RSS/Tss

= 1 - sum( yi - f(x) )² / sum ( y_i - y_bar )²

Adjusted R²

1 - ( RSS / (n-k-1) ) / (TSS / (n-1) )

C_p

1/n (RSS + 2k(sigma)²)

Mallow’s C’_p

RSS/(sigma)² + 2k - n

AIC (Akaike Information Criterion)

2k - 2 ln (L)

AICc (Akaike Information Criterion Corrected)

AIC + [ 2k (k+1) / (n - k - 1) ]

BIC (Bayesian Information Criterion)

ln(n)k - 2 ln(L)

Cross Validation Estimate

sum [ n_k /n MSE_k]

where MSE_k = (y_i - y_hat_i)² / n_k

Mean Absolute Error

1/n sum |y_i - f(x_i)|

Point Prediction

B₀ + B₁x + …