The mathematics of patterns and symmetries

A _____________________ is a repeated arrangement of numbers, shapes, colors and so on It can be related to any type of event or object

Pattern

If the set of numbers are related to each other in a specific rule, the the rule or manner is called a ____________

pattern

Sometimes, patterns are also known as a ___________

sequence

Patterns are ________ or ________ in numbers

finite
infinite

A _____________________ is a regularity in the world, in human-made design, or in abstract ideas

pattern

The elements of a pattern repeat in a ____________ manner

predictable

A _____________ is a kind of pattern formed of geometric shapes and typically repeated like a wallpaper design

Geometric pattern

Any of the senses may directly observe ____________

patterns

__________________ is defined as one shape is EXACTLY LIKE THE OTHER SHAPE when it is moved, rotated, or flipped

Symmetry

_______________ in everyday language refers to a sense of harmonious and beautiful proportion and balance

Symmetry

In mathematics, ____________ has a more precise definition, and is usually used to refer to an object that is invariant under some transformations including translation, reflection, rotation, or scaling.

Symmetry

According to Grunbaum and Shephard, a motif is “__________________”

any non-empty plane set

Any object drawn in a plane is a ____________

motif

A ______________ can be described as repetitions of a motif in the plane

pattern

An ___________________ is the rotation of a motif in a fixed angle about a fixed point.

Isometry

Each rotation of a figure is an _____________

isometry

The image of the basic motif under the additional number of rotation is a _____________

pattern

A ______________ changes the SIZE, SHAPE or POSITION of a figure and creates a new figure

Transformation

A ____________________ is either RIGID or NON-RIGID; another word for a rigid transformation is ISOMETRY

Geometry transformation

An ____________________ such as rotation, translation, or reflection, DOES NOT change the size or shape of the figure

Isometry

A _______________ is not an isometry since it either SHRINKS or ENLARGES a figure

dilation

What are the 4 types of transformation?

1. -

2. -

3. -

4. -

Translation
Reflection
Rotation
Dilation

The initial object to be transformed is called ___________

pre-image

The transformed object is called ___________

image

___________________ is a mathematical term used in geometry to describe a function that moves an object a certain distance. The object is not altered in any other way

Translation

___________________ is a transformation in which the figure or object is mirror image of the other

Reflection

_______________ is a transformation that turns a figure about a fixed point called the CENTER OF ROTATION. It can be done clockwise or counterclockwise

Rotation

Rotation is a transformation that turns a figure about a fixed point called the __________________

Center of rotation

A ________________ is a transformation that changes the size of a figure. It can become smaller or larger, but the shape remains the same

Dilation

____________________ is the combination of translation and reflectoin

Glided reflection

The name ____________________ is attributed to John Conway, an English mathematician who is active in finite theory, knot theory, number theory, combinatorial game theory, and coding theory.

Frieze patterns

The name Frieze patterns is attributed to ____________, an English mathematician who is active in finite theory, knot theory, number theory, combinatorial game theory, and coding theory.

John Conway

________________ are patterns that REPEAT IN A STRAIGHT VERTICAL or HORIZONTAL LINE. There are found in architecture, fabrics, and wallpaper borders, just to name a few

Frieze patterns

What are the 7 types of Frieze Patterns?

1. -

2. -

3. -

4. -

5. -

6. -

7. -

Hop
Step
Slide
Spinning Hop

Spinning sidle
Jump
Spinning jump

____________ is a pattern which only involves translation

Hop

_______________ is a combination of TRANSLATION and REFLECTION. It is also called GLIDE REFLECTION SYMMETRY

Step

________________ consists of TRANSLATION and VERTICAL REFLECTION symmetries

Slide

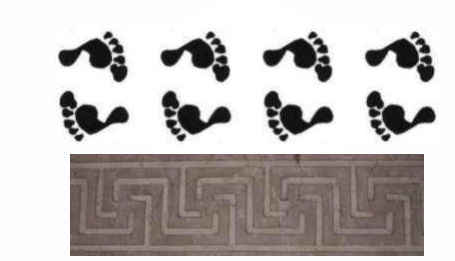
________________ contains TRANSLATION and ROTATION (by half turn or rotation at 180 degrees angle) symmetries

Spinning hop

_______________ contains TRANSLATION, GLIDE, REFLECTION and ROTATION (by a half-turn or rotation at 180 degrees angle) symmetries

Spinning sidle

_____________________ contains TRANSLATION and HORIZONTAL REFLECTION symmetries

Jump

_______________ contains ALL SYMMETRIES (translation, horizontal and vertical reflection, and rotation)

Spinning jump

If translation symmetry is added in a second, independent direction, one gets _______________. It turns out there are only ____ different wallpaper groups. 

wallpaper groups 
17

______________ comes from a greek word symmetria meaning TO MEASURE TOGETHER and is widely used in the study of geometry

Symmetry

Symmetry comes from a greek word __________ meaning ________________ and is widely used in the study of geometry

symmetria
to measure together

Mathematically, ___________________ means that one shape becomes exactly like another when you move it in some way: turn, flip, or slide

Symmetry

Not all objects have symmetry; if an object is not symmetrical, it is called _____________

asymmetric

Symmetry and pattern is widely used in fields of ____________ and _____________, it also appears in ________ and ______________

mathematics
arts
chemistry
biology

The __________________ for example is widely known to be symmetrical in nature

human anatomy

What are the 2 kinds of symmetry?

1. -

2. -

Bilateral symmetry
Radial symmetry

___________________ in which an object has two sides that are MIRROR IMAGES of each other

Bilateral symmetry

__________________, this is where a center point and numerous lines of symmetry could be drawn. One good example is the SPIDER WEB.

Radial symmetry

In the field of medical science, ______________ is the basis to detect anomalies in human bodies like disfigured parts of the body wherein one part being larger or smaller than its counterpart

Radial symmetry

Patterns in living things are explained by the biological processes of __________ and __________ selection

natural
sexual

One good example of patterns found in nature is the ______________________. Under favorable conditions, it doubles at regular intervals: 1, 2, 4, 8 or 2^n

bacterial population growth

_________________ is a pattern covering a place by fitting together replicas of the same basic shape

Tessellation

The word Tessellation comes from the Latin word “__________”, which means A SQUARE TABLET or die used in gambling.

Tessera

What are the 3 types of tessellation?

1. -

2. -

3. -

Regular Tessellation
Semi-Regular Tessellation
Demi-Regular Tessellation

A ______________ is made up of congruent REGULAR POLYGONS

Regular tessellation

_______________________ is also known as ARCHIMEDEAN tessellations and are regular tessellations of TWO OR MORE DIFFERENT POLYGONS around a vertex which has the same arrangement of polygons

Semi-regular tessellation

__________________ is an edge-to-edge tessellation, but the order or arrangement of polygons at each vertex is not the same

Demi-Regular Tessellation

The function which iterates a figure to make it smaller and smaller or bigger and bigger using a scaling factor is called ___________

Fractals

______________ are mathematical constructs characterized by SELF-SIMILARITY. This means that as one examines finer and finer details of the object, the magnified area is seen to be like the original but is not identical to it

Fractals

___________ is basically the same figure being smaller and larger while ___________ is just being categorized as being ALMOST IDENTICAL to the original

Dilation
Fractals

____________________ means REPEATING A PROCESS OVER AND OVER. It means repeating a function over and over

Iteration

The _______________________ (IFS) is a method for generating fractals involving a large number of calculations of a simple formula

Iterative Function System

__________________ is a special kind of iteration. With this, there is a given starting information and a rule for how to use it to get new information.

Recursion