Wisk: Afgeleiden & Integralen

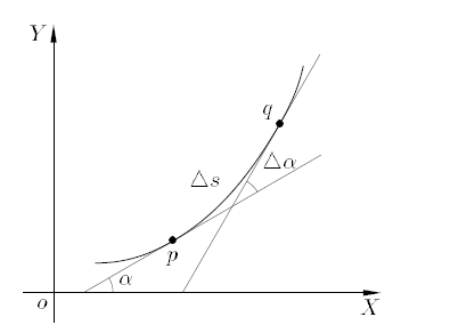
Differentiequotiënt meetkundig

De richtingscoëfficiënt van de rechte lijn (koorde) pq door de punten p(a – f(a)) en q(a+h – f(a+h)) • Formule: [f(a+h) – f(a)]/h

Afgeleide meetkundige betekenis

De richtingscoëfficiënt van de raaklijn aan de kromme y=f(x) in het punt (a – f(a)) (Illustratie aanbevolen)

Horizontale raaklijn

Treedt op als de afgeleide in een punt nul is • f'(a) = 0 • Vaak bij een lokaal extremum (Illustratie aanbevolen)

Verticale raaklijn

Treedt op als de afgeleide in een punt oneindig is • f'(a) = ∞ (Illustratie aanbevolen)

Verband afleidbaarheid en continuïteit

Als een functie f afleidbaar is in een punt a – dan is f ook continu in a • De omgekeerde stelling geldt niet

Sterkere eis: afleidbaarheid of continuïteit?

Afleidbaarheid is een grotere eis dan continuïteit • Een functie kan continu zijn zonder afleidbaar te zijn

Voorbeeld continu maar niet afleidbaar

De functie y = |x| is continu in het punt 0 – maar niet afleidbaar in 0 omdat de linker- en rechterafgeleide verschillen

Stelling van Fermat

Als f afleidbaar is in c en een lokaal extremum (maximum of minimum) bereikt in c – dan is de afgeleide in c gelijk aan nul (f'(c)=0) (Illustratie aanbevolen)

Stelling van Rolle

Voorwaarde: f continu over [a – b] en afleidbaar over ]a – b[ met f(a) = f(b) • Gevolg: er bestaat een c in ]a – b[ waarvoor f'(c) = 0 (Illustratie aanbevolen)

Betekenis Stelling van Rolle

Als een continue en afleidbare functie dezelfde functiewaarde heeft in twee punten – dan moet er minstens één punt tussenin zijn met een horizontale raaklijn

Kettingregel

Afgeleide inverse functie

Afgeleide van constante k

(k)' = 0

Afgeleide van sin(x)

(\sin x)' = \cos x

Afgeleide van tg(x)

(\tg x)' = \frac{1}{\cos^2 x}

Afgeleide van Bgsin(x)

(\text{Bgsin } x)' = \frac{1}{\sqrt{1-x^2}}

Afgeleide van Bgcotg(x)

(\text{Bgcotg } x)' = \frac{-1}{1+x^2}

Afgeleide van e^x

(e^x)' = e^x

Afgeleide van ln(x)

(\ln x)' = \frac{1}{x}

Afgeleide van sh(x)

(\text{sh } x)' = \text{ch } x

Afgeleide van th(x)

(\text{th } x)' = \frac{1}{\text{ch}^2 x}

Afgeleide van x^k

(x^k)' = k x^{k-1} waarbij k ≠ 0

Afgeleide van cos(x)

(\cos x)' = -\sin x

Afgeleide van cotg(x)

(\text{cotg } x)' = \frac{-1}{\sin^2 x}

Afgeleide van Bgcos(x)

(\text{Bgcos } x)' = \frac{-1}{\sqrt{1-x^2}}

Afgeleide van Bgtg(x)

(\text{Bgtg } x)' = \frac{1}{1+x^2}

Afgeleide van a^x

(a^x)' = (\ln a) a^x

Afgeleide van log_a(x)

(\log_a x)' = \frac{1}{(\ln a) x}

Afgeleide van ch(x)

(\text{ch } x)' = \text{sh } x

Afgeleide van coth(x)

(\text{coth } x)' = \frac{-1}{\text{sh}^2 x}

Kromming k in punt p

De limiet van de verhouding van de hoekverandering tot de booglengteverandering • k = \frac{d\alpha}{ds}

Kromming k van een cirkel

Het omgekeerde van de straal R • k = \frac{1}{R}

Kromtestraal R

Het omgekeerde van de absolute waarde van de kromming k • R = \frac{1}{|k|} = \left|\frac{ds}{d\alpha}\right|

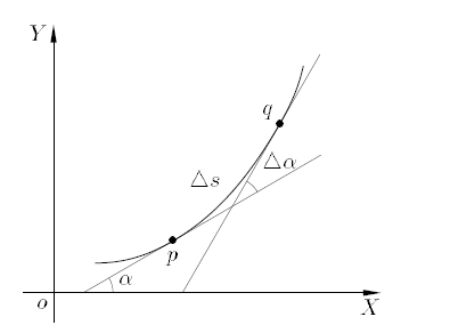
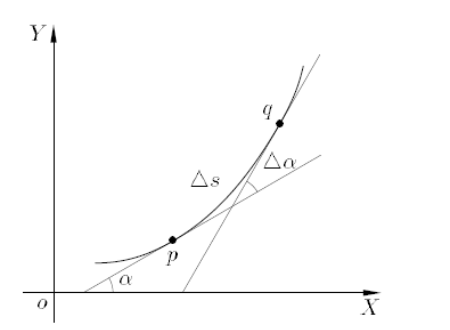
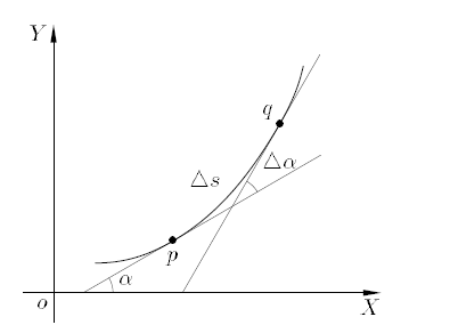
Formule kromming k

k = \frac{y''}{(1 + y'^2)^{3/2}}

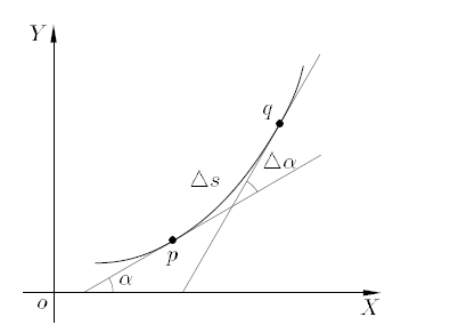
Formule kromtestraal R

R = \frac{(1 + y'^2)^{3/2}}{|y''|}

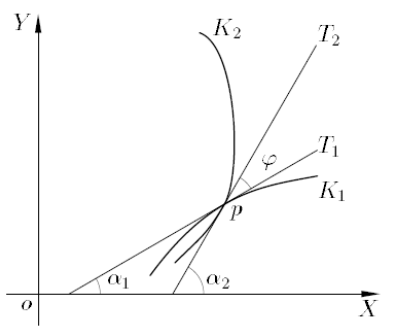
Hoek φ tussen krommen K1 en K2

De hoek tussen de raaklijnen T1 en T2 in een snijpunt p

\tg \varphi = \frac{(y'_2)_p - (y'_1)_p}{1 + (y'_1)_p (y'_2)_p}

Richtingscoëfficiënt raaklijn in p

Gelijk aan de afgeleide y' in het punt p • y'_p

Richtingscoëfficiënt normaal in p

Het negatief omgekeerde van de richtingscoëfficiënt van de raaklijn • \frac{-1}{y'_p}

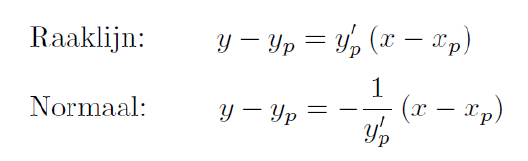
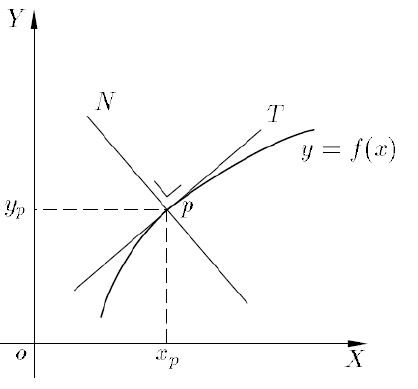
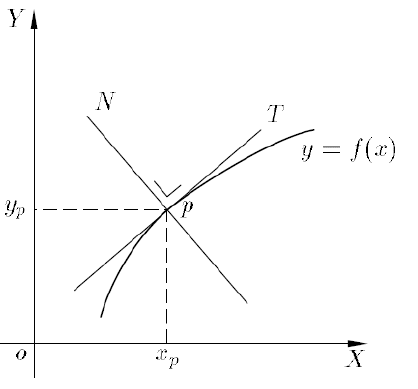
Vergelijking raaklijn in punt p(xp – yp)

y - y_p = y'_p (x - x_p)

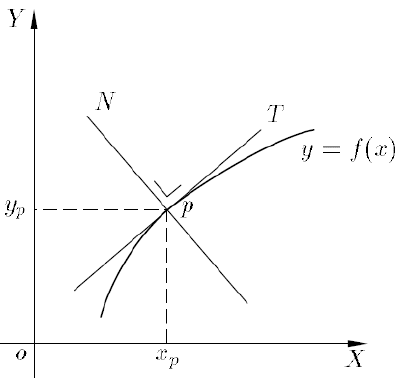
Vergelijking normaal in punt p(xp – yp)

y - y_p = -\frac{1}{y'_p} (x - x_p)

Substitutiemethode bij integreren

1) Vervang een stuk door t

2) bereken dt = d(t) * dx —> dx = …/dt

3) dx invullen

4) bereken vereenv integraal, vul daarna pas de t terug in

Partiële integratie idee

Gebruik partiële integratie wanneer integrand product is van twee functies die je apart goed kent

Partiële integratie formule

Voor afleidbare f en g geldt ∫f(x) g'(x) dx = f(x) g(x) - ∫f'(x) g(x) dx

∫ f g ′ = f g − ∫ f ′ g

Partiële integratie keuze f en g

Kies f zodat afgeleide f' eenvoudiger is • kies g' zodat je g gemakkelijk kan integreren

Partiële integratie stappenplan

1) kies f en g'

2) bereken f' en g

3) pas formule toe

4) bereken overgebleven integraal

Voorbeeld partiële integratie x ln x

Neem f(x) = ln x en g'(x) = x • dan is f'(x) = 1/x en g(x) = x^2/2

Wanneer substitutie gebruiken

Gebruik substitutie als je een duidelijke binnenfunctie ziet waarvan de afgeleide ook in de integraal voorkomt

Wanneer partiële integratie gebruiken

Gebruik partiële integratie bij product van een logaritme • macht • exponentiële functie met eenvoudige afgeleide of primitieve

Stappenplan partiële integratie

1. Herken een product in de integraal (\int f(x)g'(x),dx).

2. Kies (f) als de factor die eenvoudiger wordt na differentiëren.

3. Kies (g') als de factor die je gemakkelijk kan integreren om (g) te vinden.

4. Bereken (f') en (g).

5. Gebruik de formule
   ∫ f g ′ = f g − ∫ f ′ g

6. Los de nieuwe integraal (\int f'(x) g(x),dx) op (meestal eenvoudiger dan de oorspronkelijke).

De integraal van dx

\int dx = x + C als onbepaalde integraal

De integraal van x^n dx

\int x^n dx = \frac{x^{n+1}}{n+1} + C als n ≠ -1

De integraal van e^x dx

\int e^x dx = e^x + C als onbepaalde integraal

De integraal van 1/x dx

\int \frac{1}{x} dx = \ln|x| + C als onbepaalde integraal

De integraal van a^x dx

\int a^x dx = \frac{a^x}{\ln a} + C als a ∈ R^+₀ \ {1}

De integraal van 1/√(a^2 - x^2) dx

\int \frac{1}{\sqrt{a^2 - x^2}} dx = \text{Bgsin} \frac{x}{a} + C als a ≠ 0

De integraal van 1/√(x^2 + b) dx

\int \frac{1}{\sqrt{x^2 + b}} dx = \ln|x + \sqrt{x^2 + b}| + C als b ≠ 0

De integraal van 1/(x^2 + a^2) dx

\int \frac{1}{x^2 + a^2} dx = \frac{1}{a} \text{Bgtg} \frac{x}{a} + C als a ≠ 0

De integraal van 1/(x^2 - a^2) dx

\int \frac{1}{x^2 - a^2} dx = \frac{1}{2a} \ln \left| \frac{x - a}{x + a} \right| + C als a ≠ 0

De integraal van sin x dx

\int \sin x \

De integraal van cos x dx

\int \cos x \

De integraal van 1/cos^2 x dx

\int \frac{1}{\cos^2 x} dx = \text{tg} x + C als onbepaalde integraal

De integraal van 1/sin^2 x dx

\int \frac{1}{\sin^2 x} dx = -\text{cotg} x + C als onbepaalde integraal

De integraal van sh x dx

\int \text{sh} x \

De integraal van ch x dx

\int \text{ch} x \

De integraal van 1/ch^2 x dx

\int \frac{1}{\text{ch}^2 x} dx = \text{th} x + C als onbepaalde integraal

De integraal van 1/sh^2 x dx

\int \frac{1}{\text{sh}^2 x} dx = -\text{coth} x + C als onbepaalde integraal

Wat is de integraal voor de OPPERVLAKTE VAN EEN VLAK GEBIED

(POOLKROMMEN)

S=\frac{1}{2}\int_{\theta1}^{\theta_2}r^2{}d(\theta)

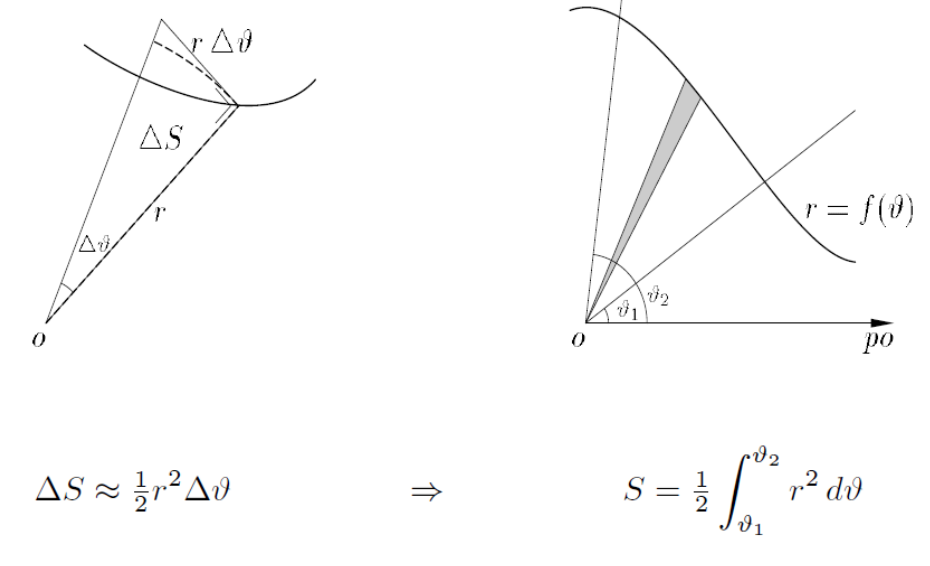
Wat is de integraal voor de OPPERVLAKTE VAN EEN VLAK GEBIED

(PARAMETERKROMMEN)

OPPERVLAKTE VAN EEN meervoudig VLAK GEBIED

(POOLKROMMEN)

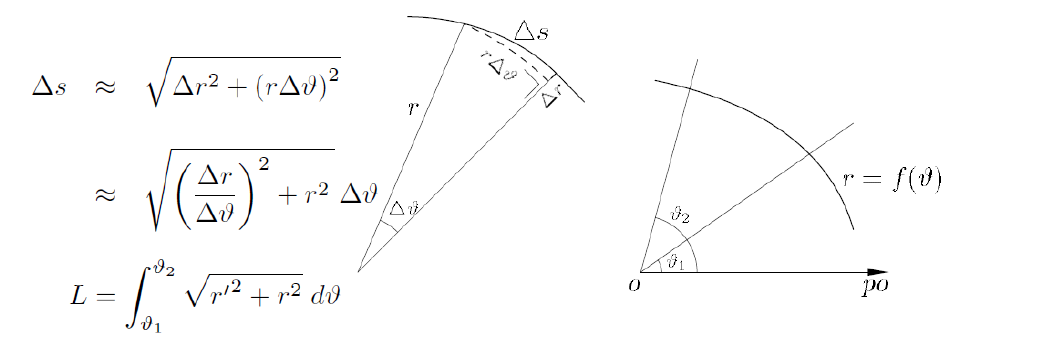
wat is de integraal voor de BOOGLENGTE VAN EEN VLAKKE KROMME (cartesisch)

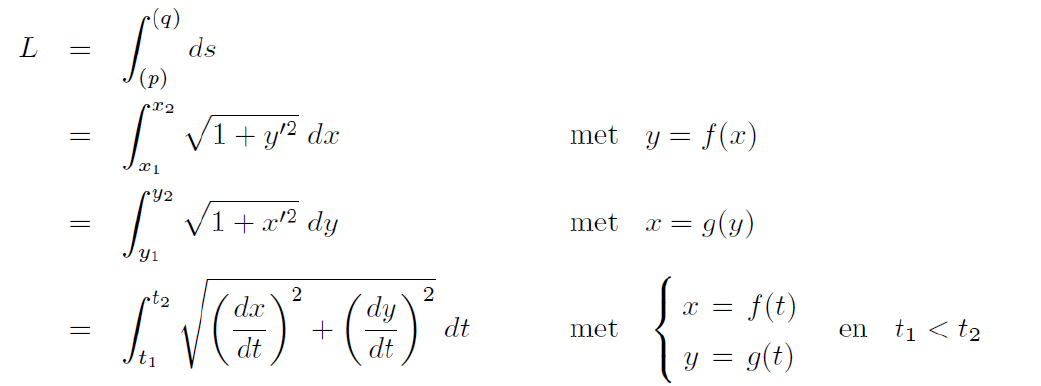
wat is de integraal voor de BOOGLENGTE VAN EEN VLAKKE KROMME (poolcoordinaten)

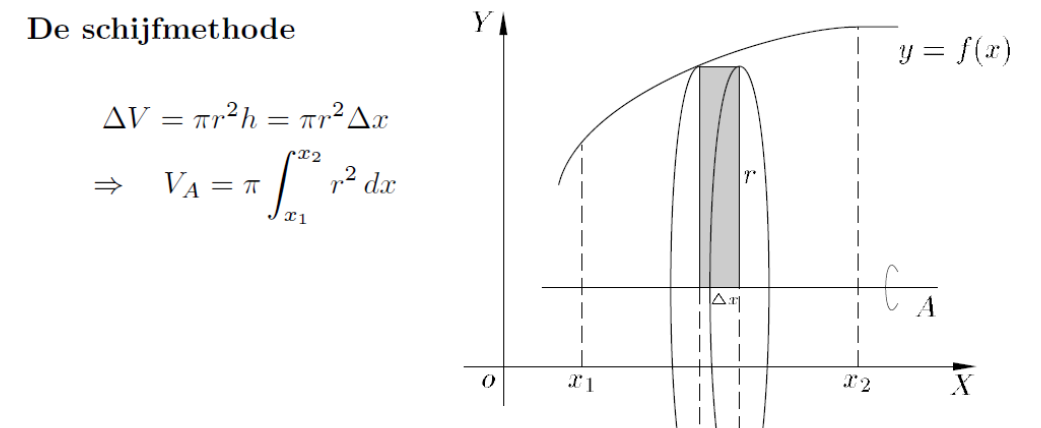
wat is de integraal voor een VOLUME VAN EEN OMWENTELINGSFIGUUR (schijfmethode)

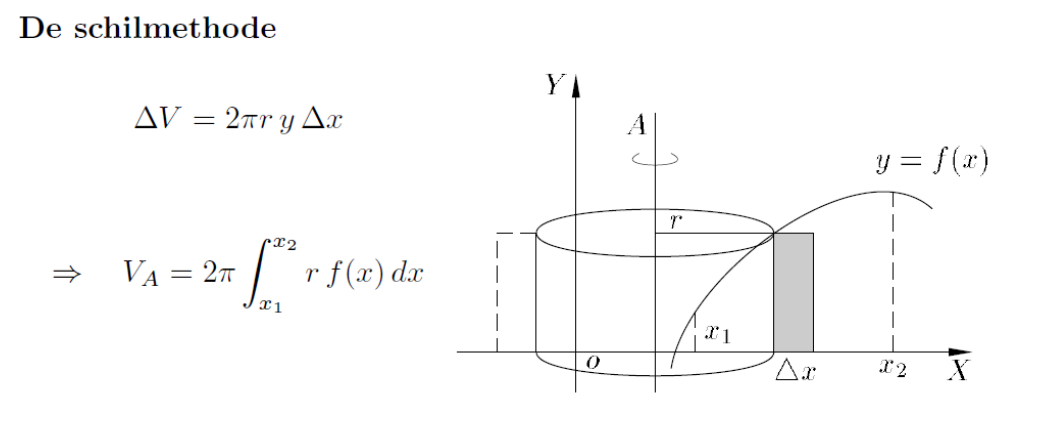
wat is de integraal voor een VOLUME VAN EEN OMWENTELINGSFIGUUR (schilmethode)

wat zijn de integraln voor de ZIJDELINGSE OPPERVLAKTE VAN EEN

OMWENTELINGSFIGUUR

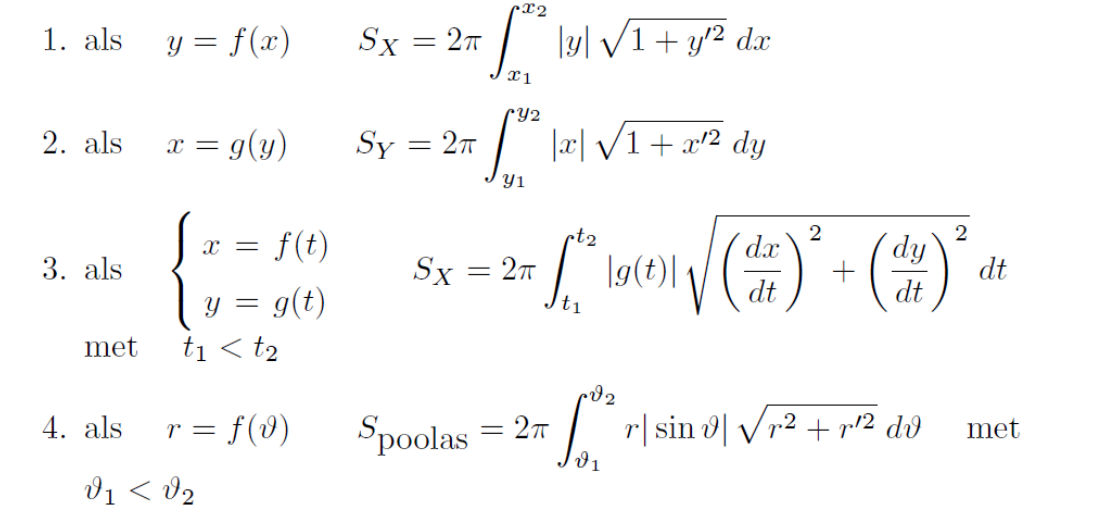
Wat zijn de integralen voor TRAAGHEIDSMOMENT / STATISCH MOMENT

Wat is de integraal voor het ZWAARTEPUNT VAN EEN HOMOGENE BOOG

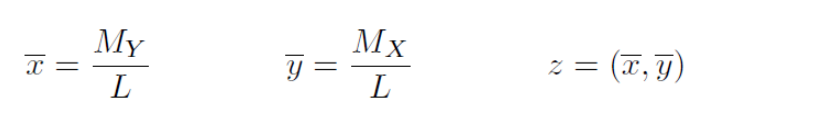
Stelling 1 van Guldin

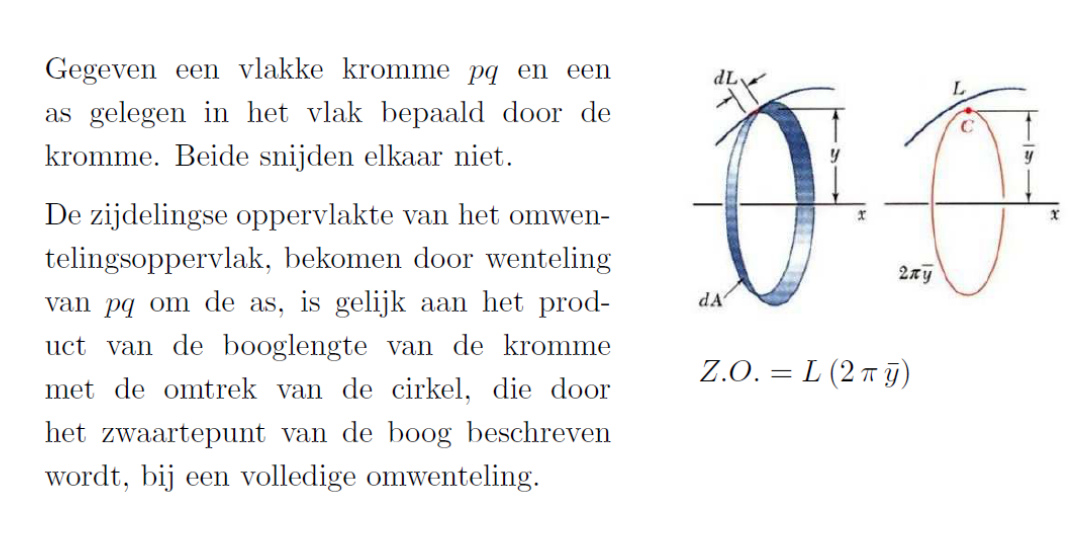
Stelling 2 van Guldin