X-rays

Describe the basic principle of an X-ray tube (3 steps)

• Electrons are emitted via. cathode

• Accelerated by an electric field to an anode

• Collides with a target

Notes:

• when e- hits the anode, it decelerates and emits x-rays

• change in velocity due to energies x10keV (low)

What 3 things do the electron collisions in an x-ray tube give rise to?

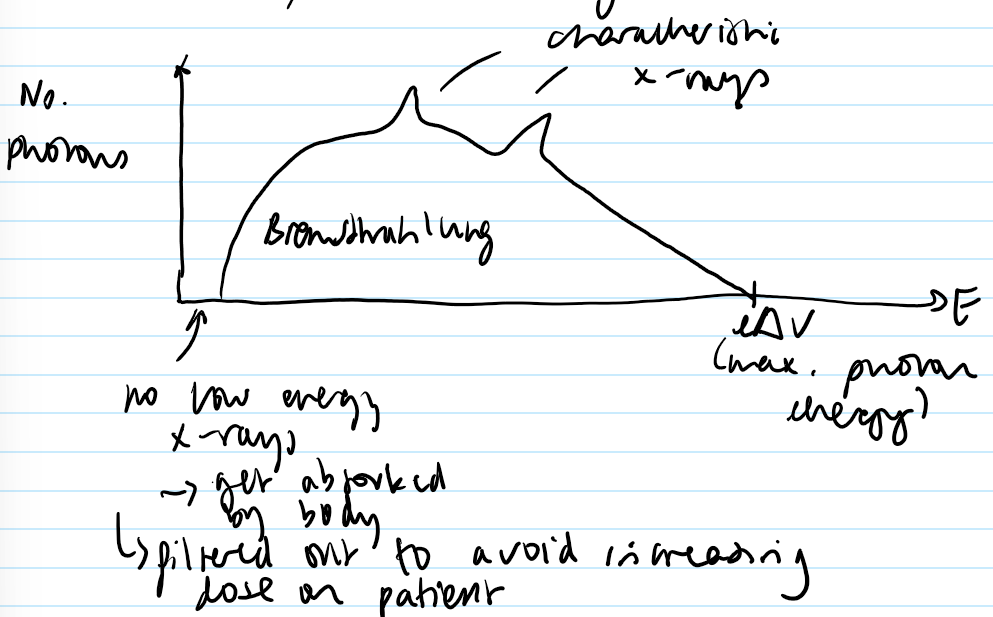
1) Bremsstrahlung x-rays

2) Characteristic x-rays

3) Heat

max. energy gained by an electron = e delta v

State and explain the 2 main processes after an electron interacts with a target

1) Bremsstralung x-rays: ENERGY LOST in the form of this x-ray

• German: “Breaking radiation“

• consider particle charge e, scattered by a nucleus of charge Ze

• a Coulomb force: F directly proportional to Ze²

• Resulting acceleration direc. prop. to Ze²/m

• Deceleration causes emission of EM radiation, where:

• power of radiation direc. prop. to a²

• power direc. prop. to z²e⁴/m²

• produces a continuous x-ray spectrum

From an x-ray tube, higher power is required:

• decrease mass m

• increase Z of target

• max. energy of emitted photon:

  • occurs when electron loses all its kinetic energy

  • hv_max = e delta v

  • v_max = max. frequency of x-rays

2) Characteristic x-rays: specific to different energies

• caused by collisions with atomic electrons

• incident electron excites or ionizes an atom

• electronic energy level is filled by downward transitions

• causes emissions of x-rays of identical frequencies

  • characteristic wavelengths shown

• compute energy of characteristic x-rays using the Bohr model of the atom:

  • Energy levels in an atom according to the Bohr model:

    • En = (1/n²)*(-m_e*q_e^4 (Z-1)² / (8*h²*eps_0²))

    • n = principle quantum number

    • can derive an approximate formula for energy difference when electrons transition between shells:

      • see image

Draw the x-ray spectrum for an x-ray tube. Label the axes, along with the Bremsstrahlung and characteristic x-rays. Note anything else that may be important.

• can change the energy spectrum by changing the target material to shift k_alpha and k_beta lines

• e.g. molybdenum:

  • k_alpha = 17.9 keV

  • k_beta = 21 keV

• lower energies give better soft tissue contrast

State the ranges for hard and soft x-ray energies- explain their uses.

Hard: E> 10keV

• penetrate liquids, some solids

• used for diagnostic imaging

Soft x-rays: E< 10keV

• hardly penetrate matter

Explain the basic idea of a planar x-ray.

Assuming an isoenergetic beam, derive an equation for the beam intensity with distance.

mu is the attenuation coefficient.

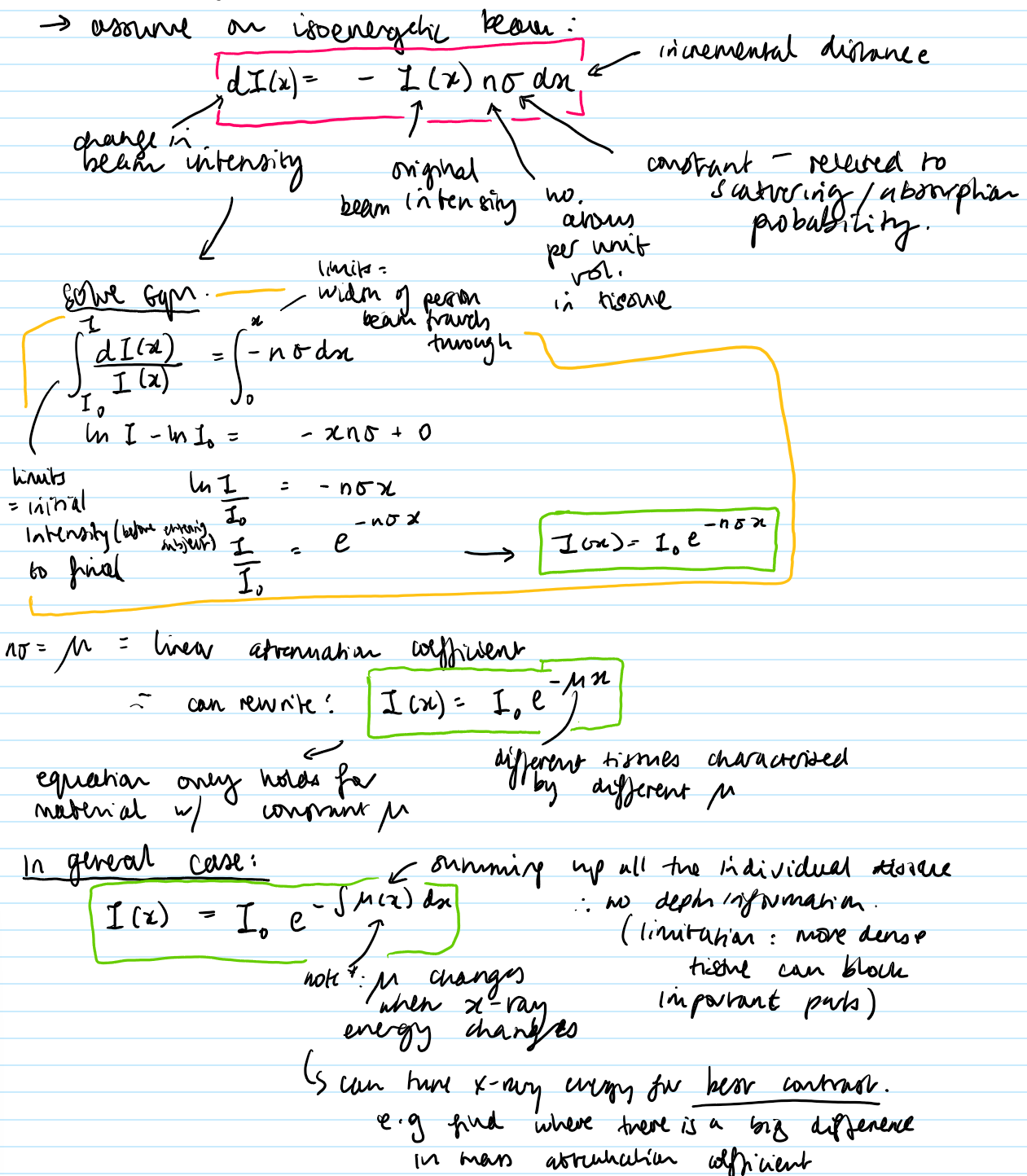
State and explain the 3 mechanisms of interaction of x-rays with matter.

1) Photoelectric effect

• photon interacts with an electron

  • electron is emitted from the atom and photon absorbed

  • contribution of photoelectric effect to mu:

  • mu_PE ~ ez³/E³

  • most important at low energy & for tissues with high z values

2) Compton scattering

• photon scatters by a weakly bound electron

  • electron is ejected from the atom

  • photon energy is released by an amount, depending on the scattering angle

  • contribution of scattering to mu:

  • mu_CS direc. prop. to p (approx.)

3) Pair production

• photon interacts with a nucleus, forming electron/position pair

• only happens for photon energy > 1.02 MeV

  • (rest mass of electron and position)

• less relevant for diagnostic x-rays

Draw a graph of mu against the energy of a photon for each mechanism of interaction, labelling the diagram. Explain which is most important.

What are Fourier Transforms useful for?

• a way to assess frequency content of a signal or optical frequencies in an image

• they consider phase

What do the low and high frequencies in a spatial domain correspond to?

Low:

• represent overall spatial structure

High:

• represent smaller, rapidly-changing features

State the 1D FT and 1D FT equations for functions F(k) and f(x)

State the 2D FT and 2D IFT equations for F(k_x, k_y) and f(x, y)

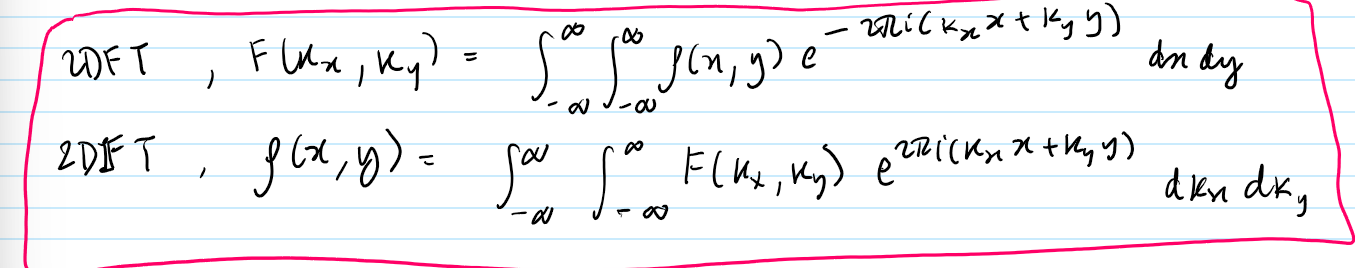
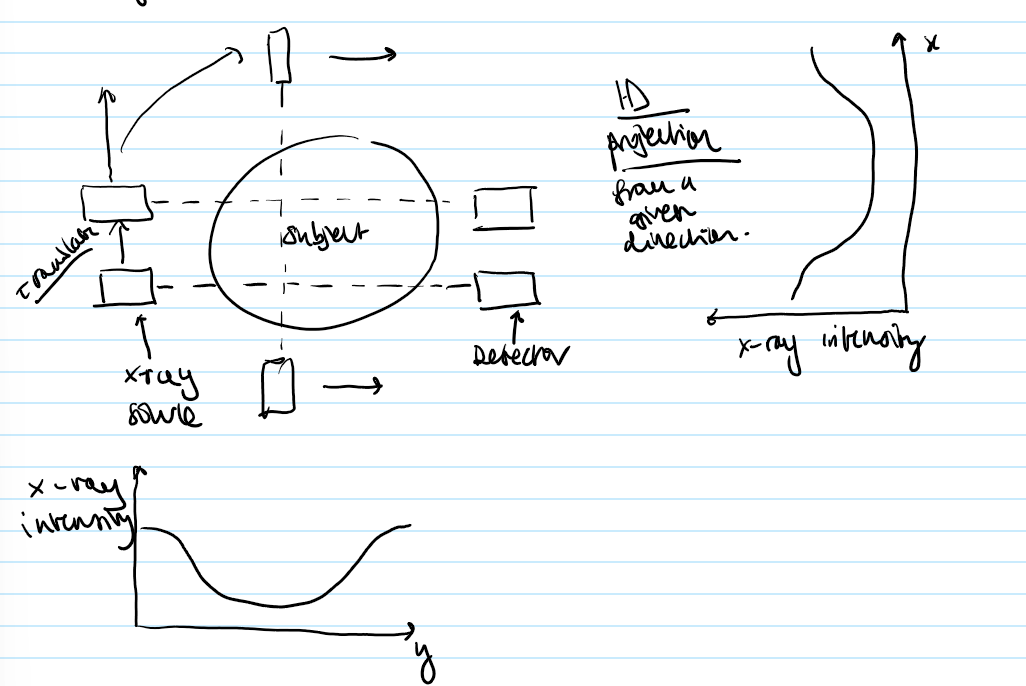
Describe the principles of Translate-rotate x-ray CT + draw a plot of x-ray intensity vs. distance from the beam in the y direction.

1) A series of pencil- narrow beam x-rays- beam shines through the subject (defined by lead collimators)

2) Source + detector: translated across the body

3) Attenuation of the beams allows definition of a projection from a given direction

What is the intensity (as a function of distance r) given by, hence the projection? Draw a diagram of the rays going through a subject, with labels to help.

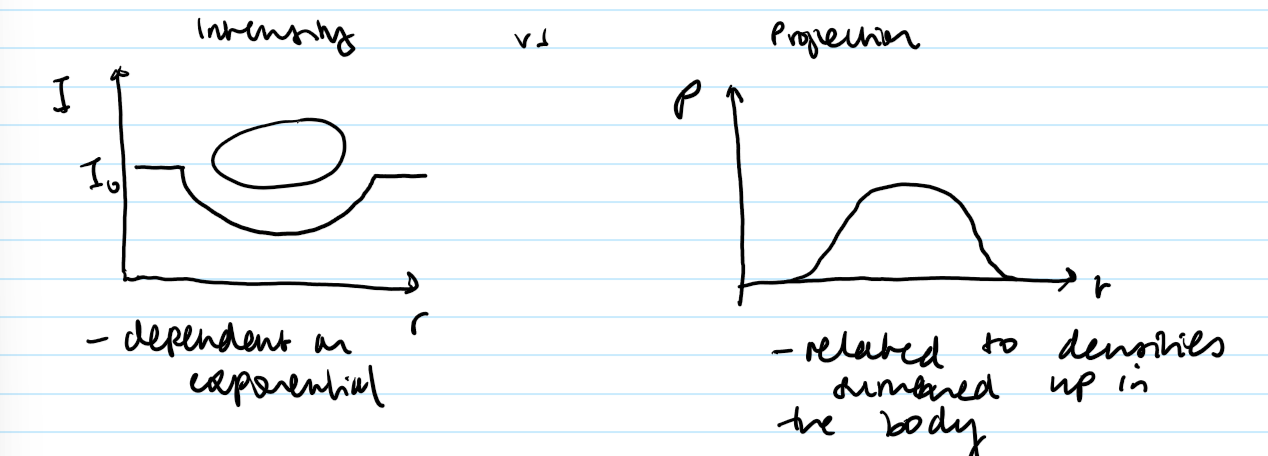
Draw two plots: intensity and projection against r as rays pass through a subject.

State what they are dependent on.

• projections are spread across object

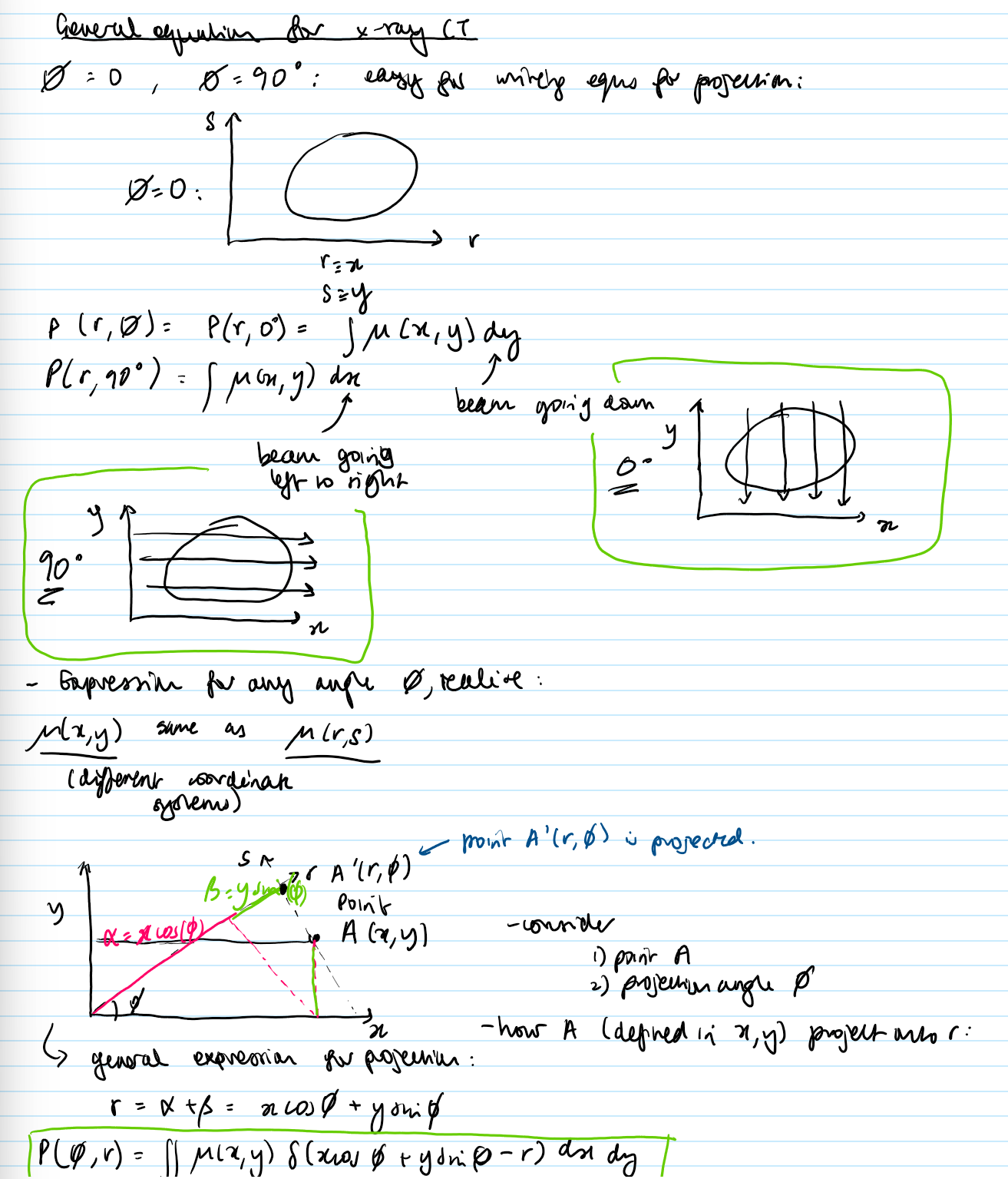
What is the general equation for projection?

• everything is - apart from path xcos phi + ysin phi

• this picks out a path

• want the attenuation- image of the slice

  

What type of process is used to invert the equation and reconstruct mu(x, y) from P(phi, r)?

Back projection construction

What does Central Section Theorem state? What does it prove?

States: “1D FT of a projection through an object is the same as a section through the 2D FT of the object itself along the Fourier conjugate of the projection.”

1DFT (P(phi, r) —> 2DFT (mu(x, y))

Proves there is enough information in the projections to define M(k_x, k_y) and so mu(x, y)

Starting from an axial slice and defining the 1DFT of the projection of that slice, prove the Central Section Theorem.

What is the disadvantage to the Central Section Theorem?

• it’s non-uniform sampling of k-space

• need different method of reconstruction

What is the basic principle of Crude Back Projection reconstruction?

• generated by spreading each projection back across image space and adding them together

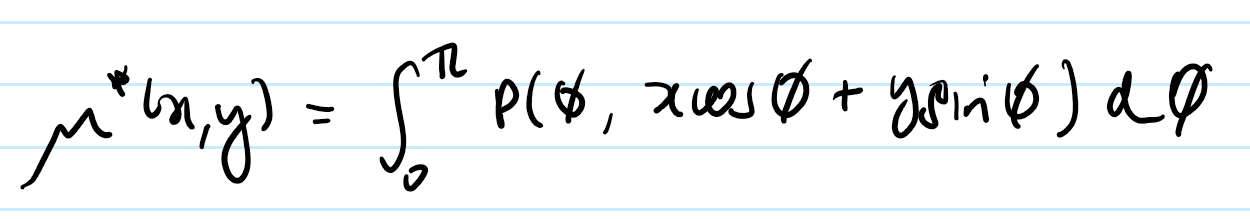
Crude back projection…
Use the expression to relate reconstructed image mu* to real image mu(x,y)

M*(k_x, k_y) = M(k_x,k_y)/k_r
M = 2DFT of the object
M* = 2DFT of the image

- spatial frequencies down weighted in proportion to their magnitude

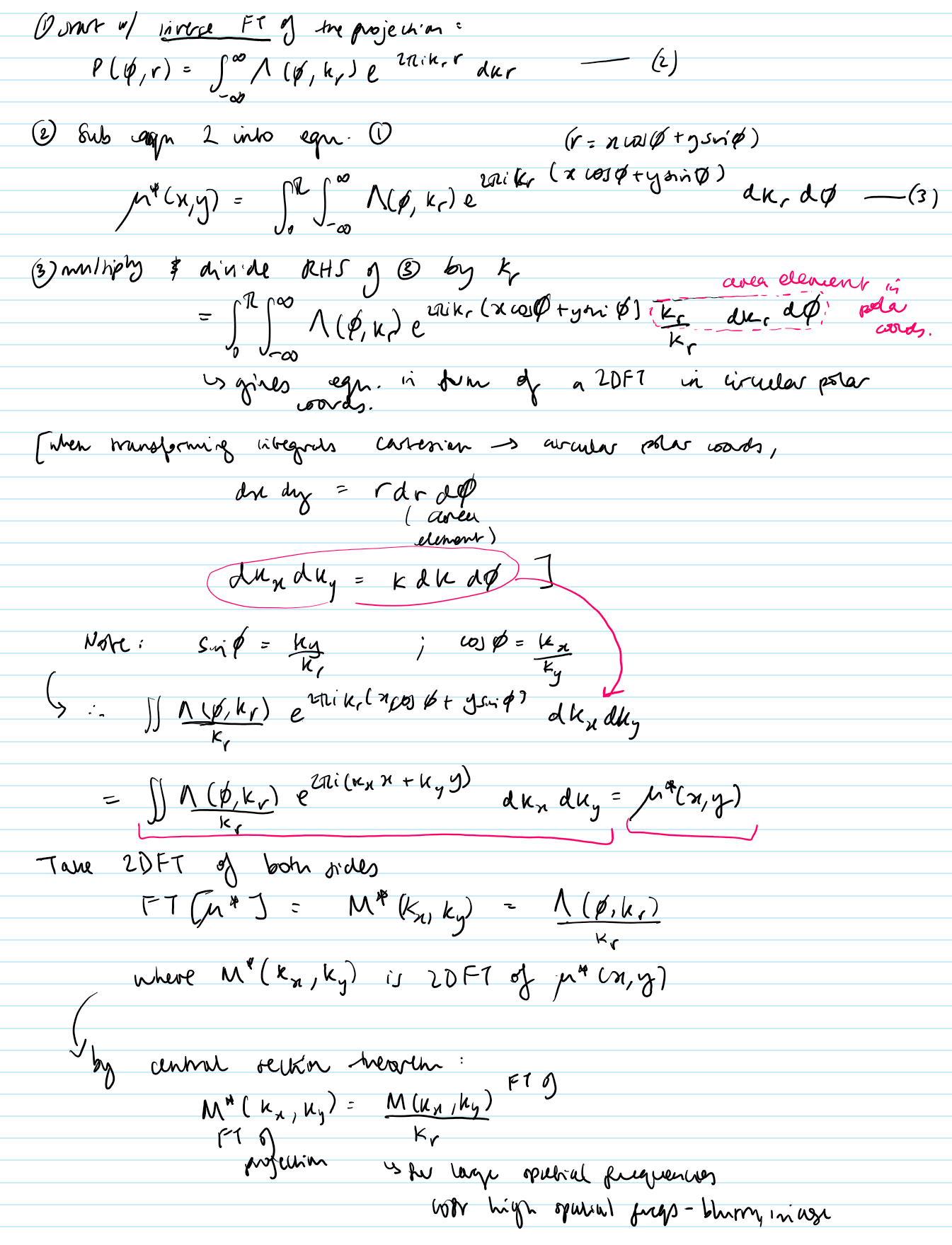
What are the basic principles of Filtered Back Projection? (3 things)

• corrects blurring

• projects P’, a filtered version of each projection

• amplifies components in projection in proportion to their spatial frequency

Give a disadvantage for Filtered Back Projection

• can also amplify high-frequency noise which is unwanted!

Give the basic principles of Iterative Back Projection.

• an alternative to FBPR

• numerical technique

• results in better images

Based on algorithm:

1) Make a guess at the object by making PxQ grid of numbers

2) Use guess to make simulated projection

3) Compare simulated projections to the real projections and update the guess

Note:

• also becoming more popular

Path length: simulated projections…
How to find the real object from the iterative BPR?

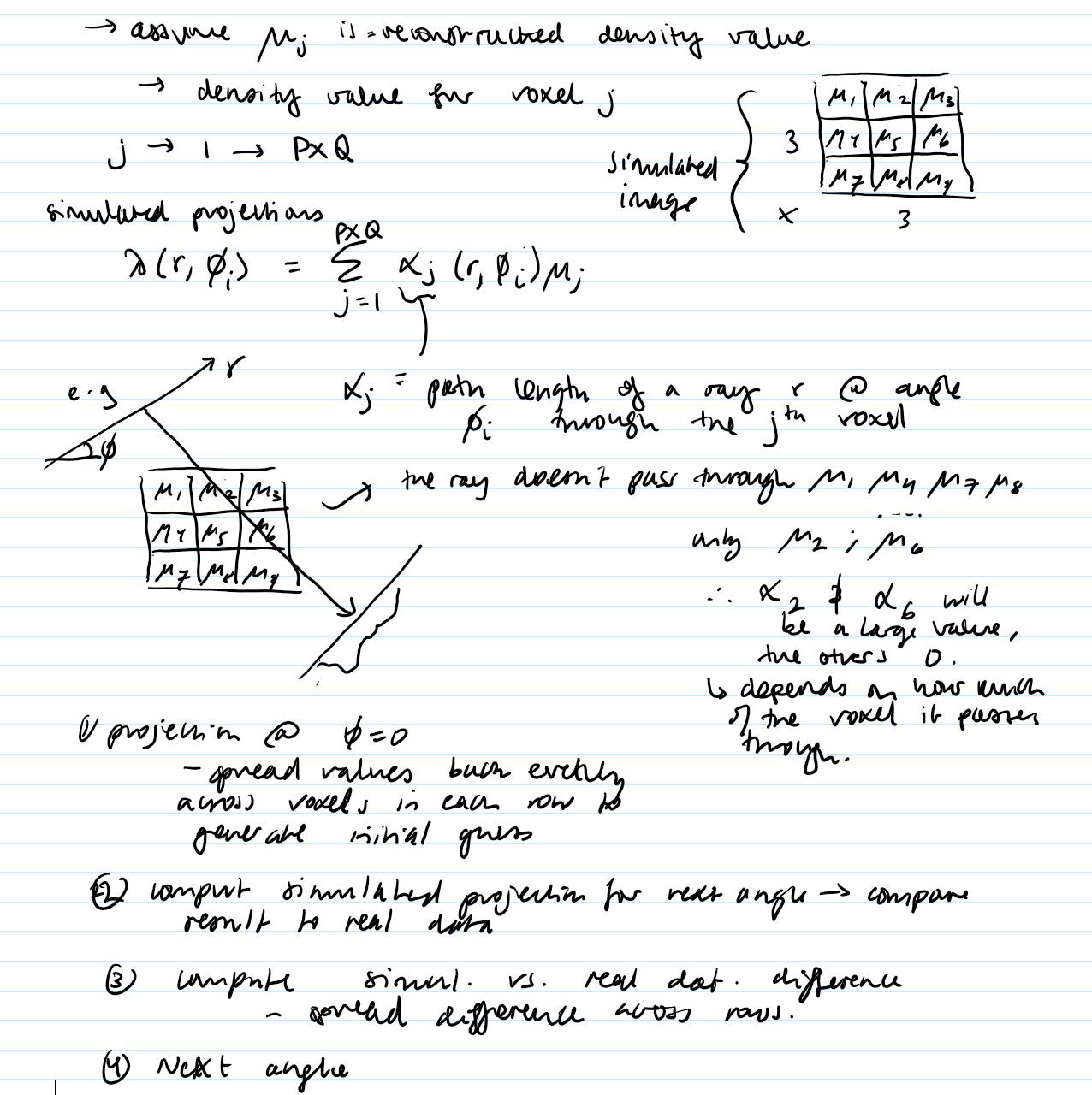
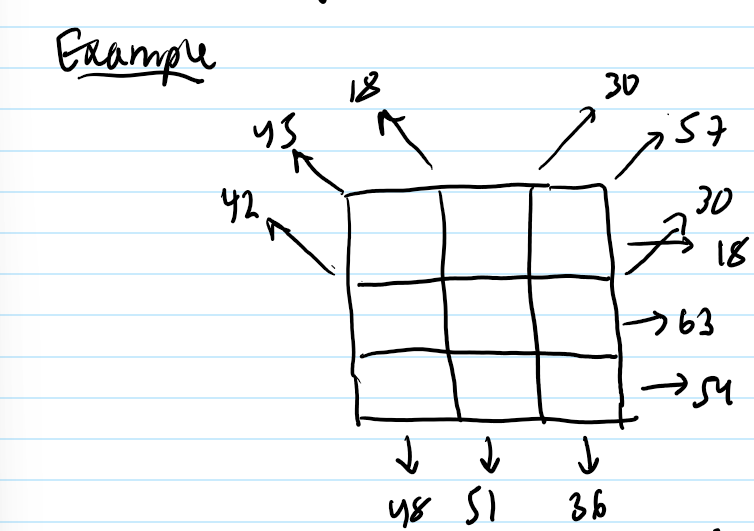
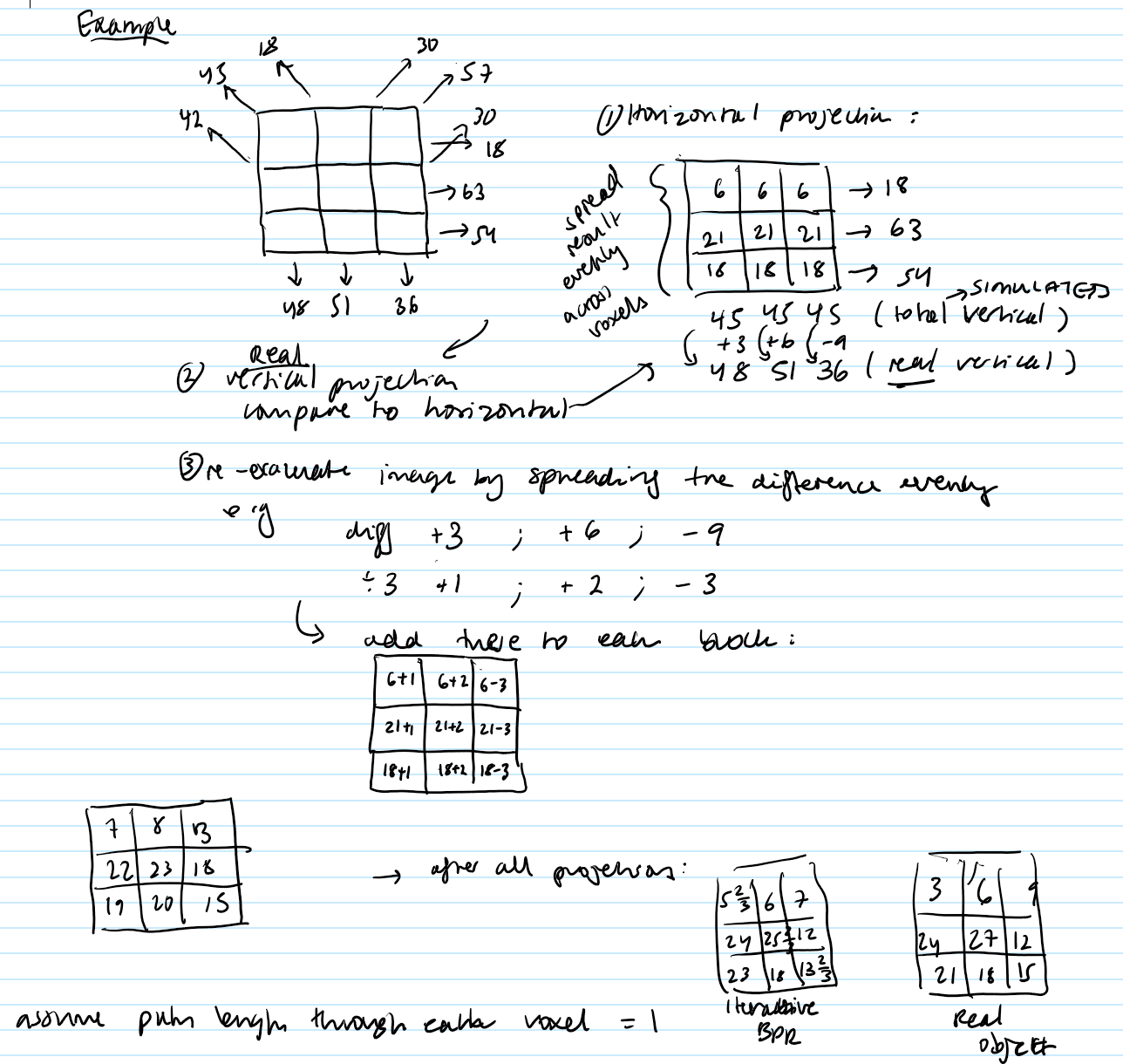
Using various projections calculate the possible real projection from the grid. Assume the path length through each voxel = 1.

What is the main source of noise in x-ray CT?

• photon noise

How is the signal-to-noise ratio (SNR) calculated from the number of photons?

SNR = sqrt(N)
high photons = good SNR
but wanna avoid it!!

What can generate higher SNR? What are the disadvantages to this?

• increasing voxel size

• leads to partial voluming

What is beam hardening and what can it lead to?

• X-ray has multiple energies, so the average beam energy is higher as the beam travels through the tissue

• this can lead to artefacts (unreal images)