Lecture 20-21 - Elastic Potential Energy Potential Energy and Conservation of Energy

elastic potential energy

The______________ of an object-spring system is the energy stored in the spring when it is either compressed or stretched from its natural length. The work done by the spring relates to the force it exerts as it returns to its equilibrium position.

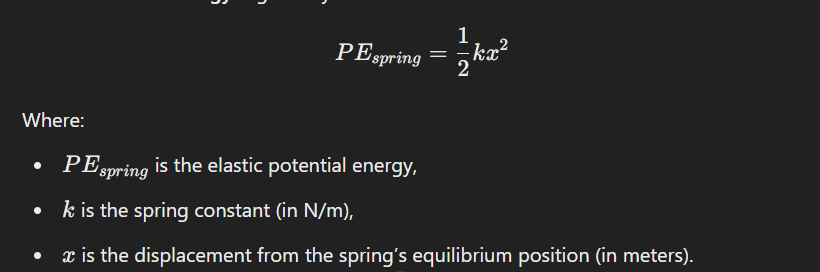
work done by the spring

The __________ is the energy transferred as the spring moves an object back toward equilibrium.

PE_spring = -1 (½ kx² - ½ kx²)

When the spring is compressed or stretched, the force exerted by the spring does work to restore the system to its original position, and this work equals the change in the spring’s potential energy. What represents this?

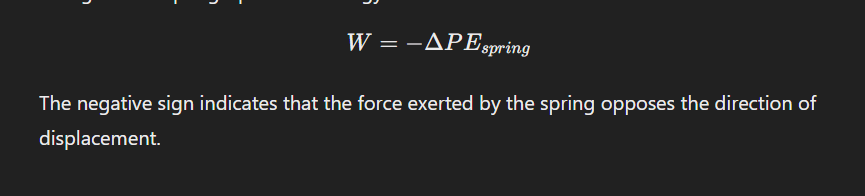
E_total= KE + PE_spring = constant

As the object moves, energy is exchanged between kinetic energy and potential energy:

• When the object is at maximum displacement (either compressed or stretched), its velocity is zero, so all the energy is stored as potential energy.

• When the object passes through the equilibrium position (natural length of the spring), all the potential energy has been converted to kinetic energy, and the velocity is at its maximum.

Conservative forces (e.g., spring forces, gravitational forces)

Qualitative Expression: Conservation of mechanical energy states that in a closed system with only ___________, the total mechanical energy remains constant.

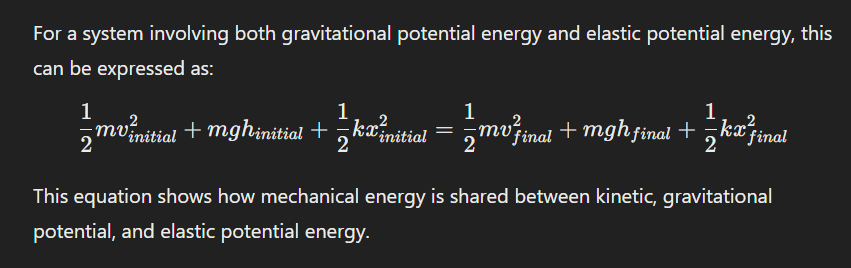
Hooke’s Law

_______________. It states that the force required to extend or compress a spring by some distance is proportional to that distance.

Spring Constant

The ___________ is unique to each spring and determines how stiff or flexible the spring is. A larger k means the spring is stiffer and requires more force to stretch or compress it by a given amount.

restoring force

The force described by Hooke’s Law is a ____________ it acts to bring the spring back to its equilibrium position, whether it’s stretched or compressed.

Dividing the force by the displacement to get N/m for spring constant.

If you pull on a spring with a force of 10 N and the spring stretches by 0.2 meters, the spring constant k can be calculated using Hooke’s Law:

Force depends on the displacement x.

The spring constant is a non-constant force. Which means that the ________.

W = ½ k(x₂)²- ½ k(x₁)²

Consider a spring stretched from a distance x1 to x2. The work done on the spring is ___________.

W_^el = ½ k(x₁)² - ½ k(x₂)²

Consider a spring stretched from a distance x1 to x2. The work done by the spring according to Newton’s 3rd law is ___________.

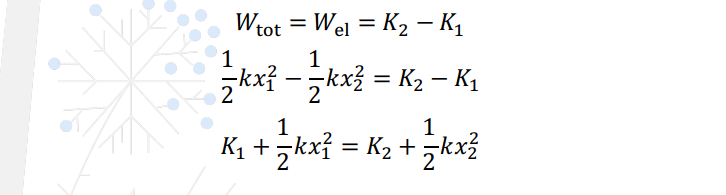
W_^el: K₂ - K₁ = ½ k(x₁)² - ½ k(x₂)²

If the only force that does work on a system is the force of a spring, then from the work-energy theorem, we can write __________. Where the force of the spring can be defined as the elastic potential energy.

U_^el: ½ k(x₁)² or the Elastic potential energy

____________ is the energy stored in an object when it is stretched or compressed within its elastic limit. This typically occurs in systems like springs, rubber bands, or any material that can return to its original shape after being deformed. The energy is stored as potential energy and can be released when the object returns to its equilibrium position.

Dependence on Displacement

Elastic potential energy has a ________. The amount of energy stored is proportional to the square of the displacement x. This means that doubling the displacement quadruples the energy stored.

spring constant 𝑘

The ____________ determines how much energy is stored for a given displacement. A stiffer spring (higher 𝑘) stores more energy for the same displacement.

K₁+ U_total,1 + W_others = K₂ + U_total, If W_others = 0, energy in the system is conserved.

Conservation of Mechanical Energy Equation.

Check for initial and final states, choose y=0, identify forces involved (gravity, spring, friction), is the object moving or at rest.

Conservation of Mechanical Energy Problem Solving Tips.

Potential energy decreases as y decreases.

Gravitational Potential Energy - Position (y) graph relation.

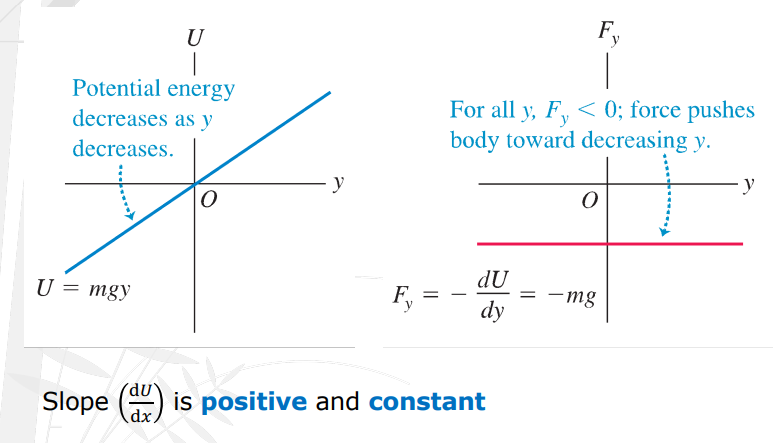
If slope is negative and decreasing, and if positive, increasing elastic potential energy.

Elastic Potential Energy - Position (x) graph relation.

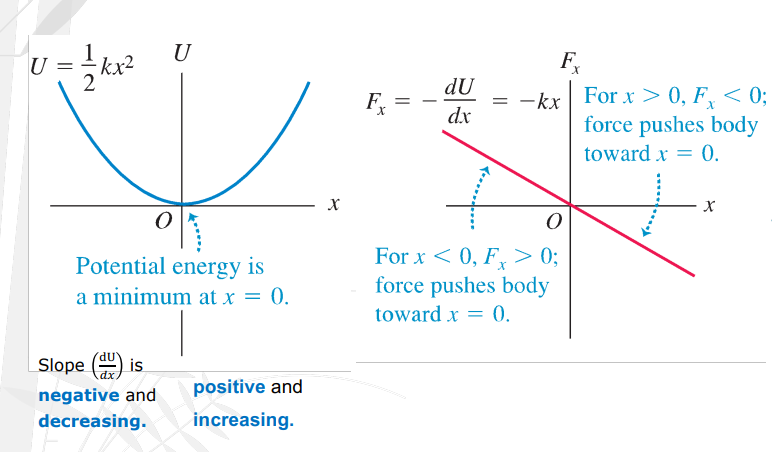
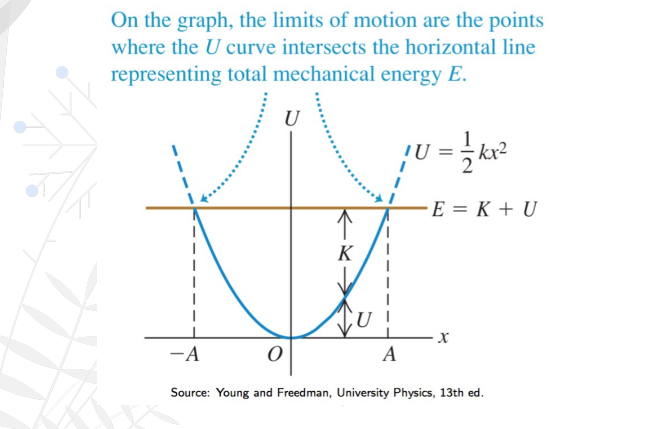
potential energy function U(x) and the total energy

Features of the Energy Diagram: Energy diagrams are graphs that show both the _____________ of the particle subjected to the force that corresponds to U(x),

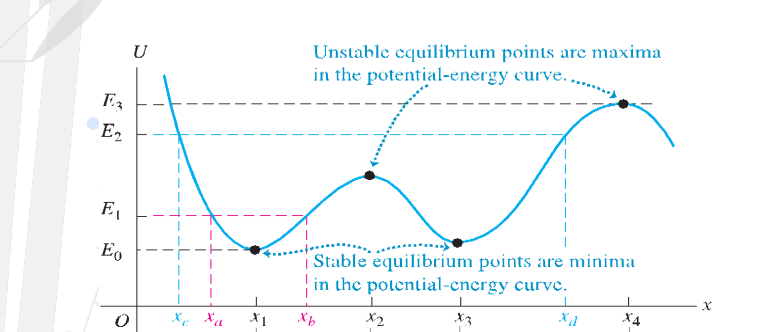
Stable , Unstable, Neutral Equilibrium

Equilibrium condition: F=0 happens in three ways wherein ________

Stable Equilibrium

__________ points are minima in the potential-energy curve. Object tends to return to its original position.

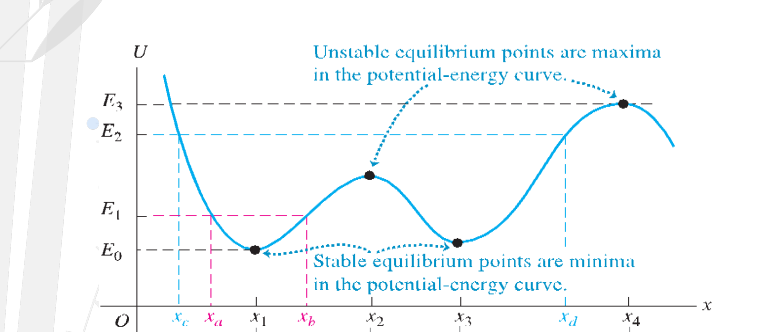
Unstable Equilibrium

__________ points are maxima in the potential-energy curve. Displacement tends to increase.

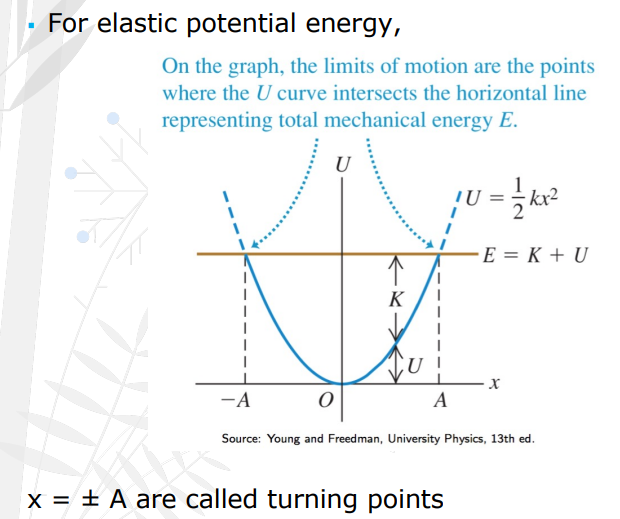
x = ± A are called turning points

Both these __________ all energy is stored as potential energy and the velocity (hence K) is zero. As the system moves, energy oscillates between kinetic energy (K) and potential energy (U).

Kinetic Energy

At the equilibrium point x=0, all energy is ___________ and the potential energy is zero.