Physics Unit C - Waves

cycle

one complete oscillation of a pendulum also used to describe circular motion in 2pi

equilibrium position

is the position where the pendulum bob would rest if not disturbed

amplitude

max displacement from equilibrium position

time period

time take for one cycle

time period is dependent on length of string

W² = g/L

W = 2 pi f

T = 2 pi Squareroot of (L/g)

frequency

number of cycles that pendulum makes per unit time. this is equal to 1/time period

angular frequency

found by multiplying F by 2pi (w=2pif). This quantity is normally used when describing circular motion. an angular frequency of 2pi rad s^-1 means that a body makes one revolution per second or one complete cycle or oscillation

Simple Harmonic Motion

motion that takes place when acceleration is directed towards equilibrium and proportional to amplitude

• bigger amplitude larger acceleration

acceleration

is proportional to direction

• the displacement has to be in opposite direction of acceleration

gravity = changing acceleration

what are the constants of proportionality (w² )

y = acceleration

x = displacement

m = constant of proportionality

has to go through origin

what are the approximations for SHM

• displacement is horizontal, slightly up

• force acting towards equilibrium position is horizontal component of tension F_t sintheta, the resultant force of the tension and weight

• weight about same as tension F_t = mg restoring force F_t sintheta = mgsintheta

restoring force

sintheta = x/L

F = (mgx)/L

ma = (-mgx)/ L

mass on a spring

if more spring is pulled down the force in the spring increases

same conditions, also SHM:

• force towards equilibrium

• acceleration proportional to amplitude

if displacement is down (-) then acceleration is up and positive

at equilibrium, ma = -kx

a = -kx/m

T = 2pi squareroot of m/k

displacement time graph

x = x₀ cos(wt)

displacement negative, acceleration positive

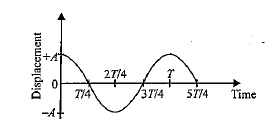
velocity time graph

v = -wx₀ sin(wt)

max velocity = equilibrium

• zero acceleration

min velocity = amplitude

velocity at any given point:

v = w squareroot of (x₀² -x² )

acceleration time graph

if a body is passing through he centre with positive direction":

a = -w² x₀ cos(wt)

max acceleration = amplitude

min acceleration - equilibrium, max velocity

acceleration at any given displacement

a = -w² x

SINE AND COS VARY BY +1 AND -1

kinetic energy

max Ek at the equilibrium moving fastest with max velocity

potential energy

max potential energy at amplitude least amount of velocity

energy at equilibrium

max Ek and it is an undisturbed position thus requires energy to be disturbed

total energy

½ m w² x₀ ² + 0 = ½ mx² x₀ ²

no work done on system, according to law of conservation of energy since total work done is constant

kinetic energy

v =w squareroot of (x₀² -x² )

Ek = ½ mv²

Ek = ½ mw² (x₀² -x² )

kinetic energy at max is at the bottom this x = 0

Ek = ½ mw² x₀²

potential zero

potential energy

Ep = ½ mw² x₀² - ½ mw² (x₀² -x² )

Ep = ½ mw² x²

phase difference of pi from Ek

equation for the displacement of a body that is phase difference apart

in relation to the first body:

x_b =x₀ sin(wt - u)

u = phase difference

what are properties of waves

• echo

• reflect

• continuous

• peak and trophe

pulses

pulses are not waves, they are not reflected, only peak or trophe

two different types of pulses, free and fixed end

When a wave encounters a fixed end, for instance, it comes back upside down. When a wave encounters a free end, it comes back the same way it went out.

superposition

when two pulses meet

constructive interference, where they are in phase with each other creating a wave double in amplitude

destructive interference, the waves are out of phase with each other, result no wave left

continuous wave

if the end of a string is moved up and down with SHM of frequency f, a series of pulses move along the string in a sine curve

transverse wave

the energy given is perpendicular to where the particles go

how to measure a wave

from peak to peak

trophe to trophe

from equilibrium,

longitudinal wave

the vibrations of the particles are along the same direction as the direction of travel

particles left and right pulled back or collided with other particles making it more right than pulled back left

area of compression = peak, particles closer together

areas between compression = trophe = refraction

• seem to get a little further a part

• particles move further form each other

examples of transverse waves

radio waves

light waves

water waves

Seismic S waves

examples of longitudinal waves

sound waves

shock waves

Seismic P wave

sound waves

require particles to move in order to transfer energy

• we know waves can reflect as we hear it echo

environment of sound waves

• when sound passes through warm into cold it refracts. This is why sound carries well in night

refraction

the bending of waves as it passes from one material to another. It bends due to the change in wave speed as it enters a different material.

frequency never changes thus wavelength must be shorter

what properties do light waves all have

• frequency

• amplitude

• wave length

• all move at speed of light

• they do not require a medium to travel through

• they are all transverse waves

• they all transfer energy

• they can all be reflected or refracted

what is light also

it is radiation, all waves on electromagnetic spectrum gave been emitted or radiated by something

damages of exposure to em radiation

excessive exposure can cause damage to living tissue, it depends on frequency of radiation

risks of microwaves

can causing heating of body cells leading to burns

risks of uv

damages the skin and the eyes, leads to skin cancer and eye problems

risks x rays and gamma rays

an cause mutations and or damage cells throughout the body

intensity

it is a measure of the brightness of light in wm^-2 proportional to the square of the wave amplitude

light spreads out so the power per unit area is reduced as we of away from the source

the energy twice as far from the source is spread out 4x the area hence ¼ of intensity

intensity is proportional to amp²

and frequency²

mechanical vs EMF wave

EMF doens’t require a medium mechanical waves do

wavefront

any line that joins points that are in phase with each other

ray

direction of energy transfer

wavefronts and rays are always perpendicular to each other

huygens prinsiple

when wavelengths hits barrier, teh barrier now behaves as a series of wavelets sources sending them in opposite directions

wavelets add to give reflected wavefront

angle of refraction

the angle the light comes out of the second border, always to the normal

if the angle is smaller than the angle incident, ray is slowing down

towarda teh normal is slower and away is faster

angle of incident

the angle the light hits hitting the first border, always to the normal

diffraction of water waves

diffraction is the spreading of waves as they pass through or around an obstacle.

takes place when a wave passes through a small opening, if opening is tiny then wave behaves just like a point source. The wave will seem to pass aorund the small object.

d (opening) = wavelength = diffraction

d> wavelength = no diffraction

d < wavelength = loads of diffraction

interference patterns

the overall distrubance at any point and at any time where the waves meet is the vector sum of the disturbances that would have been produced bue each individual wave

two waves in phase will have constructive interference and create one wave double in amplitude

• always at 0,1,etc the antinodal points with greatest energy

• nλor 2nλ

two waves out of phase with each other will have deconstruction interference and will cancel out

• always at 0.5, 1.5, etc the nodal points where there is no energy

• (2n+1) pi

n = a whole number

a light ray hitting glass

if an incident ray enters glass at an angle it is refracted and bends towards the normal, slowing down

when the ray leaves the glass the opposite happens and it is bent away from the normal, speeding up

frequency is constant

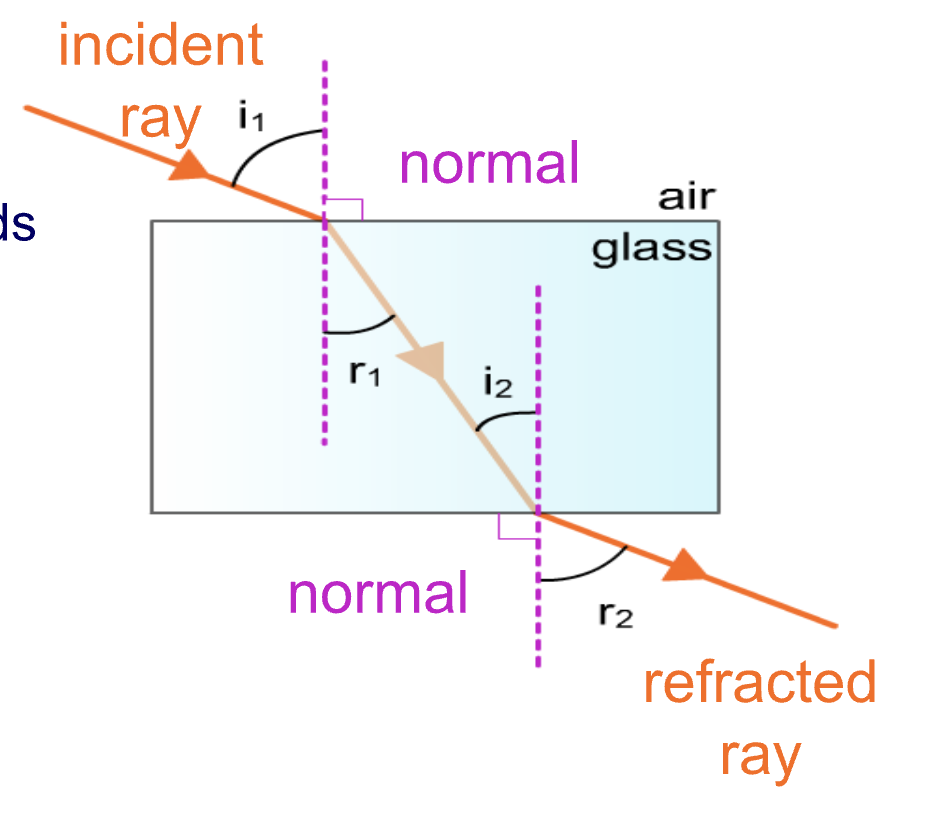
more or less dense medium

more = light ray slows down, sound speeds up (away ffrom normal)

less = light ray speeds up, sound slows down, (towards normal

dispersion

process of white light splitting into its constituent colours

the angle of refraction is dependent on the wavelength of light. if red and blue light pass through a glass box the blue will refract more , causing colors to disperse.

however red will diffract more, and blue less

this is how rainbows are formed as light is refracted by the raindrops

what is the cirtical angle

the angle of incidence beyond which rays of light passing through a denser medium to the surface of a less dense medium are no longer refracted but totally reflected.

the critical angle is the minimal angel of incidence from a more dense to less dense medium to the angle of refraction is 90

t angles greater than the critical angle the light is totally internally reflected

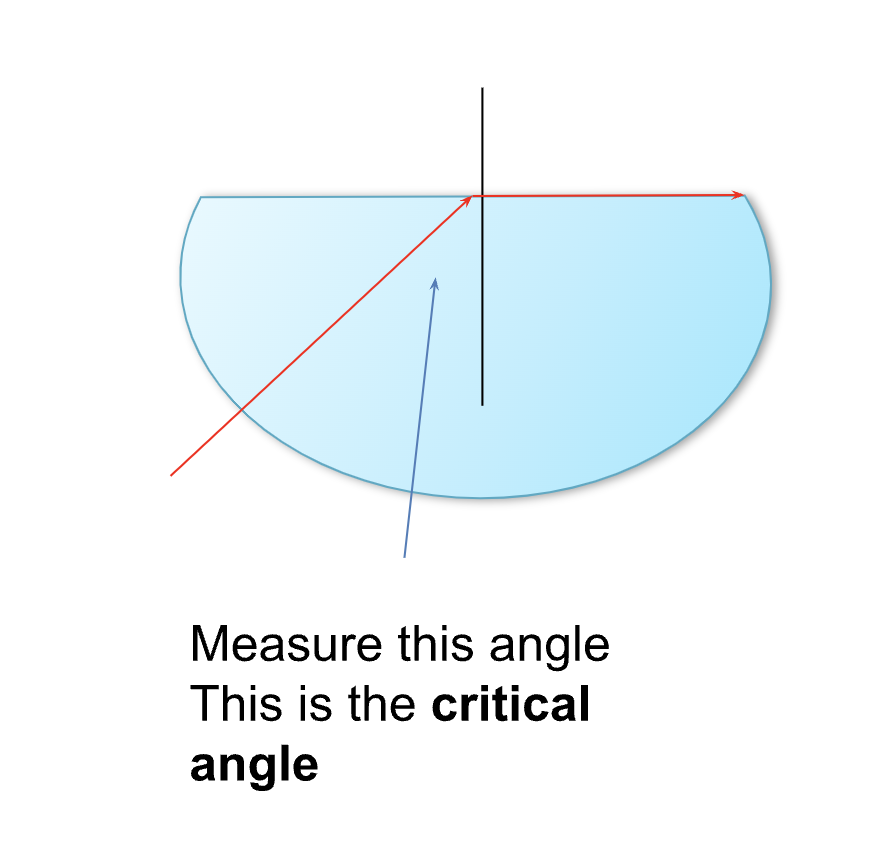
total internal reflection

requirements:

• the incident angle has to be higher than critical angle

• needs to go from more to less dense medium

there is always going to be some reflection however it only gets brighter when going past the critical angle

what happens to light as it passes through a slit

it diffracts causing interference patterns, with light and dark bands

the wave will propagate

how to find intensity after difraction

the resultant intensity at a point in front of the slit is found by summing all wavelets. this is hard since all wavelets travel a different distance, thus are out of phase with each other, if out of phase destructive interference causing a dark area, constructive will create maxima

to simplify this use a point far away from slit which makes wavelengths almost parallel

intensity is proportional to amp²

central maxima

occurs directly ahead of slit. it is far away as the wavelets are parallel travelled same distance thus in phase therefore their interference is constructive to give a region of high intensity and brightness

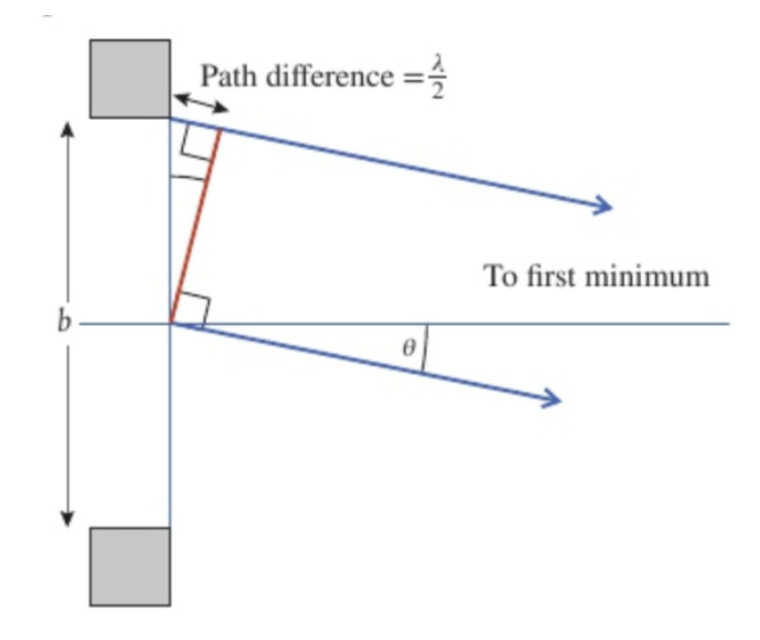
first minimum

they are travelling at an angle so they do not travel same distance. the wavelet at top will transfer further than at bottom, when these wavelets add together they have a destructive interference pattern due to them being out of phase to each other, to form region of low intensity

to calculate angle at which first minimum is formed

split the slit into two halves top and bottom if all wavelets form the top half cancel out all wavelets from the bottom the result will be dark region

to cancel the path difference must be 180

the angle is the angle the orange line makes, angle = lambda/ b

red and blue diffraction

red detracts most and blue least

double slit interference

light from single-slit interference is split in two by parallel narrow slits, and the light diffracts, creating an overlapping region where interference takes place.

this results in a series of light and dark regions called fringes

amplitude is changed with a varying intensity of fringes

from single slit to double the maxima will double in intensity and away from maxima will decrease in intensity

fringes

maximums

distance between fringes are the same measured to find an average

s = (λD)/ d

s = distance between maximums

D = distance from the slit to fringe

d = distance between slits

if the slit width increases less of a spread of diffraction, if it is less then width between fringes will increase

graph of single and double slit

a = single slit

b =double

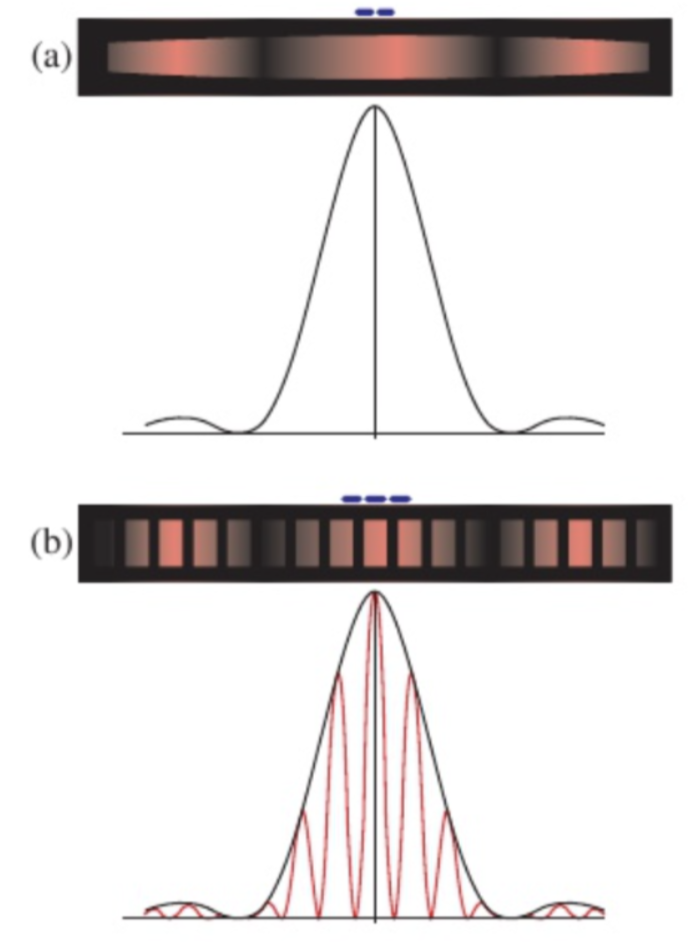
diffraction grating

d sin = n λ

d = distance between slits of diffraction

n = order of maxima, n = 0 central maxima

to find d, when given diffraction per millimeter, 0.01 m 750, if 750 lines per 1cm

what do we know about travelling waves

• transfer energy from one point to another

• no permanent displacement of particles of the medium

• two main types of waves are mechanical and emf

• a wave can be transverse or longitudinal depending on direction of oscillation

  • mechanical = sound = longitudinal

• displacement of particles s the distance moved form equilibrium

• amplitude is max displacement

• wavelength is length of one complete wave. distance between two points in same phase

• time period, how long for one wavelength

• number of waves in one sec

how are standing waves creates

two waves identical in wavelength, amplitude, and wave speed travel in opposite directions.

• when peak and trough superimpose they cancel

• when peak and peak super impose they double in amplitude

• further the peaks and troughs super impose again and destruct whole eave

• peak and peak meet and again enw amp

this process shows that the peaks always meet at same place

points between nodes are in phase with each other, either side of a node has phase difference of pi

no energy is transmitted rather the energy is stored

antinode and node

antinode is max

node is equilibrium no displacement, all points beiltween two nodes osciate in place

1st harmonic

string =

• 2 nodes 1 antinode

• ½ λ

open pipe

• 2 antinodes 1 node

• ½ λ

closed one end pipe

• 1 node 1 antinode

• ¼ λ

2nd harmonic

string

• 3 nodes 2 antinodes

• λ

open pipe

• 3 antinodes 2 nodes

• λ

closed one end pipe, atually 3rd

• 2 nodes 2 antinodes

• ¾ λ

3rd harmonic

string

• 4 nodes 3 antinodes

• 3/2 λ

open pipe

• 3 nodes 4 antinodes

• 3/2 λ

closed one end pipe - actaully the fifth harmonic

• 3 nodes 3 antinodes

• 5/4 λ

standing vs travelling = amp

standing:

• depends on position in relation to antinode

travelling:

• all points will oscillate at the amplitude at one time

standing vs travelling = frequency

standing:

• all points oscillate with same frequency

travelling:

• all points oscillate with same frequency

standing vs travelling = wavelengths

standing:

• twice the distance between two nodes or antinodes

travelling:

• distance between two points in phase with each other

standing vs travelling = phase

standing:

• all points between two nodes are in phase

travelling:

• all points within one wavelength have different phases

standing vs travelling = energy

standing:

• has EK but do snot transfer

travelling:

• transfers energy

oscilate

displacement changes over time

displacement x = acoswt

w is the angular frequency, 2pif where f is the natural frequency

this can change by m or k

natural oscillation/ frequency

f = squareroot (k/m) divided by 2 pi

the frequency at which a system oscillates when not subjected to a continuous or repeated external force.

opposing force in spring in fluid

if we now add fluid around ball it will experience viscous force opposing its motion. Taking away energy

this force is proportional to the velocity of the ball so

equation

amplitude changes exponentially with time

b = constant of proportionality relating the drag force to velocity

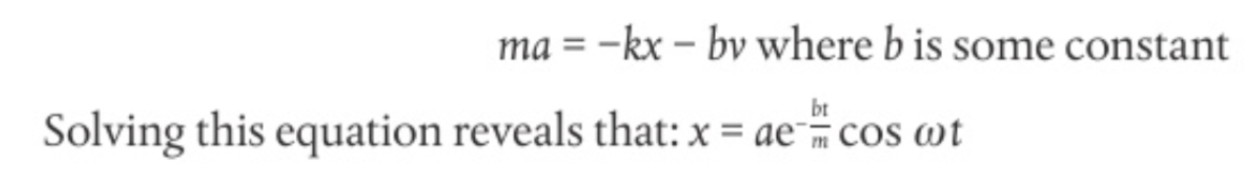
over damped

the system tends towards the equilibrium slowly

but never moves through equilibrium

critically damped

the mass returns to the equilibrium position as quickly as possible without crossing it is all energy is gone and just stop s

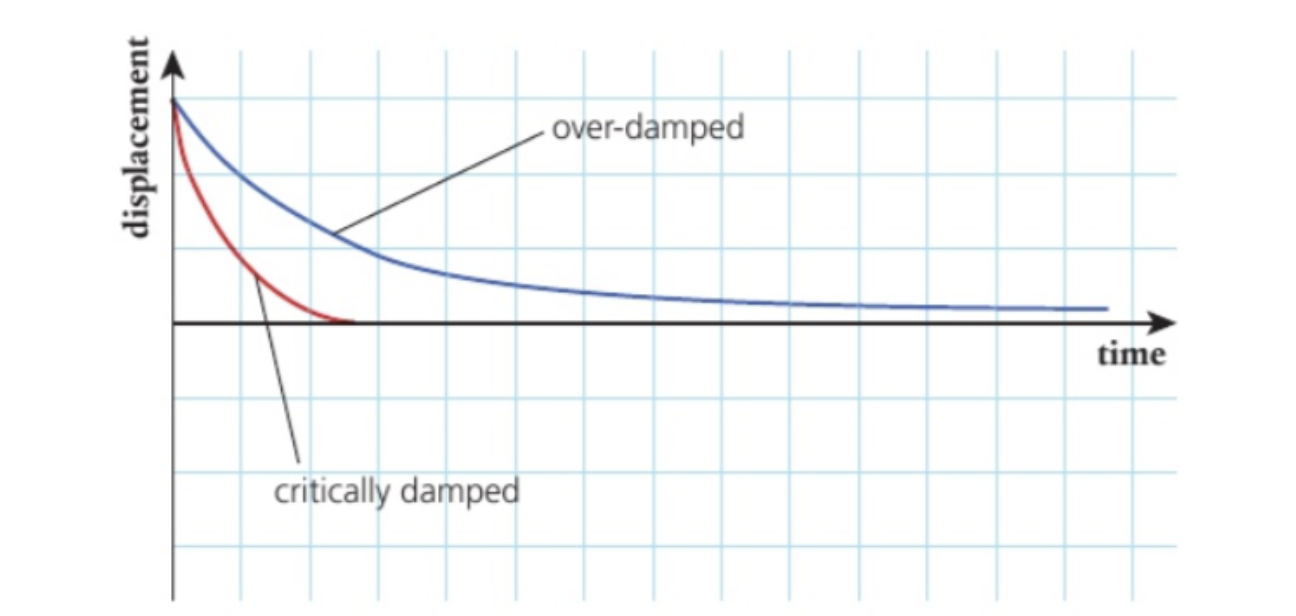
damping

the loss of energy of an oscillating system by dissipation.

forced vibration

is an oscillating system is disturbed it oscillates at its natural frequency. the mass can vibrate at other frequencies by applying a siussiodally varying force, then energy is transferred from the motor driving the oscillating platform to the ball and spring, thus it oscillates with frequency of driver

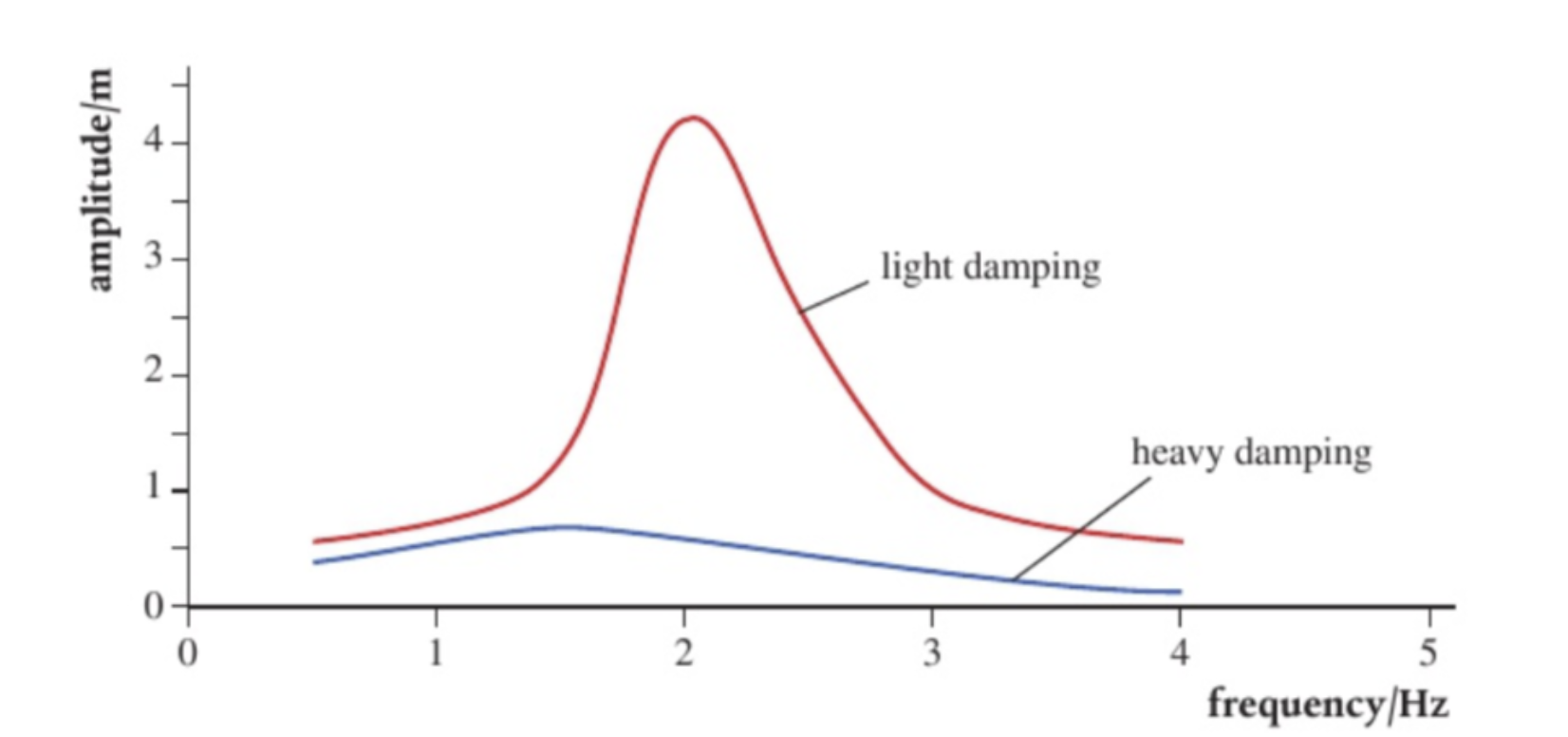
resonance

when driving frequency equals the natural frequency

creating largest possible amplitude

if not at natural frequency then amplitude is smaller

light and heavy damping with an example

when damping oscillator is driven, energy supplied by driver is providing energy to drive the system plus doing work against damping force.

daping reduces the max amplitude and resonate frequency of resonating system

they both go through equilibrium

a tall buildong

can collapse if its natural frequency matches the frequency of the earthquake

Doppler effect

changed in observed/apparent frequency when there is relative motion between the observer and the source

doppler effect graph

circles are the wavefronts

source moving to stationary observer apparent frequency increases

intensity increases closer to the source as it is louder, velocity of sound changes relative to the observer, velocity of sound is relative to air, thus moving closer toward soundv elocity will increase

doppler equations

moving source: + = source moving away smaller frequency thus greater wavelength

moving observer: - observer moving away, smaller frequency thus greater wavelength

doppler in EMF radiation

Δ F = (v/c)F₀

Δ F = change in frequency

v = relative speed of source of observer

c = speed of light in vacuum

F₀ = original frequency

red shift

If light is moving away from us, it will have a loner freuncy and be observed as red change of wavelength

This is used to calculate how fast stars are moving away from us, if frequency decreases it goes away from us, as the sound goes slower longer wavelength

hubble’s constant

how fast the universe is expanding

v = Hd

v = recessional velocity, how fast moving away

d = distance travelled

v/c = Δλ/λ = z

v = recessional velocity, how fast moving away

c = speed of light

z = fractional increase no units: the red shift

there is a linear relationship between recessional velocity and distance to galaxy, further away a galaxy is the faster it moves away from us

refraction

the change of direction of propagation, when passing from one medium to another

the frequency of waves don’t change when the wave slows down, thus wavelength must be shorter

sound wave moving through air to water

the sound wave speeds up, to sound the water is less dense this is because sound wave is longitudinal wave, thus the particles collide more,

what remains constant fro a wave to travel through a medium

frequency

single slit and slit width effect

narow slit, broader central maxima but less intensity

wider slit, narrow central maxima and greater intensity

width of diffraction maximum meaning

the width of the central maxima, we can divide this value by two to find the distance to first minima, as the width for teh diffarction maxima takes from both sides, we only need from 1 side of n = 0

how are standing waves created

Standing waves are formed by the superposition of two identical waves traveling in opposite directions. These waves interfere constructively and destructively to create regions of maximum displacement (antinodes) and zero displacement (nodes). Nodes are points of zero displacement where destructive interference occurs. Antinodes are points of maximum displacement where constructive interference occurs.