From the universe to the atoms

The Big Bang Theory

The universe has a hot and dense beginning and has been expanding ever since.

Creation and separation of fundamental forces

• Gravitational force separated first

• Strong nuclear force separated from electromagnetic and weak nuclear force

Began 13-8 billion years ago.

7 stages of Big Bang

1. The big bang event and inflation - singularity. Mostly made of radiation which far exceeded the amount of matter.

2. Hot soup of electrons, photons, and subatomic particles

3. Nucleons from (protons & neutrons)

4. Nuclei form (but no atom yet), and universe is too hot for light to shine without scattering. —> Nucleosynthesis

5. Atoms finally form (mostly hydrogen and helium) and light can shine freely

6. Accretion - Gravity pulls the atom into stars and galaxies

7. Present day

Accretion

The process by which denser objects attract nearby matter due to their gravity.

1. Matter is unevenly spread across the universe.

2. Gravity is stronger in denser areas.

3. Mass gathers in these regions, forming large gas clouds.

4. Gas clouds are uneven inside, causing smaller dense areas.

5. These areas collapse under gravity, heating up.

6. Stars form from the hot, dense clumps.

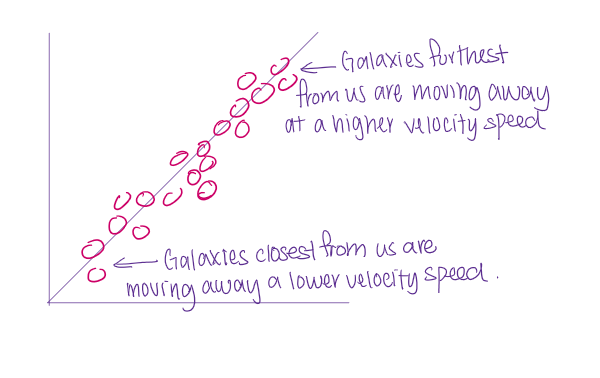
Hubble’s law - BBT evidence 

Hubble’s constant (H) = gradient of the line

• inverse of gradient = value of time (estimation of age of universe)

v= H_od

V = recession velocity

Observational proof that the universe was expanding: He measured the velocities of galaxies using the Doppler shifts in their spectra.

• Galaxies furthest from us are moving away at a higher velocity speed

• Galaxies closest from us are moving at a lower velocity speed.

Matter and Anti-matter

• particles are always created in pairs

• For every matter there is an antimatter particle

• At the instant they form and because they are so close tgt, they immediately annihilate each other and convert to pure energy.

Baryogenesis

During the rapid expansion and cooling of the universe, slightly more matter was created than antimatter. 

This is why most of the universe that we detect and observe is now matter. 

Baryonic assymmetry —> Ratio between matter : radiation ratio increases. Excess particle due to shortage of anti-particle were unable to convert into radiation 

Fundamental forces in BBT

• gravitational

• electromagnetic

• strong and weak nuclear forces

The particles which meditate these forces are known as field particles

Helium and hydrogen ratio - BBT evidence

In BBT the ratio of hydrogen to helium is 3:1. As the oldest gas clouds match this.

Matches the composition of the universe: 75% hydrogen and 25% helium

Explains the abundance of hydrogen and helium - can be only formed by nuclear fusion rxn in the centre of the stars.

Lithium also present

BBT evidence - cosmic microwave background radiation (cmbr) /afterglow

• After the big bang, the universe began to cool, after 300000 years the universe was sufficiently cool enough for radiation to able to travel through space for the first time.

• The heat radiated from this point in time as gamma rays but since the universe has expanded the radiation is now detected as microwave rays. - RED SHIFT 

• Explains not only that all masses began as dense form and been expanded infinitely since then, but it can determine the time of explosion.

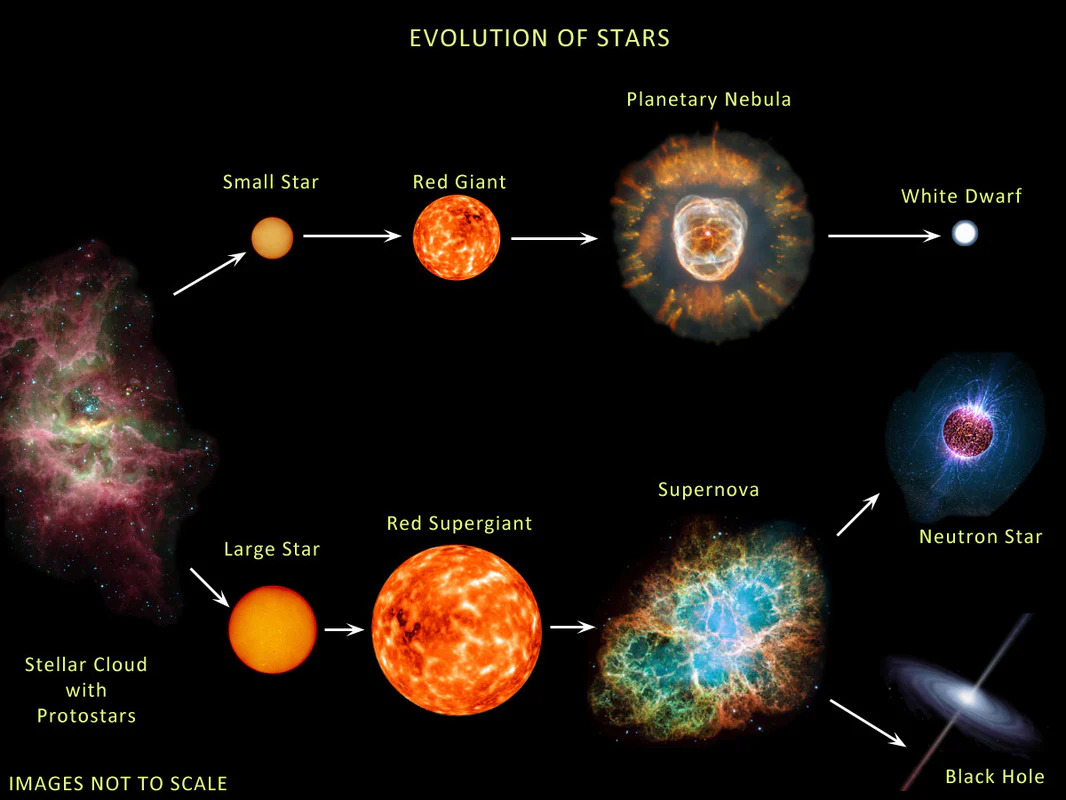
Lifecycle of star

Nucleosynthesis/fusion for each star

stars produce energy via nuclear fusion.

Process in which atomic nuclei physically combine to form one or more diff atomic nucleus and additional sub-atomic particles such as neutron.

Obey energy-mass conversation but requires the application of energy-mass equivalence.

proton-proton chain (fusing H to HE)

Stars with the same or smaller mass than our sun will produce energy by fusing protons to obtain Helium nuclei in the chain reaction

In the process, energy is released. The product therefore has less mass than the sum of the reactants, according to E = mc2.

• most common in main sequence

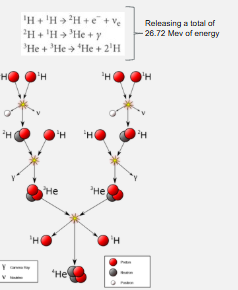
Proton-proton chain step

1. Two protons fuse to produce 2H nucleus

2. 2H nucleus fuses with a proton to produce 3He nucleus

3. two 3He nuclei fuse to produce 4He nucleus and two protons 

proton-proton chain and CNO reaction equation

3 gamma for CNO 

2 gamma for PP

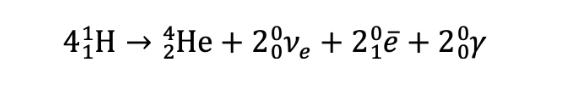
CNO reaction equation 

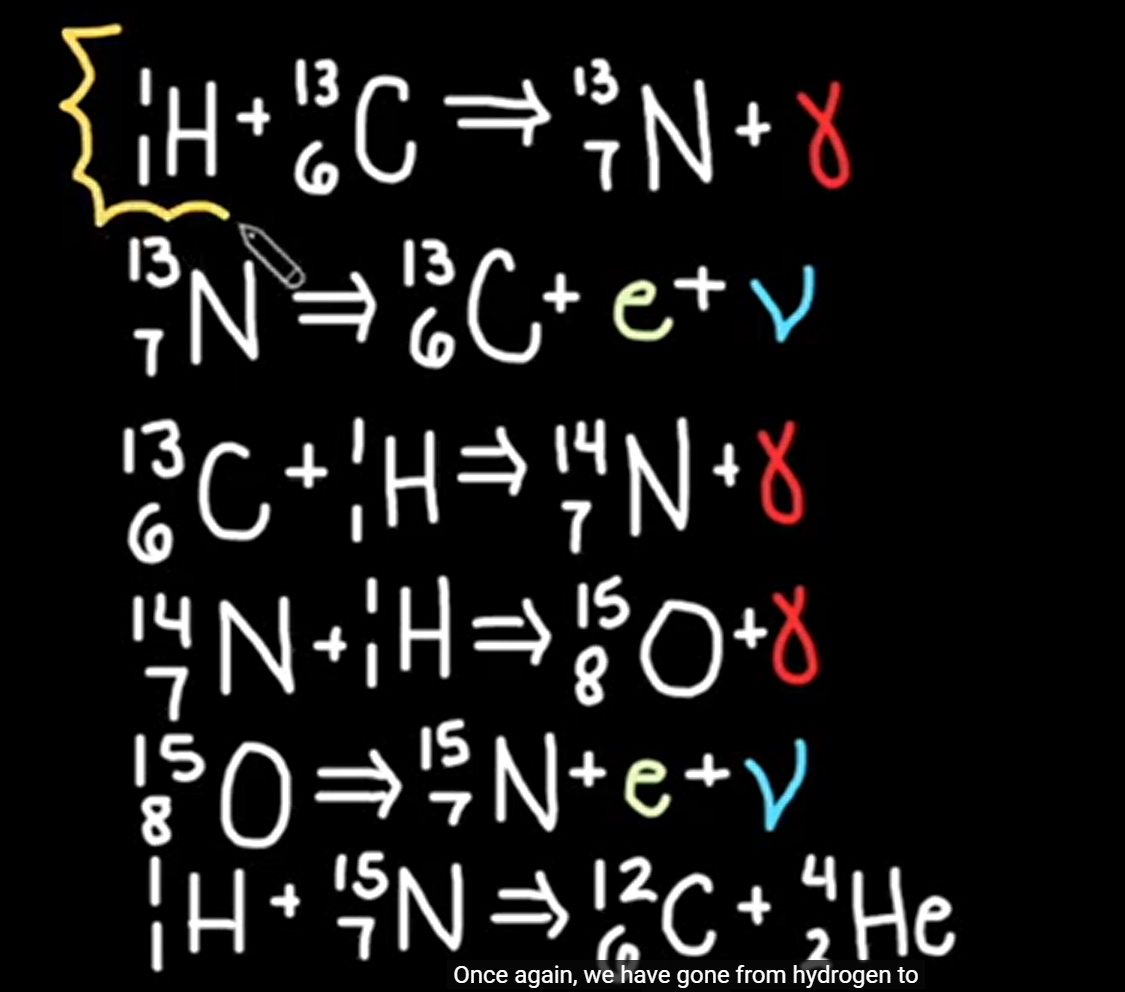
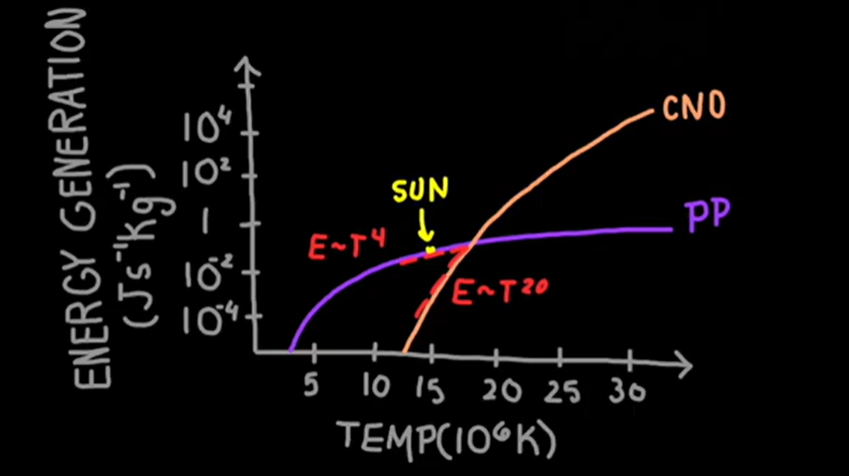
energy generation vs temp curve between CNO AND PP

The nuclei involved in the CNO cycle experience greater electrostatic repulsion due to their greater charge.

A higher core temperature is required so these nuclei have sufficient kinetic energy to overcome the repulsion and collide to undergo nuclear fusion. 

carbon-nitrogen oxygen cycle (CNO)

Carbon acts as a catalyst in the reaction as it transforms into nitrogen and then oxygen before returning back to carbon to start the cycle again.

• More common in supergiants

• 4 protons join the cycle to produce a 4He nucleus 

Main sequence star

• vary greatly in luminosity, mass, size, and surface temperature.

• TOP LEFT = heavier, larger, more luminous and higher surface temp

  • turn to super giants - consume their fuel very quickly.

• BOTTOM RIGHT = light, smaller, less luminous, lower surface temp

  • Turn to red giants - consume fuel very slowly and star as main star for a very long time

Red giant

• evolve from smaller main-sequence stars when they deplete their hydrogen source for nuclear fusions.

• Outer layers of gases expand due to higher temp

• Larger surface area compared to preceding main-sequence

Super giant

• Evolve from larger main-sequence stars when their hydrogen source are depleted.

• Greater surface and area

• However, due to their much larger surface area, the intensity of radiation is relatively low at the surfaces of super giants.

• Relatively low surface temp despite their great luminosity

White dwarfs

• the final stage of evolution following a red giant

• there are no more nuclei remaining for nuclear fusion

• when nuclear fusion cannot longer occur, the star contracts under the influence of gravitational force.

• They shed their outer layer exposing their core which increases temp

H-R diagram

Graphs the luminosity of stars against their surface temp. Matching luminosity and surface temp helps to determine the size/mass of a star.

A star in a particular region of a H-R diagram depends on its evolutionary stage. These stages are controlled by the nucleosynthesis rxn occuring in the star’s core.

Charged particle properties of Cathodes

• deflected by electric and mag field

• ray carries energy and momentum

  • attracted to positive charge

Electromagnetic wave properties of cathode ray

• identical, regardless of material used

• It emanates from the cathode and travel in a straight line

• would cast a shadow of solid object

• could penetrate thin metal foils

Maltese Cross experiment - cathode ray

What was done: An anode in the shape of a maltese cross was placed in the path of cathode ray.

Observation: A shadow of maltese cross was formed directly behind anode.

Conclusion: Cathode rays travel in a straight line and can cast a shadow.

Cathode ray containing electric and magnetic field experiment

What was done: A metal plate coated with fluorescent material was used to visualise the trajectory of a cathode ray. The cathode ray was passed through a uniform electric and mag field.

Observation: In the presence of an electric field, the path of the cathode ray was deflected in a direction that was consistent with a negatively charged mass.

Conclusion: Cathode rays are stream of negatively charged magnetic particles.

Paddle wheel

What was done: A glass paddle wheel that could move and rotate freely was placed in the path of cathode ray.

Observation: When the glass paddle wheel was struck by a cathode ray, it rotated and moved towards the cathode ray.

Conclusion: Cathode rays have momentum and kinetic energy - they have mass and are particles in nature.

Thomson’s charge-to-mass experiment

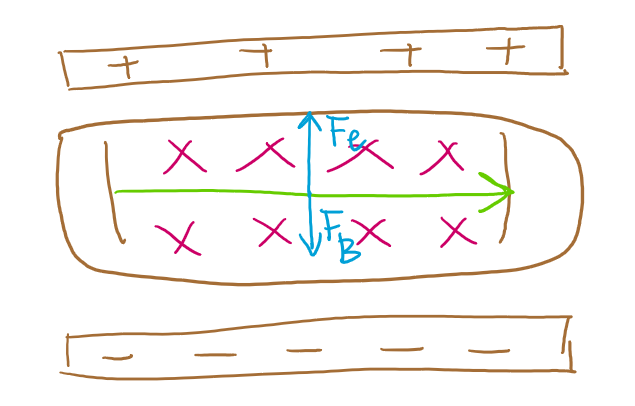
A pair of charged metal plates was used to create a uniform electric field. When a cathode ray travels through this field, it was deflected towards a positive field.

Next Thomson applied a uniform magnetic field using current-carrying coils. The direction o f this magnetic field was perpendicular to the electric field and positioned such that it would cause the cathode ray to deflect downwards.

The mathematical calculation for Thomson’s charge-to-mass experiment

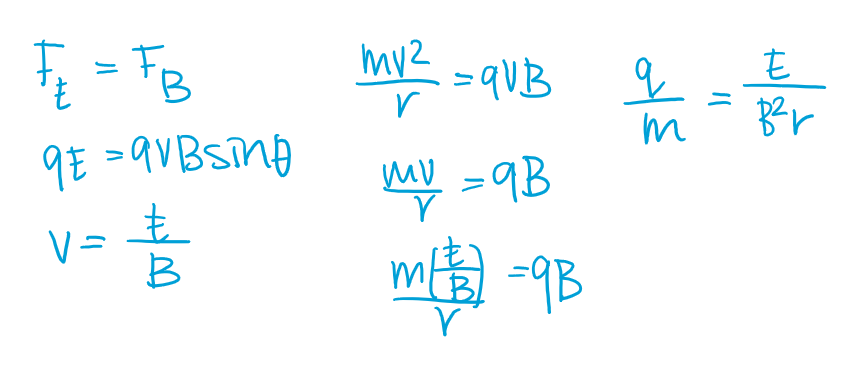
Thomson’s interpretation of his charge-to-mass experiment

Proved cathode rays have mass and a negative charge, identifying them as electrons. their constant charge-to-mass ratio across all materials proved they are fundamental to all matter. Their ratio being 1800x greater than hydrogen ions implied electrons are 1800x lighter.

Thomson’s ‘plum pudding’ model

Negatively charged electrons are dispersed in a positive mass due to electrostatic repulsion. The electrons are held together in the atom due to their attraction to the positive mass.

Limitations: Lack of explanation for the positive mass.

Milikan’s Oil experiment

Millikan sprayed tiny oil droplets into a chamber between two charged plates. As the droplets passed through the spray nozzle, they gained charge from friction. When a voltage was applied across the plates, the electric force on the charged droplets could balance their weight, causing some droplets to remain suspended in mid-air.

Charge is quantised - milikan’s oil experiment

• Discovered that some oil drops required a higher voltage to be applied in order for them to be suspended between the plates.

• This was due to the oil drop picking up extra charge as it came out of the spray nozzle.

• Concluded that when he calculate the charge he always got a multiple of 1.6×10-19C

Milikan Oil Experiment - Mathematical calculation

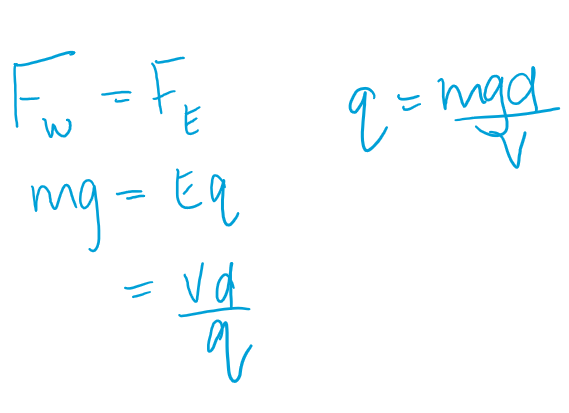
Geiger-Marsden Experiment

Fired alpha particles at a thin gold foil. The gold foil was surrounded by a screen that would cause scintillations when alpha particles hit it.

Geiger-Marsden Experiment Observations

• Most alpha particles went through undeflected as most scintillations were observed directly behind the gold foil. Supported Rutherford’s postulate that an atom is mostly empty space.

• Few alpha particles were deflected and some were reflected back. Supported the presence of a region in the atom of highly positive charge (nucleus). In an atom of gold, the charge and mass of the nucleus are substantially greater than that of an alpha particle. As a result, when an alpha particle collided with the nucleus it was reflected.

Why can’t JJ Thomson explain: Geiger-Marsden Experiment

its dispersed positive charge could not explain the significant deflections of alpha particles observed in the gold-foil experiment

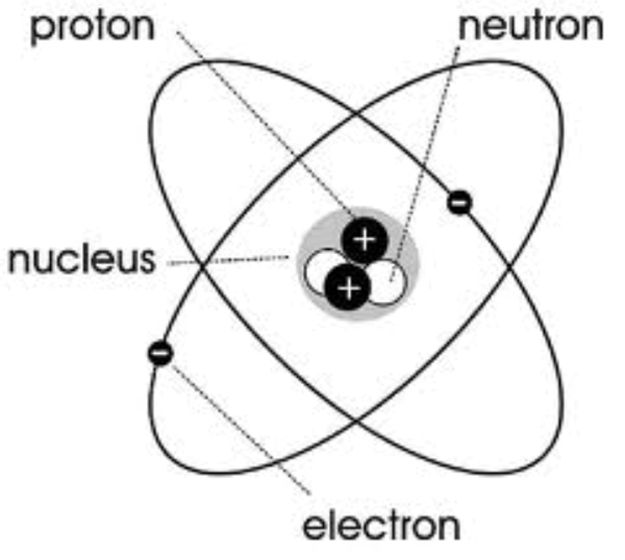
Rutherford’s model of an atom

• nucleus = a highly concentrated positively charged region in the centre of the atom

• Most of the atom is empty space

• Electrons orbit with the nucleus

Rutherford’s proton discovery

Fired alpha particles at a sample of nitrogen gas which resulted in a transmutation rxn producing protons.

Conducted similar experiment to Thomson's to determine the value of the charge to mass ratio of a proton. Showed that a proton is positively charged and much heavier than an electron.

Limitation of Rutherford’s model

•He could not explain what exactly was inside the nucleus. The number of protons were less than the atomic mass. This led to the speculation that there is something else inside the atom that scientists weren’t aware of.

•Did not know how the electrons were arranged around the nucleus.

•Could not explain how electrons did not collapse into positive charges.

•Electrons are moving= moving objects have centripetal acceleration and ccelerating charges produce EMR (energy), which should lead to loss of energy.

•Therefore, every atom should be unstable and short lived. But it isn’t!

Chadwick’s discovery of neutron

Alpha particles were fired at berylium and unknown particles were observed coming out of the berylium.

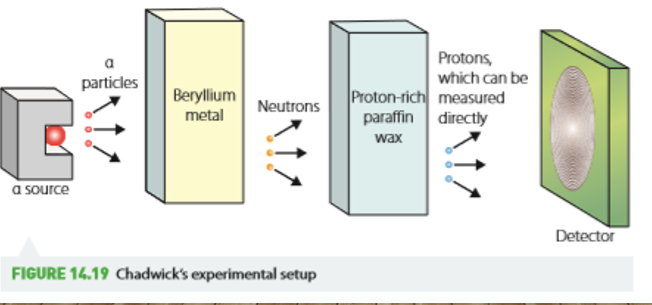
Conclusions of chadwick’s discovery

• same mass as protons

• Neutrally charged

Limitation of Chadwick

He had the same problem as Rutherford when it came to electrons.

• did not know how electrons were arranged around the nucleus

• Could not explain how electrons did not collapse into positive charge.

Chadwick’s model diagram

Bohr’s postulate

1.An electron moves in circular orbit around the nucleus. (Electrostatic attraction provides centripetal force.)

2.Electrons can only exist in particular energy levels and orbits. When an electron is in a stable orbit, it will not emit or absorb energy.

3.When an electron moves into a different orbit, energy will be absorbed or emitted . The energy absorbed or emitted will relate to the energy difference between the shells according to: E = hf

4.The angular momentum of electrons is quantized.

Problems with Bohr’s mdoel

1. it was a mixture of classical and quantum physics.

  2. it could not explain the Zeeman effect (when an external magnetic field interacts with the electron’s energy state.)

  3. it could not explain the variable intensity/brightness of the spectral lines. (the probabilities need quantum modelling)

  4. it could not account for the hyperfine spectral lines (the magnetic field of the nucleus interacts with the electron’s magnetic properties).

  5. it only worked for hydrogen and not larger atoms.

The Balmer series + formula

The hydrogen spectrum consists of a series which correspond to specific colours and wvaelengths. These are described as discrete, single line spectra

Electrons relationship to energy

Schrodinger’s contribution to the atomic model

He used de Brogile’s wave idea and developed a complex mathematical equation to describe electron behaviour within different energy shells. He described each electron ‘shell’ as a cloud of probability.

De Brogile’s matter wave duality

Bohr could not justify why electrons must be in fixed orbital shells.

He proposes that moving matter can exhibit wave particles according to the equation: λ = h/(mv)

This suggests that the wavelength is inversely proportional to its momentum.

Standing waves in De Brogile’s matter wave duality

He postulated that electrons orbit the nucleus as standing waves to justify the idea of fixed energy shells.

When electrons behave as standing waves, they no longer emit energy in the form of radiation. He provides an explanation for Bohr’s first postulate - electrons orbit the nucleus in ‘stationary states’ and do not emit energy.

Standing waves

Standing waves are formed as a result of the interference between two waves of equal frequency and amplitude travelling in opposite direction.

Experimental evidence for De Brogile’s theory

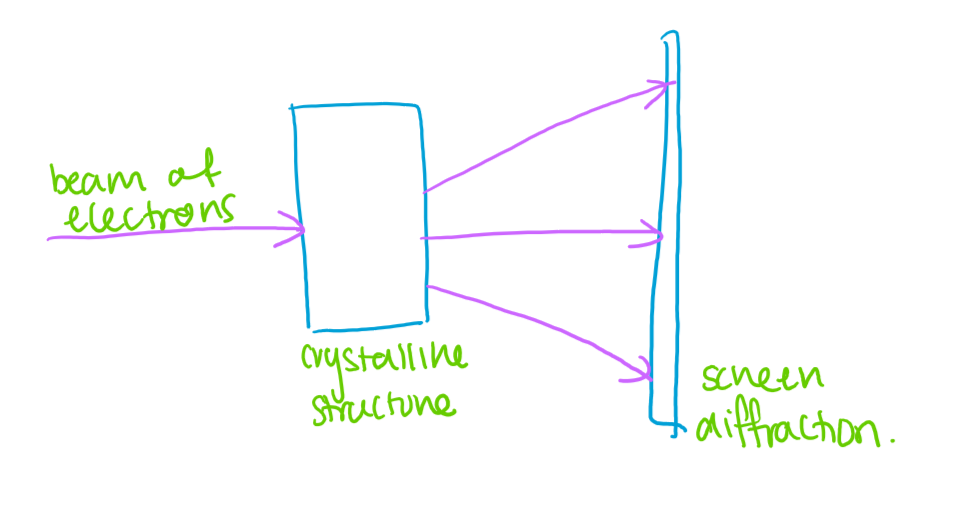
Davisson’s and Germer’s Nickel Crystal Experiment

A beam of electrons was produced and accelerated at a nickel crystal surfaced (lattice).

Observations:

• Instead of scattering randomly, the electrons show intensity peaks at certain angles.

• These peaks corresponded exactly to what would be expected if the electrons were behaving like waves undergoing attraction from the lattice.

Schrodinger’s contribution to the atomic model

He used de Brogile’s wave idea and developed a complex mathematical equation to describe electron behaviour within different energy shells. He describes each electron ‘shell’ as a cloud of probability.

Schrodinger - quantum numbers

Quantum number	Interpretation
Principle quantum no. N (shell)	No. of spherical nodes
Orbital quantum no. L (subshell)	Shape of orbital determine the s,p,d,f orbital shape
Organic magnetic quantum no. M1	Orientation of orbital shape.

Paulli Exclusion Principle

In an atom no two electrons can ever simultaneously occupy the same quantum state.

• Starts with the lowest energy state

How did Schrodinger explain the spectra of larger atoms?

The interaction between electrons can be accounted for in Schrodinger’s equation.

How did Schrodinger explain the relative intensity of spectral lines

This depends on the probability of a transition from one quantum state to another, which can be calculated correctly now that quantum states are understood.

How did Schrodinger explain the Zeeman effect

Explained by the mi quantum number.

Quantum states with a different value of Mi have different energy in the presence of a magnetic field, producing different spectral lines wavelength for transitions involving those states.

How did Schrodinger explain Hyperfine splitting

Explained by electron spin and the spin magnetic quantum no. Ms.

In certain atoms the 2 different electron spin states Ms = ±1/2 have slightly diff energies. This results in 2 slightly diff. spectral line wavelengths

Strong Nuclear Force

is a fundamental force acting between nucleons and is responsible for the stability of nuclei.

• This force represents the “glue” that holds the nucleons together and overcome the electrostatic repulsion.

Stability of a nucleus

Determined by the balance between electrostatic repulsive force, that exist between the protons and the nuclear strong force that attracts all nucleons together.

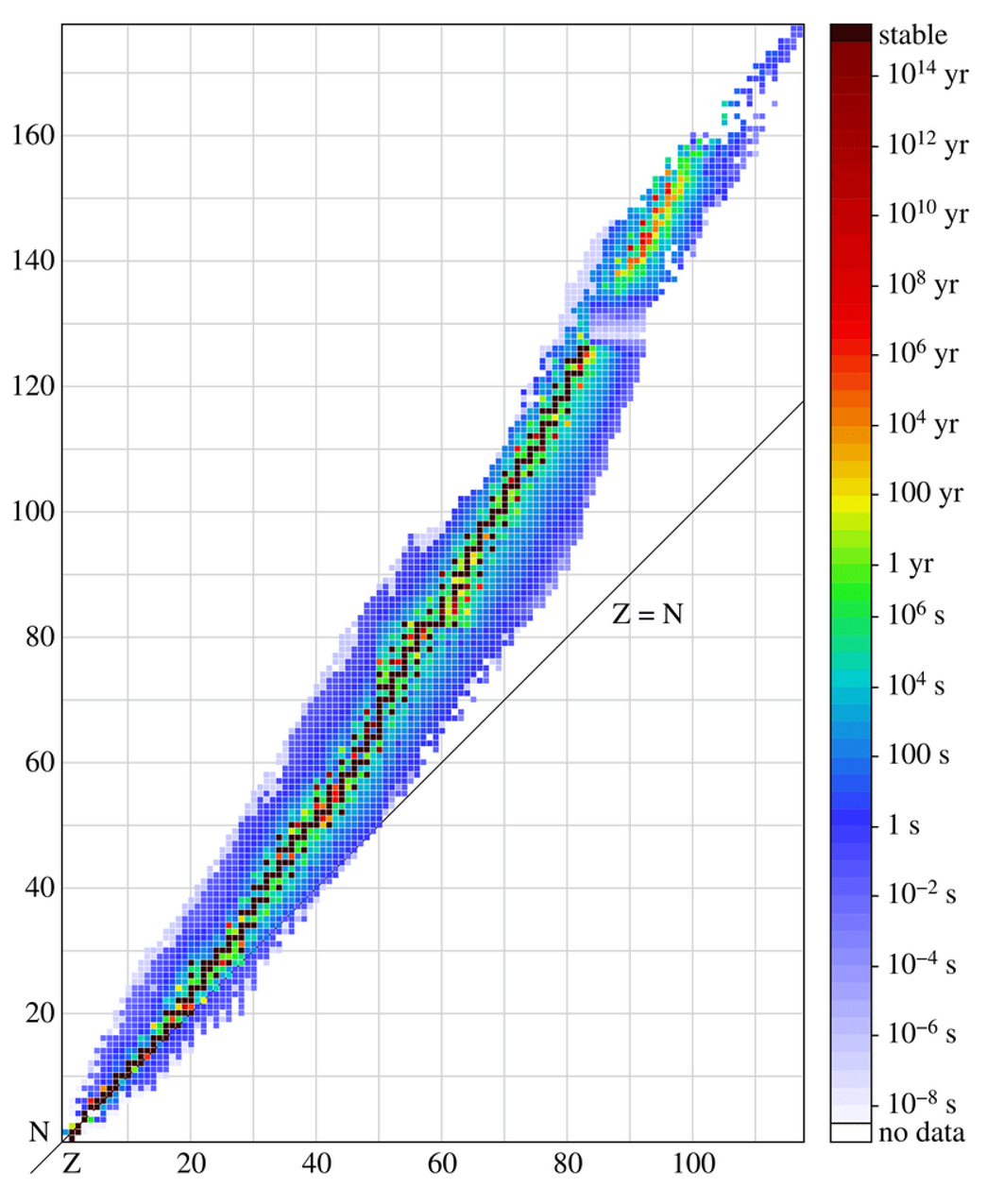
what does this graph represent?

Neutron-to-proton ratio - determining nuclear stability

• Protons inside the nucleus are all positively charged, so they repel each other due to electrostatic (Coulomb) repulsion.

• Neutrons do not carry charge but contribute to the strong nuclear force, which binds nucleons together at very short ranges.

• A stable nucleus requires the right balance between protons and neutrons:

  • Light nuclei (low mass numbers) are most stable when n:p≈1:1n:p \approx 1:1.

  • Heavier nuclei need more neutrons than protons (n:p>1n:p > 1) to counteract the stronger proton–proton repulsion. For example, stable isotopes of lead (Z=82Z = 82) have roughly n:p≈1.5n:p \approx 1.5.

• If the ratio deviates too far from the band of stability:

  • Too many neutrons → beta-minus decay (a neutron converts into a proton).

  • Too few neutrons → beta-plus decay or electron capture (a proton converts into a neutron).

The total no. of nucleons inside the the nucleus - determining nuclear stability

• The strong nuclear force is short-ranged, only binding neighbouring nucleons. As nuclei grow larger, each proton still experiences repulsion from all other protons, but the strong force cannot counterbalance this across the entire nucleus.

• When nucleons are packed too closely, the strong force becomes repulsive at extremely short distances, further destabilising the nucleus.

• Once the atomic number exceeds Z=83, the electrostatic repulsion between protons dominates, making almost all such isotopes unstable and prone to radioactive decay (alpha, beta, or spontaneous fission).

Why are elements smaller than iron less stable

Because they have a smaller no. of nucleons. The strong nuclear force is not large enough to overcome the electrostatic repulsion that exists between the protons in the nucleus.

Nucleons in a nucleus bound to each other - ENERGY

Have a negative potential energy + negative total energy

• decrease in energy when they become bound.

Binding energy

Defined as the total work required to overcome the strong force and separate its nucleus

Doing work on the nucleons will increase their total energy from the negative value they have as bond nucleons, to zero for a free stationary nucleon.

Corresponds to the mass defect by E=mc²

side with energy = more stable = less mass

The binding energy per nucleon

Is energy required to disassemble the nucleus into its constituents. The higher this value, the more energy required to pull the nucleons apart, meaning the nucleus is more tightly bound and more stable.

Nuclear transmutation

is a process of one element changing into another element through nuclear reactions.

• is when radioactive isotopes spontaneously decay and transform into more stable isotopes.

transmutation - radioactive decay

When atoms undergo nuclear decay, it is not normally single transmutations into a new species. An original “parent” atom undergoes a series of transmutations into new, radioactive “decay” elements ending finally with a daughter element that is stable.

Natural transmutation

The spontaneous breakdown of an isotope into a new isotope.

properties of alpha, beta, gamma decay

Properties	Alpha	Beta	Gamma
Speed	0.1c	0.9c	C
Penetration	Poor	0.5cm aluminium	10cm lead
Ionisation ability	High	Mid	Low

mass defect

is the difference between the mass of an object and the sum of the masses of its constituent particles

Applications of mass defect

1. Binding energy per nucleon

2. Transmutation rxn

3. Fusion + fission

Fission

Process of splitting a larger atomic nucleus into two or more stable nuclei

How can fission occur?

• spontaneously in unstable nuclei as an uncommon form of decay

• triggered by bonding particle

Example of fission rxn equation

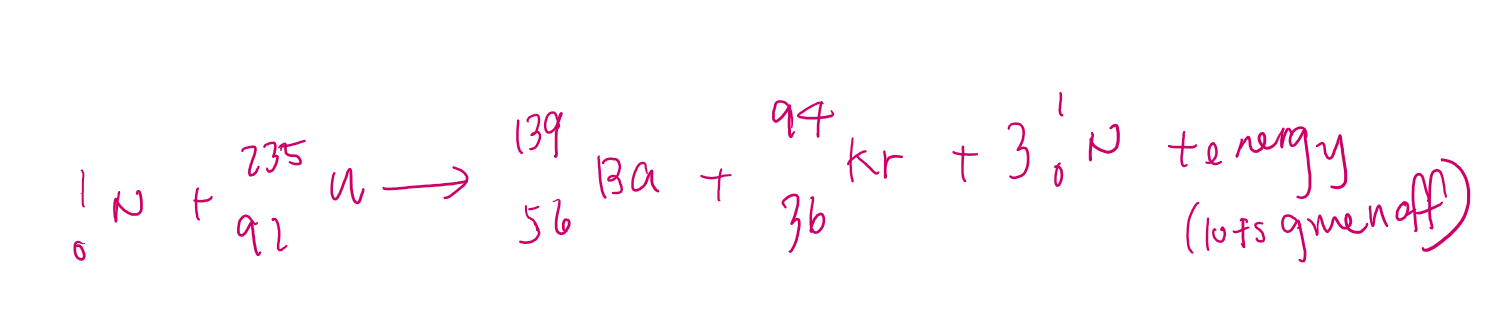
fission chain rxn

an uncontrolled nuclear rxn when one rxn generates 3 more rxns and this quickly escalates to an explosion

nuclear fission reactor diagram

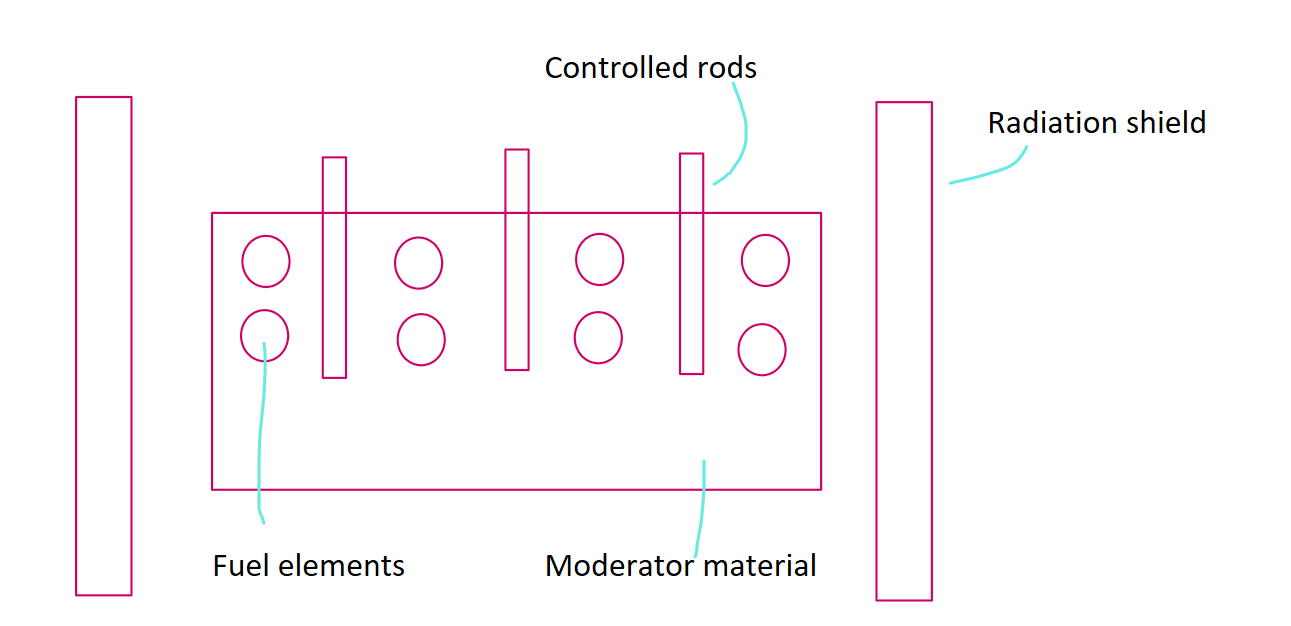
nuclear fission reactor components + function

core of fuel (U) = contains nuclei that are capable of undergoing fission when triggered. fissions to release energy and neutrons to maintain a nuclear chain rxn.

moderator = slows down neutrons to extract energy and make fission more likely

coolant = external thermal energy from the core

control rods = absorb neutrons to control reaction rate

radiation shield = prevents radiation and neutrons from escaping

energy and mass equivalence 

fusion

= the process by which lighter nuclei are joined together to form a larger nucleus

• binding energy per nucleon decreases as mass number decreases for nuclei with a mass lower than 60.

• smaller nucleus can release energy are they are joined tgt to form a larger nucleus

fusion rxn equation example

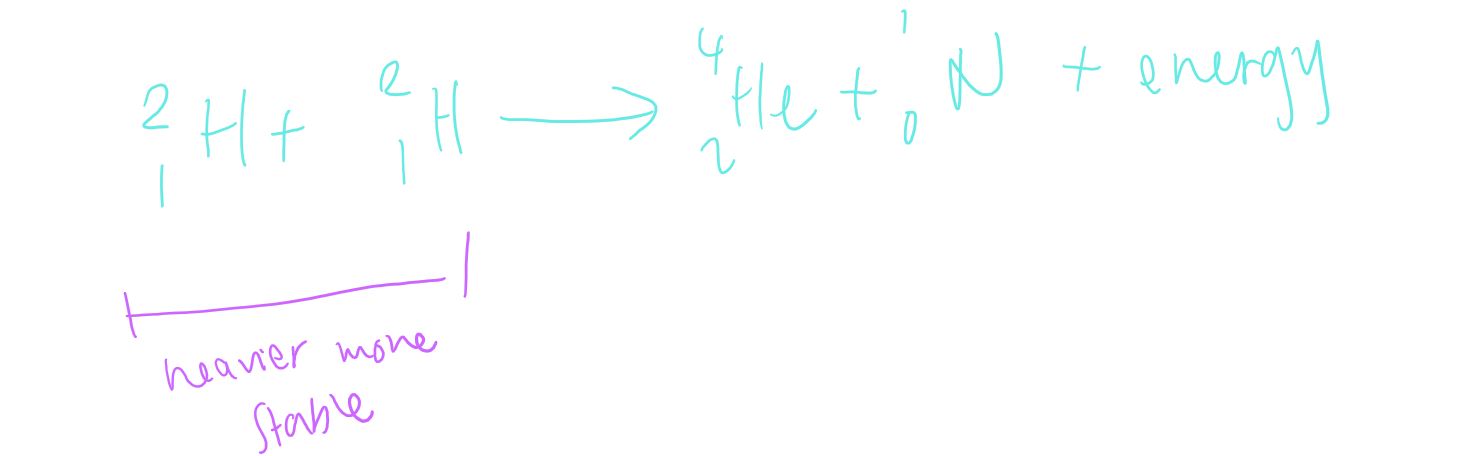
the standard model of matter

is a theory that explains our current understanding of the nature of matter by answering what the components of matter are and how the components interact with each other.

What are the three “families” of elementary particles

• 6 quarks

• 6 leptons

• 5 force carrier particles including the photon

• their anti-particles

Name of the 6 quarks

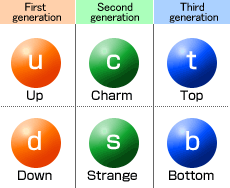
quarks

they are elementary particles which are usually found in combinations to form composite particles called hadrons such as protons and neutrons

Properties of quarks

• have fractional electric charge

  • up, charm, top charge = 2/3e

  • down, strange, bottom charge = -1/3 e

• Exists in groups with other quarks. they combine to make composite particles called hadrons which are held together by strong force.

• the only combination of quarks which can form hadrons must have a total integer charge.

the 2 common classes of hadrons

Baryons are any hadrons which are made of 3 quarks qqq or 3 antiquarks qqq

Mesons are any hadrons which are made of one quark and one antiquark qq

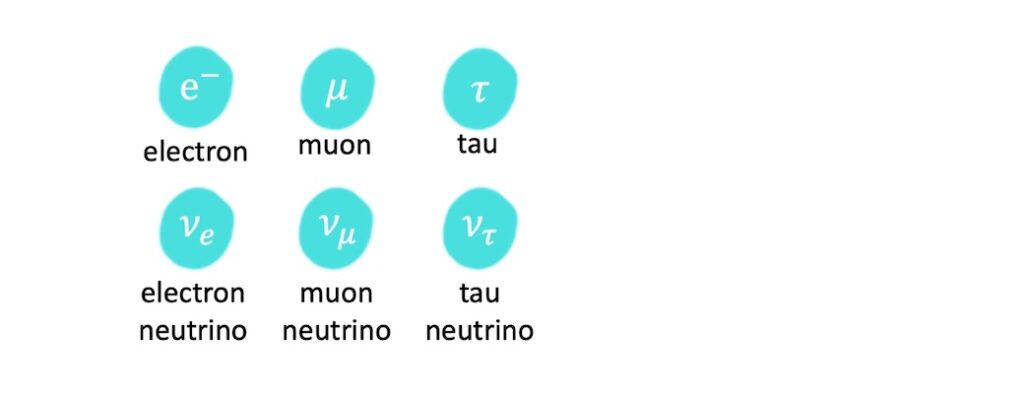
leptons

are a type of elementary particles that do not experience the strong force — cannot be held inside a nucleus

name of leptons

four carrier particles

all interactions between particles can be explained in terms of four fundamental forces which are meditated by force carrier particles or force carrier bosons

name of four carrier particles

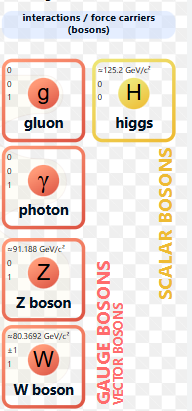
properties of four carrier particles

• these bosons exists as virtual particles which briefly come into existence and disappear.

• when a boson is exchanged between two matter particles, the corresponding force is “communicated” between them.

photon - four carrier particles

carries the electromagnetic force

• this force affects charges and currents

• virtual photons are not visible

gluon - four carries particles

carries the strong force

• this is short-range focus that holds quarks tgt.

• neighbouring nucleons which are made from quarks experience the residual strong force where they are close enough to still be in range

weak nuclear force

is meditated by the W+, W-,and Z^o

• this is not a conventional terms in terms of attraction and repulsion.

• instead it can change the charge and/or flavour of particles

• it is responsible for beta decay in which photons can turn into neutrons (vice versa)

particle accerator

devices used for accelerating elementary particles such as electrons and protons to high velocities and energies by means of electric or electromagnetic fields.

by colliding with targets or other accelerated particles, energy can be converted to mass and heavy, unstable particles can be studied.

two basic principles of particle accelerators

• electric field are used to accelerate the particles

• magnetic fields are used to steer the particles