PSYC 300 Module 15

Descriptive vs. Inferential Statistics

Descriptive vs. Inferential Statistics

Descriptive statistics: summarizes and describes data, cannot make generalizations or predictions about population

Inferential statistics: makes inferences from distributions, can make generalizations or predictions about population

The Normal Disribution

A common probability distribution of values of a continuous variable around the mean

Reading a Normal Distribution Graph (Curve)

- Middle values are mean=median=mode

- Frequency of values is on y-axis

- Scale of continuous variable on x-axis

- Spread determined by SD

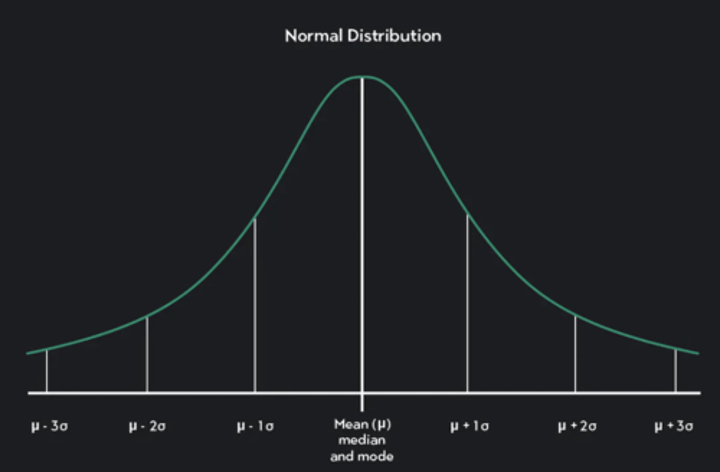
Properties of a Normal Distribution

1. Symmetrical

2. Unimodal (one peak)

3. Bell-shaped curve

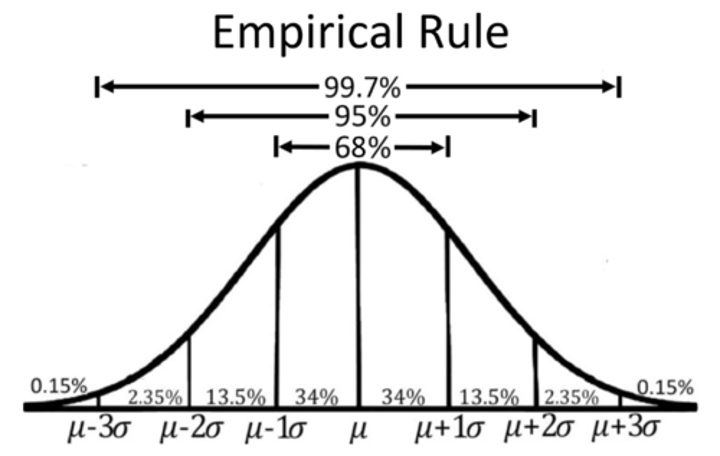
Empirical Rule (68-95-99.7 Rule)

- 68% of data lie within 1 SD of mean

- 95% of data lie within 2 SDs of mean

- 99.7% of data lie within 3 SDs of mean

- 0.30% of data lie within 4 SDs of mean

The Standard Normal Distribution

A normal distribution with a mean of 0 and a SD of 1

Properties of the Standard Normal Distribution

1. The cumulative area increases as the z-scores increase

3. The cumulative area is close to 0 for z-scores close to z=-3.49

4. The cumulative area is close to 1 for z-scores close to z=3.49

2. The cumulative area for z=0 is 0.5000 (50%)

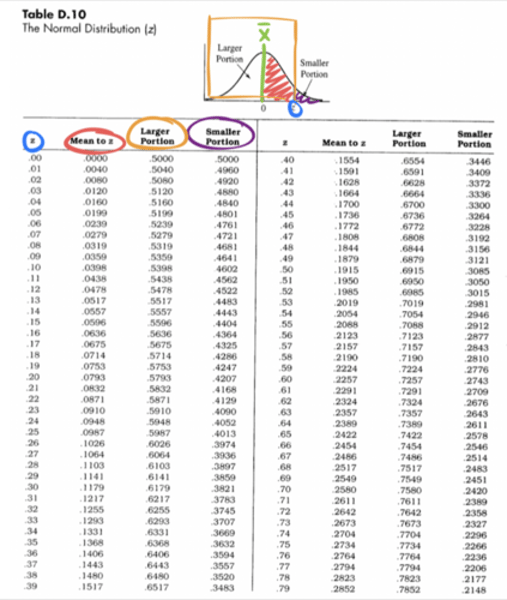
Reading a Z-Table

- Larger portion=area under the curve for positive z-values

- Smaller portion=area under the curve for negative z-scores

Standardization

- The process in which each data value of a normally distributed variable (x) is transformed into a z-score

- The result is the standard normal distribution

Standardization Formula

z=(x-μ)/σ

z=(value-mean)/std dev

How to convert z-scores to raw scores

x=μ+zσ

x=mean+(z-score)(std dev)